Quantum oscillations in a high-mobility electron gas
Over the past decade, many nonequilibrium phenomena have been discovered in high-mobility quantum Hall systems in a perpendicular magnetic field. For instance, microwave illumination of a two-dimensional electron gas leads to oscillations of the dissipative resistance with magnetic field (MIRO). When the microwave power is sufficiently strong, the net resistance in the minima of MIRO becomes vanishingly small, which has been attributed to electrical instability of a homogeneous state with negative absolute resistivity leading to a domain structure with zero net resistance.
MIRO originate from microwave-induced transitions between quantized Landau levels broadened by disorder. Such transitions should also lead to quantum magneto-oscillations in the absorption (QMA) of electromagnetic waves, as predicted more than thirty years ago by Ando and observed in low-mobility structures. Nevertheless, so far all attempts to detect QMA in high-mobility systems have been unsuccessful, despite the fact that dc transport measurements in the same samples revealed pronounced MIRO. The difficulty arises from the large metallic screening of microwaves by a high-mobility two-dimensional electron gas and also from absorption at magnetoplasmon resonances that mask QMA.
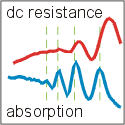
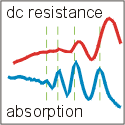
Now, in a paper appearing as a Rapid Communication in Physical Review B, Oleh Fedorych and colleagues in Grenoble, France, working with collaborators in Canada and Germany, have succeeded in simultaneous observation of QMA and MIRO in the same high-mobility quantum Hall system using a sensitive high-Q cavity technique. The observations are in a perfect agreement with a microscopic theoretical model that relates both types of oscillations to electron kinetics involving microwave-assisted inter- and intra-Landau level transitions. – Brad Rubin