Neighborly networks
Many networks, from the Internet to Facebook, are transitive: neighbors of the same node are probably neighbors of each other, or in social terms, your friends are likely to be friends with each other too. Apart from a few special cases, mathematically modeling such clustered networks is difficult and calculating their properties almost always requires numerical rather than analytical solutions. But as Mark Newman of the University of Michigan, US, reports in Physical Review Letters, it is in fact possible to generalize random graph models to include clustering in a way that allows exact derivations of network behavior.
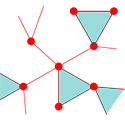
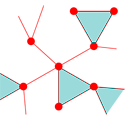
Conventional modeling of networks uses random configurations of vertices (nodes) in which the number of edges (connecting links) is specified for each vertex. Newman alters this by specifying how many triangles (the most elementary cluster consisting of three nodes) each vertex participates in, and how many single edges or “stubs” (apart from triangles) the vertex connects to. The network is then built out of triangles and stubs such that no edges or triangle corners are left hanging.
Constructing the network this way allows Newman to express the graph properties in the form of generating functions. These in turn allow derivation of such things as the “giant component” (the collection of nodes that can easily intercommunicate), the “small components” (the isolated groupings that are cut off from the rest of the nodes), and average path lengths from one node to another. Getting a handle on these characteristics should assist the analysis of real networks involved in the spread of disease, communications, and social interaction. – David Voss