Doping graphene into superconductivity
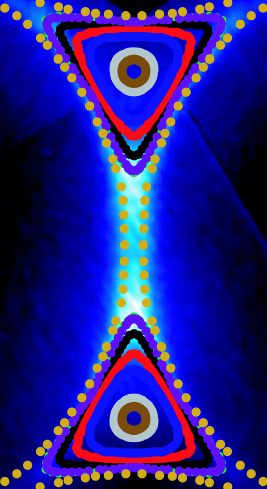
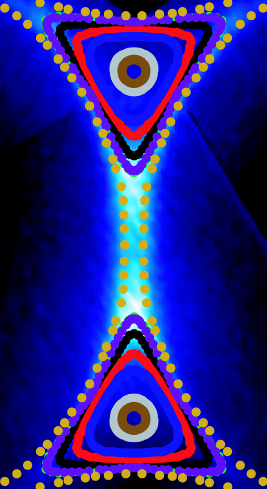
Graphene’s singular transport characteristics derive from its band structure, whose features include saddle points at the edges of the Brillouin zone that affect the topology of the Fermi surface.
In their article in Physical Review Letters, Jessica McChesney and her collaborators from the US, Germany, and Spain check for superconductivity in graphene because of a similarity—also caused by a saddle point in the band structure (a van Hove singularity)—with the density of states of high-temperature superconductors.
They chemically dope graphene to significantly higher levels than previously achieved and then probe its band structure with angle-resolved photoemission spectroscopy. The saddle point becomes more extended than localized as the Fermi surface moves across it. The authors calculate that, under these conditions of doping and Fermi surface topology, graphene can achieve superconductivity, in principle due to electron-electron interactions alone. – Sami Mitra