Networks Evolving on Two Fronts
Road systems, like other networks, change with time while retaining certain features, such as the tendency to have more country roads than eight-lane freeways. To model how networks evolve, researchers tend to focus on the dynamics of either the nodes (cities) or the links (roads). But for a more realistic description, the two aspects should be considered at the same time. Writing in Physical Review Letters, Takaaki Aoki of Kagawa University and Toshio Aoyagi of Kyoto University, both in Japan, have developed a framework that accounts for coevolution in both nodes and links.
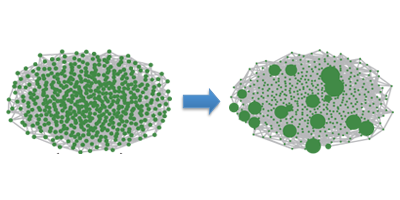
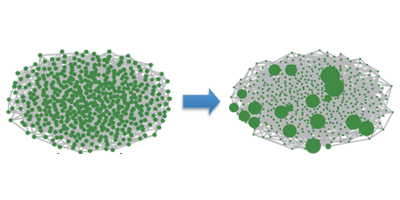
Networks consist of a resource (e.g., people or data) shared among a set of interconnected nodes. Different types of networks exist. In random networks, most nodes have approximately the same number of links. In “scale-free” networks, some “hub” nodes manage more resources than “small” nodes. This more commonly found distribution has a smooth power-law shape, with no peak to indicate a characteristic size, or scale.
In their model, the authors describe each network link by a time-varying weight controlling the rate of traffic. The size of a node can change with time due to diffusion over the weighted links (like people changing cities). In their simulations, the authors started with randomly organized networks and analyzed the relation between weight growth and node size. When links to hub nodes grew sufficiently fast, the networks developed scale-free distributions over time. These distributions were not static, with continuous reshuffling, for example, in the rankings of the top biggest nodes. The authors believe their framework can be applied to a broad range of real-world networks, from prey-predator systems to diffusion-controlled chemical reactions. – Michael Schirber