How Plants Do Their Math
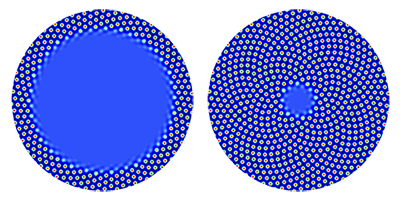
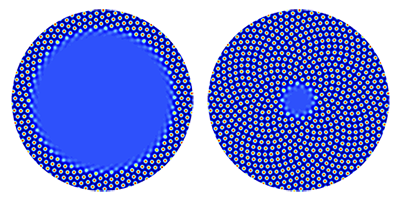
From sunflower seeds to artichoke flowerings, many features in plants follow patterns arranged in terms of Fibonacci numbers: 1, 2, 3, 5, 8, 13… (each number is the sum of the previous two). Research has established that these patterns are optimally packed configurations (of plant organs such as flowers, leaves, or seeds) that maximize access to light and nutrients and thus provide an evolutionary advantage. But how does a plant know how to grow such optimal morphologies? According to a paper in Physical Review Letters, Fibonacci patterns can emerge as a result of the physical and biochemical mechanisms underlying plant growth.
Matthew Pennybacker and Alan C. Newell at the University of Arizona, Tucson, study the case of a sunflower head, in which seeds are grown in annuli surrounding a central region of undifferentiated cells called the meristem—a plant tissue often compared to stem cells in animals. As new seeds are added, the annuli shrink in radius until the head is filled, with the seeds arranged in families of concentric spirals. The authors apply a model that describes how auxin—a growth hormone synthesized by the plant and transported by certain proteins—is distributed within the meristem. The positions in which auxin concentration is maximal indicate where new seeds are formed. Their simulations accurately predict that sunflower seeds form clockwise and counterclockwise spirals, and that the numbers of the two types of spirals are always two consecutive ones in a Fibonacci series. The results suggest that optimal packings may arise in systems described by related families of partial differential equations. – Matteo Rini