Fermi Gas Goes into Deep Degeneracy
A fascinating notion in the study of quantum systems is “universality,” whereby systems of particles having very different microscopic interactions still have the same macroscopic behavior. Reporting in Physical Review Letters, Kiyotaka Aikawa and colleagues at the University of Innsbruck in Austria are the first to cool a gas of identical fermions that exhibit universal dipole scattering—in this case erbium- ( Er) atoms—to a fraction of the Fermi temperature. Their cold-atom system could help physicists better understand the behavior of other dipolar gases, such as cold molecules, and possibly systems in nuclear physics.
The Pauli exclusion principle prevents two identical fermions from occupying the same energy level. As a result, at zero temperature, fermionic atoms like Er will occupy a ladder of quantum states up to the Fermi energy. But the antisymmetric nature of the fermionic wave function prevents identical atoms with short-range interactions from colliding at low temperatures. Without collisions to thermalize the system, evaporative cooling, a standard technique for cooling atomic gases, becomes ineffective.
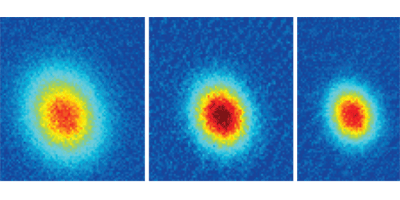
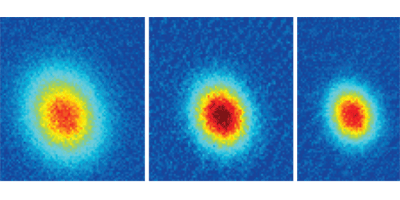
The Innsbruck researchers get around this impasse by using the long-range dipole-dipole interactions of highly magnetic Er atoms to evaporatively cool the gas to 0.2 times the Fermi temperature. The researchers were able to see the onset of the quantum degenerate state by imaging the atoms’ momenta and showing they followed a Fermi-Dirac distribution. The group also demonstrates the universal nature of the scattering cross section in their gas. Specifically, they show the scattering rate between atoms depends only on a single parameter called the dipole length, which is proportional to the product of the atom’s mass and the square of its dipole moment – Kevin Dusling