Ultracold experiments strike universal physics—again
Vitaly Efimov predicted in 1970 [1] that three particles can have an infinity of bound states even when no two of the three are separately bound together. The existence of even a single state so delicate is surprising, but the presence of an infinite sequence of them is doubly so. Even more confounding to our intuition is the fact that making the underlying interactions between the three particles stronger decreases the number of three-body bound states from infinity to a finite value. We normally think, of course, that deepening a potential leads to more bound states, not fewer. Besides a parameter that fixes the short-range behavior of the three bodies, the properties of these Efimov states (as they have come to be called) are universal and characterized by geometric scaling. For instance, given the energy of a bound Efimov three-boson state, you know that the next state is 515 times more weakly bound, and that the state after that is another 515 times more weakly bound, and so on. The spatial size of the states grows by factors of 22.7—the fourth excited state is already at least micron-sized! Geometric scaling is the signature of Efimov states in all low-energy observables.
In the decades since Efimov made his prediction, nuclear, atomic, and molecular physicists have searched for an experimental demonstration. Theoretical suggestions abounded, but no convincing examples were observed until 2006 [2]. Since then, a number of studies have uncovered features identified with Efimov states [3–6]. This veritable flood of experiments is the direct result of technology developed to study ultracold atomic gases—the same technology that led to atomic Bose-Einstein condensates. It was not only the low temperatures, which are essential for observing features related to the very weakly bound Efimov states, but also the ability to control the two-body -wave scattering length that proved critical since Efimov states only appear in the limit of very large scattering length. All of these experiments, however, have measured properties of three-body systems.
Now, Francesca Ferlaino, Rudi Grimm, and colleagues at the Universität Innsbruck in Austria, in collaboration with José Paulo D’Incao from JILA (at the University of Colorado in the US), report [7] on their recent success in experimentally verifying an equally recent prediction [8] for seeing the imprint of Efimov physics on a four-body system. Following up on their success as the first group to measure an Efimov state, the Grimm group has now performed the first quantitative measurement of the ultracold four-body recombination rate. Using ultracold cesium atoms as in their previous experiment, they have not only measured the four-body recombination rate, but also determined its dependence on the cesium-cesium scattering length.
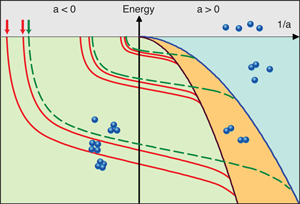
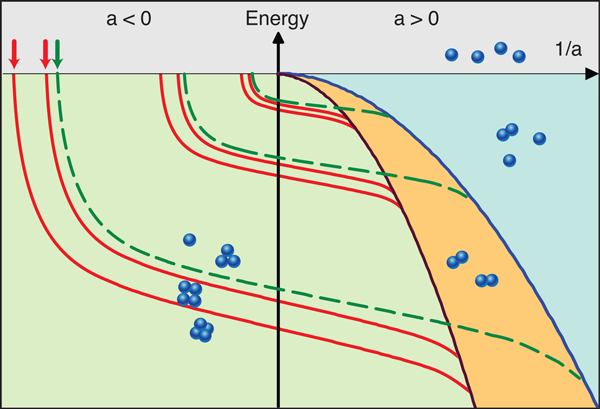
The evolution of the Efimov states for four identical bosons with the scattering length is well-summarized by Fig. 1, which is modeled after one in Efimov’s own work (and Refs. [7,8]). Zero energy corresponds to four free atoms, which is the typical initial state of the system for an ultracold gas. For , there are no two-body bound states, and for there is a weakly bound two-body state with energy . Positive thus finds two lower thresholds for and . The Efimov effect occurs at in the middle of the figure. At that point, there are an infinite number of three-body bound states, labeled to account for all four atoms, where the green lines intersect the energy axis. Note that any given green curve can be obtained from its neighbors via scaling by a factor of 22.7 in the horizontal direction and 515 in the vertical. As is tuned away from infinity, Efimov states are converted to four free atoms for and into for . As suggested in [9] and confirmed in [8], there are also two four-body bound states, , for each Efimov trimer whose energy is universally related to the trimer energy (red lines).
It is these four-body states that the Grimm group found. Since they could not directly observe these states, they did the next best thing and looked for their effect on the low-energy four-body recombination. Four-body recombination is a rich problem with several outcomes,
all of which lead to loss of atoms since the binding energy freed in each process is converted to relative kinetic energy of the products and is typically larger than the depth of the external trapping potential. Monitoring this loss as a function of time yields the rate constant for four-body recombination via the rate equation for the atomic density
(More sophisticated modeling of the density evolution to separate three- and four-body contributions is actually needed and is explained clearly in Ref. [7].) Normally, this loss and the loss from three-body recombination is considered a bad thing that should be avoided. In certain cases, though, like studying few-body physics, the loss provides a window not otherwise available.
Given that the contribution of four-body collisions to the rate equation is proportional to , it is remarkable they can even play a role in the dilute environment of ultracold gases. They do so primarily where they are resonantly enhanced. From the figure, a resonance in occurs for whenever a tetramer line intersects the four-body continuum at zero energy [8]. This tetramer can only be an intermediate resonant state, however, since energy and momentum conservation require at least two fragments finally. The tetramer resonance thus decays into one of the final products above.
Using a breakthrough in nonperturbative calculations for four-body collisions [10], von Stecher, D’Incao, and Greene calculated for four identical bosons for the first time in Ref. [8]. While analyzing their results, they realized that losses due to four-body collisions would appear in the three-body recombination rate measured in 2006 by Grimm’s group since no special effort was taken to separate three-body from four-body losses. This was perfectly reasonable at the time since no one even imagined that four-body collisions would play any role at all. So, von Stecher, D’Incao, and Greene re-examined the three-body recombination rate published by the Grimm group in Ref. [2] and came to the surprising conclusion that one of the four-body resonances had already been observed! This, in turn, motivated Ferlaino et al. to revisit the measurement, taking care to separate three- and four-body processes. The result is the present work showing evidence for both four-body resonant states at approximately the predicted universal positions.
Many open questions about ultracold few-body systems remain. For instance, only single three-body Efimov features have so far been observed experimentally. Verifying the geometric scaling of the features by measuring several in sequence would be very exciting. The ultracold few-body physics of reactive scattering has received little attention, but could prove critical for experiments with cold molecules. In four-body systems, Ferlaino et al. studied only , but point out that the physics for is much richer (see Fig. 1) and should be the subject of future studies. The larger role of the Efimov effect in ultracold heteronuclear four-body processes has just barely begun to be studied in Refs. [11,12], but will almost certainly prove important for the many ultracold experiments that mix different species. The experiment that probably most captures the imagination, though, is producing and trapping these intriguing Efimov trimers for direct study.
In many ways, few-body physics has come full circle in ultracold physics. The physics of Efimov’s effect was introduced in ultracold three-body collisions to help explain their behavior [13]. Since then, it has come to be understood that the fundamental physics behind Efimov’s effect underlies all ultracold three-body collisions whether boson or fermion. In turn, ultracold atomic physics experiments, with their tunability and clean probes, were recognized as the best chance for unambiguously observing Efimov states. These states had been sought in their original context of nuclear physics for years without success since nature does not provide systems with the huge scattering lengths necessary. Rudi Grimm’s group has been leading the experimental charge to study Efimov states, and with their latest work, have shown that even four-body collisions can be important loss processes in ultracold gases.
References
- V. Efimov, Phys. Lett. 33B, 563 (1970)
- T. Kraemer et al., Nature 440, 315 (2006)
- S. Knoop et al., Nature Phys. 5, 227 (2009)
- T. B. Ottenstein et al., Phys. Rev. Lett. 101, 203202 (2008)
- J. H. Huckans et al., arxiv:0810.3288 (2008)
- G. Barontini et al., arxiv:0901.4584 (2009)
- F. Ferlaino, S. Knoop, M. Berninger, W. Harm, J. P. D’Incao, H-C. Nägerl, and R. Grimm, Phys. Rev. Lett. 102, 140401 (2009)
- J. von Stecher, J. P. D'Incao, and C. H. Greene, Nature Phys. (to be published); arxiv:0810.3876 (2008)
- L. Platter, H.-W. Hammer, and Ulf-G. Meissner, Phys. Rev. A 70, 052101 (2004)
- J. von Stecher, Ph.D. thesis, University of Colorado (2008)
- B. Marcelis, S. J. J. M. F. Kokkelmans, G.V. Shlyapnikov, and D.S. Petrov, Phys. Rev. A 77, 032707 (2008)
- Y. Wang and B. D. Esry, Phys. Rev. Lett. 102 133201 (2009)
- B. D. Esry, C. H. Greene, Y. Zhou, and C. D. Lin, J. Phys. B 29, L51 (1996)