Weak measurements just got stronger

Sandu Popescu

Viewpoint

Weak measurements just got stronger

H. H. Wills Physics Laboratory, University of Bristol, Bristol BS8 1TL, UK

April 27, 2009• Physics 2, 32

In the weird world of quantum mechanics, looking at time flowing backwards allows us to look forward to precision measurements.

Figure caption — **Figure 1:** Experimental configuration used by Dixon *et al.* for measurement of femtoradian angular displacements. A laser beam enters a Sagnac interferometer through an optical fiber and the output is monitored for amplitude changes by a CCD camera and for deflections by a quadrant detector. The changes to be measured are produced by motions induced in one of the mirrors by a piezoelectric actuator. Other elements in the optical path are a half-wave plate (HWP), a Soleil-Babinet compensator (SBC), and a polarizing beamsplitter (BS). (Adapted from P. B. Dixon *et al.* [2])

In 1964 when Yakir Aharonov, Peter Bergman, and Joel Lebowitz started to think seriously about the issue of the arrow of time in quantum mechanics [1]—whether time only flows from the past to the future or also from the future to the past—none of them could have possibly imagined that their esoteric quest would one day lead to one of the most powerful amplification methods in physics. But in the weird, unpredictable, yet wonderful way in which physics works, one is a direct, logical, consequence of the other. As reported in Physical Review Letters by P. Ben Dixon, David J. Starling, Andrew N. Jordan, and John C. Howell at the University of Rochester this amplification method makes it possible to measure angles of a few hundred femtoradians and displacements of 20 femtometers, about the size of an atomic nucleus [2].

In classical mechanics if we know the initial conditions of a particle—its initial position and velocity—and the forces that act on it at all times, then we know everything about the particle. No measurement performed in the future can tell us anything new—we can compute its results from what we already know. Similarly, we don’t need to be told anything about the past—we can compute that as well. Quantum mechanically, however, the situation is dramatically different. Suppose we know the initial conditions, the wave function $| Ψ 〉$ at time $t_{0}$ , and know the dynamics (the Hamiltonian) at all times. Still, in general, we cannot predict the result of a measurement performed at a later time $t_{1}$ . We can calculate the probabilities for the different possible outcomes, but not which of them will actually occur. So the measurement at $t_{1}$ yields new information, information that was not available at any other earlier times.

All the above was well known from the early days of quantum mechanics. What Aharonov, Bergman, and Lebowitz realized, however, is that the outcome of the later measurement not only can be used for calculating the behavior of the particle for even later times $t > t_{1}$ , as it was universally considered, but also has implications about the past too. Indeed, suppose we start with an ensemble of particles, each prepared at time $t_{0}$ in the same initial state $| Ψ 〉$ . At some intermediate time $t$ , where $t_{0} < t < t_{1}$ , we subject each particle to some measurement and later, at $t_{1}$ , we perform a final measurement. We can now split the original ensemble into sub-ensembles according to the result of the final measurement. Each of these sub-ensembles is usually called a “pre- and post-selected ensemble.” The statistics of the results of the measurements at the intermediate time $t$ are, in general, different in each pre- and post-selected ensemble, and different from the statistics over the initial, pre-selected-only ensemble. So the results at time $t$ depend not only on what happened at the earlier time $t_{0}$ , but also on what happens at the later time $t_{1}$ .

By pre- and post-selection one can prepare strange sub-ensembles. We could, for example, start with spin 1/2 particles polarized “up” along the $z$ direction and at $t_{1}$ perform a measurement of the spin in the $x$ direction and select only the cases when the spin turned out to be up along $x$ . Then, at any intermediate time $t$ , the spin components in both the $z$ and the $x$ directions (two noncommuting observables) are completely determined—something of a quantum impossibility. But how do we know that both spin components are completely defined? Well, suppose the Hamiltonian is zero (no magnetic field) so that the spin doesn’t precess. If at time $t$ we measure the spin in the $z$ direction we must find it up—it was prepared so at $t_{0}$ . On the other hand, if instead we measure the spin along $x$ , we must also find it up—otherwise the measurement at $t_{1}$ couldn’t find it up.

One may legitimately wonder, however, if this isn’t completely trivial. Indeed, we can play a similar game in classical physics as well, with any system—coins, dice, and so on, where the results are probabilistic. Selecting according to the results of a later experiment can affect the statistics of an earlier experiment, and there is no mystery here—no future affecting the past. The difference, however, is that if we would know everything at the initial time, say, exactly how the coin is thrown, the friction with the air, etc., we could predict everything at the initial moment. In quantum mechanics there is no way to do this—we need to wait until the later time.

Still, could there be a more compelling argument that at intermediate times the spin is indeed up in both the $x$ and $z$ direction? About two decades after the paper by Aharonov and his colleagues, he made a breakthrough. He asked, “What if at time $t$ , I measure the spin along a direction $φ$ in the $x$ - $z$ plane?” Quantum mechanically, $S_{φ} = S_{x} c o s φ + S_{z} s i n φ$ . If it is indeed true that both $S_{x} = + 1 / 2$ and $S_{z} = + 1 / 2$ , it must be that $S_{φ} = (1 / 2) c o s φ + (1 / 2) s i n φ$ . There was a little problem though: this could yield a value larger that $1 / 2$ , for example, $S_{π / 4} = \sqrt{2} / 2$ , an impossible result. Indeed, the spin in any direction can only take the values of $\pm 1 / 2$ ; Aharonov was predicting a value different from all possible eigenvalues and in fact larger that the largest of them. The idea of the future affecting the past in quantum mechanics seemed doomed.

But Aharonov, together with David Albert and Lev Vaidman [3] understood where the problem was. They realized that measuring $S_{π / 4}$ was tantamount to simultaneously measuring the spin along the $x$ and $z$ directions, an impossible task since they would disturb each other. But one could in fact limit the mutual disturbance if one is willing to pay the penalty of allowing the measurements be less precise. They called such measurements “weak” because of the reduced disturbance and these outcomes are called “weak values.” When such measurements are performed, $S_{π / 4}$ does indeed take the impossible value of $\sqrt{2} / 2$ .

Viewed from one angle, this story is all about fundamental philosophical ideas. Does the spin indeed have a value larger than $1 / 2$ or is the result simply an error in the imprecise measuring device used? Does the spin indeed have both the $x$ spin component and the $z$ one well defined? And, above all, does time indeed flow in two directions in quantum mechanics? To be sure, the strange outcome of the measurement of $S_{π / 4}$ in this pre- and post-selected ensemble could indeed be obtained as an error in the measurement, an error in which the pointer of the measuring apparatus moved more than it should have. The explanation can be fully given by standard quantum mechanics, involving regular past-to-future-only flow of time. But the explanation is cumbersome and involves very intricate interference effects in the measuring device. Assuming that time flows in two directions tremendously simplifies the problem. As far as I can tell, Aharonov, Albert, and Vaidman hold the view that one should indeed accept this strange flow of time. I fully agree. Not everybody agrees though, and this is one of the most profound controversies in quantum mechanics.

Viewed from another angle, however, what you see in the above example is an amplification effect: for all the particles in the pre-and post selected ensemble, the pointer of the measuring device moves more than usual. Forget all the philosophy; the amplification still remains. And it doesn’t even need to be quantum—the quantum interference responsible for the movement of the pointer can be mimicked by classical waves. And amplify it does. In a recent paper, Hosten and Kwiat et al. [4] use this technique to amplify the displacement of a laser beam by a factor of 10000, which allowed them to measure displacements of $1 Å$ and to confirm the existence of the Hall effect for light.

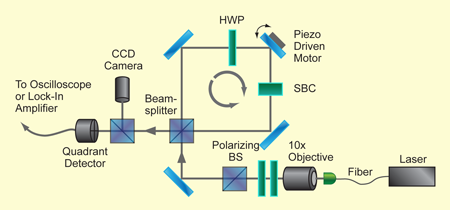
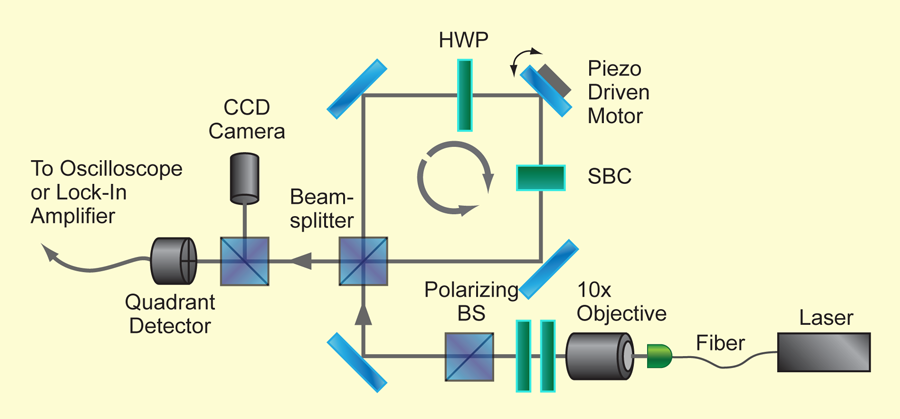
Dixon et al. [2] used a Sagnac interferometer (Fig. 1) with a moving mirror that can be rotated by a piezoelectric crystal. The pre-selection is done by simply sending photons into the interferometer. Once inside, a photon can move clockwise or counterclockwise; this is the quantum variable that is measured. When the mirror is tilted from 45 degrees, the clockwise and counterclockwise moving photons are deflected up or down, respectively, from the central trajectory. The deflection is the “pointer,” which registers which way (clockwise or counterclockwise) the photon went. The post-selection is made by considering only photons emerging towards the detector; this is a post-selection because photons could also exit the interferometer through the other face of the beam splitter. As in the case of the spin $1 / 2$ particle described above, the post-selected beam is deflected more than it would be in the absence of the post-selection.

Examined in detail, this extra deflection results from an interference effect between two overlapping beams, one due to the photons that moved clockwise and one due to the counterclockwise ones. Each of them is moved only a little—up or down—with the expected “normal” shift, but they interfere destructively in most of the regions and only a lower intensity beam survives, moved off center by a much larger amount. The output beam falls on a quadrant detector that registers its displacement.

The experiment looks deceptively simple. It is nothing but. The amplification obtained is only of the order of 100, much smaller than in the experiment of Hosten and Kwiat [4]. But the amplification is added on top of an arrangement that was already very sensitive due to a number of clever tricks (though not all details are given). Conceptually they have also accomplished quite a feat: the mapping of the experiment onto the theory is highly nontrivial. In particular, they used an arrangement in which the “weak value” is a purely imaginary number—yes, that is possible as well. So while the quest for understanding the flow of time continues, high-precision measurements just got better.

References

Y. Aharonov, P. G. Bergmann, and J. Lebowitz, Phys. Rev 134, B1410 (1964)
P. B. Dixon, D. J. Starling, A. N. Jordan, and J. C. Howell, Phys. Rev. Lett. 102, 173601 (2009)
Y. Aharonov, D. Z. Albert, and L. Vaidman, Phys. Rev. Lett. 60, 1351 (1988)
O. Hosten and P. Kwiat, Science 319, 787 (2008)

About the Author

Sandu Popescu is Professor of Physics at the University of Bristol. Between 1996 and 2008 he was also associated with Hewlett-Packard. His research interests center on fundamental aspects of quantum physics, in particular gaining a better understanding of the nature of quantum behavior. A major focus of his research has been quantum nonlocality. This led him to establish some of the central concepts in the area of quantum information and computation. Dr. Popescu has also worked on many other aspects of quantum theory, ranging from the very fundamental, to designing practical experiments (such as the first quantum teleportation experiment) to patentable commercial applications. He was awarded the Adams Prize 2000 for contributions to quantum information.