Melting the world’s smallest raindrop

Marivi Fernández-Serra

Viewpoint

Melting the world’s smallest raindrop

Marivi Fernández-Serra

Physics & Astronomy, State University of New York, Stony Brook, NY 11794-3800, USA

August 10, 2009• Physics 2, 67

Experiments on melting of small water clusters open the door to the study of the size-dependent phase diagram of water.

Figure caption — **Figure 1:** The graph shows the specific heat as a function of $T$ for bulk ice (blue) and small ice clusters (red). The specific heat shows the ratio of the system’s internal energy change to changes in the system’s temperature. In other words, it represents the amount of energy we need to supply to the system to increase its temperature by an infinitesimal amount. This ratio depends on the temperature. As $T$ increases, more vibrational quanta are available to be excited and therefore, for a small increase in temperature, more energy can be stored in the system than at lower $T$ . The melting of ice is a first-order phase transition. There is a discontinuous change in the entropy, associated to the onset of the large configurational entropy of the liquid. This discontinuity is related to a peak that appears in the specific heat curve of the bulk system (blue) as a function of the temperature—this is called the latent heat peak. The melting transition observed for the small water clusters (red) studied by Hock *et al.* happens at a lower temperature. This temperature depends on the size of the cluster (the smaller the size, the lower the melting transition temperature). It also differs from a normal first-order phase transition because the latent heat peak is not observed.

Water is the most ubiquitous substance on the surface of earth. Discoveries related to water typically arouse the interest of both scientists and the general public. Much of this interest stems from water’s unusual properties [1,2], the existence of a density maximum in the liquid phase [1], its negative volume of melting [1], and its increasing diffusivity or molecular mobility under pressure [3] being some of the most well known. The study of the extremely rich phase diagram of water [4] and its anomalous properties [5] is an active field of research, but the number of papers reporting experimental work lags behind those based on computer simulations.

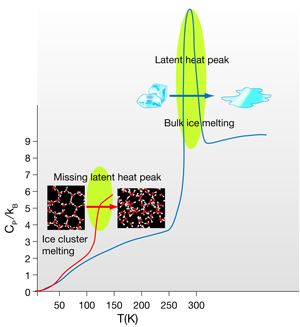
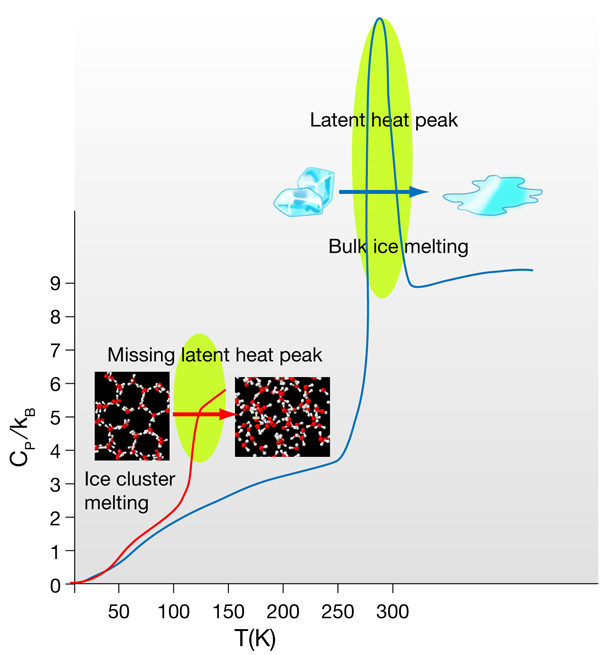
The structure and dynamics of water in any of its condensed forms, and their relation to the aforementioned anomalies, is one of the most prominent open puzzles in science. In a paper published in Physical Review Letters [6], Christian Hock and colleagues at Universität Freiburg in Germany in collaboration with Université Paris Sud in France, study the melting transition of small clusters of water. From the thermodynamic properties of these clusters it is possible to extract information about their structural and bonding characteristics (Fig. 1). This experiment opens a path to the study of the size-dependent phase diagram of water. Such a phase diagram will help us understand many-body effects on the hydrogen bond network of water [2]. It is well known that in water clusters the hydrogen bond strength increases with increasing cluster sizes [2]. The cohesive energy of these clusters cannot be decomposed as the sum of two-body or three-body contributions, an effect known as hydrogen bond cooperativity [2]. The size and temperature dependence of this many-body effect, key to determining the sources of water’s unusual properties, are related to the structure and dynamics of local cluster domains in the liquid phase [4].

The authors use infrared spectroscopy to both heat and characterize size-selected negatively charged clusters of water. The clusters are heated by infrared excitation of the hydrated electron—an additional electron added to an otherwise neutral water cluster. The excited electron decays in less than 200 femtoseconds by coupling to the vibrational modes of the cluster [7]. Using a laser pulse photofragmentation technique [8], the authors perform calorimetric measurements on these clusters. The specific heat of the cluster at a given temperature, $C (T) = δ U (T) / δ T$ , can be calculated from the temperature dependence of the photofragmentation pattern of size-selected anion water clusters. The size of the fragmented pieces is measured using a mass spectrometer. The cluster itself turns out to be a very sensitive calorimeter. One can increase its internal energy before the fragmentation by either controlling the number ( $n$ ) of photons absorbed ( $δ U = n ħ ω$ ) or increasing the cluster temperature in a temperature-controlled external $He$ bath ( $δ T$ ). When the fragments are of the same size, independently of how one heats the cluster, the specific heat is given by the previous formula.

This method allows the researchers to determine the onset of the rapid increase of the specific heat ( $C$ ) as a function of the temperature $T$ . This sudden change in $C$ is associated to the cluster melting transition. The transition $T$ for two well-defined water anionic clusters of size 48 and 118 molecules is presented in their study. The results are not altogether surprising; the onset of the melting temperature ( $T_{m}$ ) decreases as a function of the cluster size.

Previous computer simulation studies had reported similar values, but until now no accurate experiment was available to allow comparisons. The quantum nature of the atomic vibrations at these low temperatures means that the theoretical modeling of the melting of water clusters is very complex and computationally expensive, involving the use of path-integral molecular dynamics [9] with semiempirical interatomic potentials [10] whose accuracy is limited by the model of the water-water interactions itself. Even ab initio potential energies and forces are limited in their description of liquid water [11] and therefore experiments like this have been eagerly anticipated.

Many of the anomalies of water are a manifestation of the fine energy balance between configurational entropy and enthalpy in the underlying network of bonds that keep the molecules together, the hydrogen bond ( $H$ -bond) network. The configurational entropy of water is large; one should think of this as the number of different structural arrangements that the molecules can adopt without paying a large energy cost. The $H$ -bond is relatively weak—more than ten times weaker than the covalent $O$ - $H$ intramolecular bond. It costs little energy to distort the bond, contributing to the large configurational energy of the system. At the same time the strength of the bond is large enough so that the enthalpy of the system is strongly dependent on the average number of bonds broken in the network. At atmospheric pressure the density of liquid water increases on cooling, reaching a maximum of $0.999972 {g/cm}^{3}$ at $277 K$ . At this point the density decreases at a much faster rate and continues decreasing if crystallization is avoided at $273 K$ and a metastable supercooled regime is entered. At atmospheric pressure, water in liquid phase below the freezing temperature is known as supercooled water. It is a metastable state because at that temperature the free energy of the liquid phase is larger than the free energy of the solid, i.e., ice is the ground-state phase. However, the difference is small enough to allow the system to remain in the phase of higher free energy for a small temperature range. The faster the cooling rate, the easier it is to enter the metastability region, where any small perturbation will cause the system to fall to the ground state and crystallize.

The response of the entropy $S$ and density of any system to changes in temperature $T$ and pressure $P$ are represented by the isothermal compressibility (ratio of density change per applied pressure at constant $T$ ) and the isobaric heat capacity (ratio of entropy change per temperature change at constant pressure). In liquid water these two quantities present a minimum within the normal liquid range [2] and show a rapid increase upon cooling and entering the supercooled regime—two more of the many anomalies of water. In bulk systems the melting phase transition is always accompanied by a characteristic peak in the heat capacity as a function of the temperature. The area under this peak corresponds to the latent heat of melting, which in bulk water is of the order of $1.4 kcal/mol$ or $0.05 eV$ per molecule. What happens to the structure of ice when it melts? This energy is mostly used to break about $10 %$ of the $H$ -bonds in ice; while this might not seem to be such a large number, it is enough to make the hexagonal ice (Ih) structure collapse, setting up the diffusion of the molecules that characterizes the liquid state. Water molecules in ice make four $H$ -bonds each, i.e., they are tetracoordinated, forming perfect tetrahedral structures; the 10% of bonds broken at the melting transition only slightly reduce the average coordination to a number in between 3.5 and 4. Water molecules conserve a tetrahedral-like, albeit very distorted, environment. The perfect tetrahedral $H$ -bond network with hexagonal symmetry of ice Ih becomes an amorphous tetrahedral network, with coordination defects that allow the molecules to continuously diffuse around exchanging $H$ -bonds.

In insulating crystals such as ice, the heat capacity reflects the quantum effects of the atomic vibrations. Both Einstein’s and Debye’s specific heat models are derived from the quantum mechanical nature of the phonons in a system. They predict that the heat capacity should decrease with temperature, since vibrational quanta are harder to excite by a small amount of external heat. The high values of the three intramolecular, and two of the three intermolecular vibrational frequencies, only allow a maximum (at $T_{m}$ ) of four degrees of freedom to be active in ice. This is reflected in the value of the specific heat at a given temperature in units of the Boltzmann constant $k_{B}$ . At the temperatures at which Hock et al. carry out their thermal measurements (of the order of $100 K$ ) only two of these vibrations are excited. However, in liquids the specific heat is not only a consequence of the molecular vibrations of the system. In water, in particular, the continuous exchange and distortion of hydrogen bonds within the amorphous $H$ -bonds network has an unusually large contribution to the heat capacity [9], which is of the order of $9 k_{B}$ at room temperature. At the melting point of bulk ice the onset of this liquid configurational entropy is discontinuous, as expected in a first-order phase transition, which translates into the aforementioned sharp peak in the specific heat. However, in Hock et al.’s results this discontinuity is not seen, because, as explained by the authors, phase transitions in small size clusters have a different behavior [12,13].

It is not straightforward to associate the sudden rise of the specific heat at the so-called “melting” temperature to an actual melting transition. Two possible scenarios are compatible with this behavior. As the authors point out, they might just be seeing the onset of the latent heat peak, and the heat capacity might decrease at higher temperatures. The specific heat of small molecular clusters has been theoretically studied and shown to exhibit a broad peak at temperatures well below the bulk $T_{m}$ , which tends to sharpen and shift closer to $T_{m}$ with increasing cluster size [12]. This agrees with the observation that at $T_{m}$ the clusters do not become fully liquid, meaning that the difference in entropy between the solid and “cluster-liquid” state is very small and should decrease with the size of the clusters, making the phase transition continuous. Indeed, the structure of ice clusters as small as the ones studied by the authors is most probably amorphous [14] and not too far from the average structure of the liquid clusters after the transition. A further study with larger clusters at this melting transition should eventually show the appearance of the expected latent heat peak, confirming this scenario.

Looking forward, what is needed is a combination of further experiments like this with theoretical studies of the temperature dependence of the structure and dynamical properties of ice clusters. Even if not mentioned by the authors, understanding the nature of the hydrated electron in water clusters may also help to understand what is happening at the phase transition. An alternative viewpoint, to explain the lack of the latent heat peak and also the temperature dependence of the onset of melting, calls for understanding the spatial localization of the hydrated electron in water clusters. This is another size-dependent question still under debate [15]. The total or partial melting of the clusters may depend on whether the extra electron is located at the surface (a highly possible option for the $H_{2} O_{48}^{-}$ cluster [15]) or inside the cluster. Only pulling together all these elements may solve this small but central area within the larger puzzle of the structure and properties of water.

References

D. Eisenberg and W. Kauzmann, The Structure and Properties of Water (Oxford University Press, Oxford, 1969)[Amazon][WorldCat]
R. Ludwig, Angew. Chem. Int. Ed. 40, 1808 (2001)
C. A. Angell, Ann. Rev. Phys. Chem 55, 559 (2004)
E. Stanley and P. Debenedetti, Physics Today 56, 40 (2003)
P. Kumar, G. Franzese, and H. E. Stanley, Phys. Rev. Lett. 100, 105701 (2008)
C. Hock, M. Schmidt, R. Kuhnen, C. Bartels, L. Ma, H. Haberland, and B. v.Issendorff, Phys. Rev. Lett. 103, 073401 (2009)
A. Bragg, J. Verlet, A. Kammrath, O. Cheshnovsky, and D. Neumark, Science 306, 669 (2004)
M. Schmidt, R. Kusche, W. Kronmüller, B. von Issendorff, and H. Haberland, Phys. Rev. Lett. 79, 99 (1997)
M. Shiga and W. Shinoda, J. Chem. Phys. 123, 134502 (2005)
J. Douady, F. Calvo, and F. Spiegelman, Eur. Phys. J. D 52, 47 (2009)
M. V. Fernández-Serra and E. Artacho, J. Chem. Phys. 121, 11136 (2004)
P. Sheng, R. W. Cohen, and J. R. Schrieffer, J. Phys. C: Solid State Phys. 14, L565 (1981)
D. J. Wales, Energy Landscapes (Cambridge University Press, Cambridge, 2003)[Amazon][WorldCat]
Jan K. Kazimirski and Victoria Buch, J. Phys. Chem. A 107, 9762 (2003)
W. A. Donald, R. D. Leib, J. T. O’Brien, A. I. S. Holm, and E. R. Williams, Proc. Natl. Acad. Sci. 105, 18102 (2008)

About the Author

Marivi Fernández-Serra is a professor in the Physics and Astronomy Department and the Institute for Advanced Computational Sciences at Stony Brook University, New York. Her research focuses on developing and applying electronic structure methods based on density-functional theory. She is interested on understanding properties of water that require a quantum-mechanical description of the underlying atomic interactions. These include the study of the interface between water and light-absorbing materials for energy applications. She received her PhD from the University of Cambridge, UK, in 2005 and has been a Fellow of the American Physical Society since 2020.