Power laws in chess
Finding power laws has now become de rigueur when analyzing popularity distributions. Long tails have been reported for the frequency of word usage in many languages [2], the number of citations of scientific papers [3], the number of visits (hits) to individual websites in a given time interval [4], and many more. In all these cases (including this new one related to chess) the exponent of the distribution is close to . That is, the number of entries (chess openings, words, papers, or websites) with popularity approximately scales as . The semi-universal value of this exponent was first noticed by Zipf [2] when he saw the same statistics apply to such different objects as words ranked by their popularity and cities ranked by their population.
Many scientists proposed simple (and not so simple) models aimed at explaining the origins of this scaling. For city-size distribution, the celebrity list of modelers includes Paul Krugman [5]—the Nobel Prize winning economist and New York Times columnist. Even though the laws of population dynamics responsible for city formation and subsequent growth appear to have very little in common with rules dictating preferences in chess openings, all inverse quadratic power-law distributions became collectively known as “Zipf’s law.” There is indeed something special about the distribution , with = , since it separates the region with a well-defined average ( ) from that where the average formally diverges and thus depends on the upper cutoff ( ). Nevertheless, the quest for the universal “first principles” explanation of Zipf’s law remains elusive.
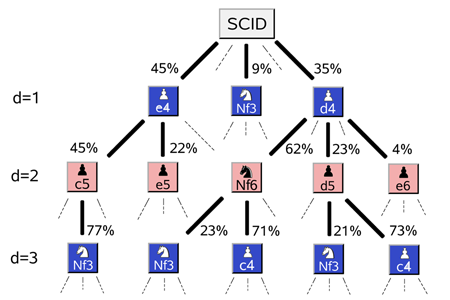
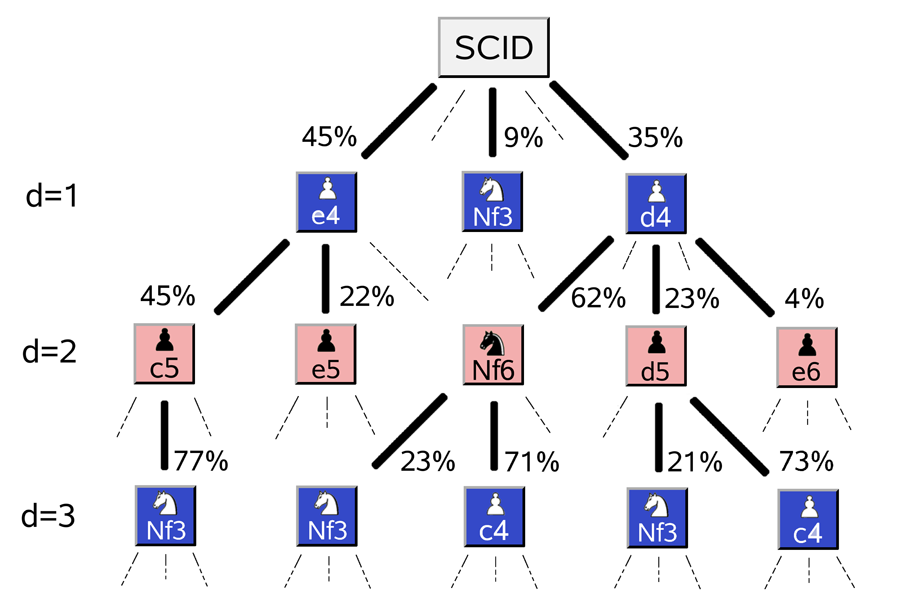
Apart from establishing yet another example of Zipf’s law, the work of Blasius and Tönjes goes a long way towards elucidating its origins in the special case of sequential games or, more generally, any composite multistep decision processes (e.g., complex business or political strategies). These processes are best visualized as decision trees with multiple choices at each level (Fig. 1). The number of possible paths on such trees grows exponentially with the number of steps. As a result, even in the simplest cases the exhaustive enumeration very soon becomes impossible.
The first important observation made by the authors is that if one concentrates on the distribution of popularity of opening sequences limited to the first d steps of the game, it will also be described by a power law, yet with a nonuniversal exponent that linearly grows with the number of moves. The universal Zipf distribution with = is recovered only after these d-dependent distributions are all merged together. The rationale for such a merger leading to double counting is poorly explained in the paper. Nonuniversal power-law exponents often implicate multiplicative random walks [6–8] and this case is no exception. Other examples of power laws generated by multiplicative random walks include wealth of individuals [9], stock prices and their drawdowns (deviations down from the maximum) [10], gene family sizes expanding by gene duplication [11], and many others.
One way to calculate the popularity of a particular opening sequence is to notice that every sequential move of the sequence reduces the number of games in the database that open with these moves by a factor . These factors are the same as branching ratios illustrated in Fig. 1. If the total number of recorded games is (which is million in the professional chess database ScidBase [12] used in this work) then the number of openings starting with a particular sequence of moves is given by ( . The value ( serves as an absorbing lower boundary for this multiplicative process. When a random walker hits such an absorbing boundary it stops moving altogether. In the case of chess opening, once the diversity is down to just one realization, a unique move will be selected at each subsequent time step and ( will remain at until the end of the game. In the case of standard (additive) random walks, a boundary generally gives rise to an exponential Boltzmann distribution. For multiplicative random walks after the logarithmic change of variables [6,7], this exponential distribution becomes a power law.
The exponent of the high-popularity tail of the distribution can be analytically derived for some special cases of the distribution of ratios : (see Eq. (6) in the paper of Blasius and Tönjes [1]). According to these calculations, linearly increases with the number of moves . This is in agreement with the actual distribution of popularity of chess openings. However, the empirically measured , shown in Fig. 3(a) of their paper, has a different profile. Surprisingly, it closely follows the parameter-free distribution . This distribution describes the density of points on a circle projected onto its diameter.
Blasius and Tönjes offer no explanation for this empirical observation. Qualitatively, this profile of makes intuitive sense. At every position of pieces on the chess board, out of many moves allowed by the rules, just one would lead to the most favorable position for the long-term outcome of the game. Such moves that maximize the gradient of “fitness” would be preferentially selected by skillful chess players (the average rating of players in the database puts them between the Candidate Master and the International Master levels). This selection would manifest itself in increasing (and possibly even diverging) as . This divergence is a direct manifestation of players’ skills. Indeed, if I were to play the game of chess against other equally clueless players, the shape of defined by our uninformed random moves would likely to be flatter than that shown in Fig. 3(a) of Ref. [1].
As a suggestion for future studies, it would be interesting to empirically verify this hunch using player ratings included in the ScidBase or other less selective chess databases. In other words, is the distribution of openings selected by the best players significantly different from that selected by the worst players? Another observation made by the authors is that the shape of is independent of the depth of the game . This indicates that, at least at early stages of the game, the phase space of favorable moves does not significantly depend on .
All these empirical facts summarizing the collective knowledge of many chess players have implications for the design of chess-playing computer algorithms. Thinking about chess has a long and venerable history in computer science. One of the founding fathers of information theory, Claude Shannon, has worked on this topic. In his 1950 paper [13] he outlined two possible approaches to designing a computer program playing chess: the brute force strategy, performing the exhaustive evaluation of all possible moves and opponent’s responses for as many steps as computer power would allow. The other strategy is to iteratively select a few of the most promising moves at every step and concentrate computer resources on following a smaller number of more likely paths on the decision tree of the game. The shape of in Ref. [1] provides an empirical justification for this latter strategy that is indeed the one used by modern chess-playing programs.
During the last decade it became customary to blame all types of power laws in popularity on linear preferential attachment mechanisms first used to explain the Zipf’s law by another Nobel Laureate, Herbert Simon [14]. According to these models, the high popularity of certain items is a frozen accident self-sustained by fashion. For example, an initially popular website would acquire new links at a higher rate than its less popular cousins, and as a consequence, further increase its visibility. While in certain situations fashion-driven preferential attachment is likely to be responsible for long tails of popularity distribution, it is reassuring to know that it is not the case in chess—a quintessential game of skill.
References
- B. Blasius and R. Tönjes, Phys. Rev. Lett. 103, 218701 (2009)
- G. K. Zipf, Human Behaviour and the Principle of Least Effort (Addison-Wesley, Cambridge, MA, 1949)[Amazon][WorldCat]
- D. J. de S. Price, Science 149, 510 (1965)
- M. Crovella, M. Taqqu, and A. Bestavros, in A practical guide to heavy tails: statistical techniques and applications, edited by R. J. Adler, R. E. Feldman, and M. S. Taqqu (Birkhäuser, Boston, 1998)[Amazon][WorldCat]
- P. Krugman, J. Japanese Int. Economies 10, 399 (1996)
- M. Levy and S. Solomon, Int. J. Mod. Phys. C 7, 595 (1996)
- D. Sornette and R. Cont, J. Phys. I (France) 7, 431 (1997)
- M. Marsili, S. Maslov, and Y-C. Zhang, Physica 253A, 403 (1998)
- V. Pareto, Cours d'economie politique (F. Rouge, Lausanne, 1896)
- S. Maslov and Y.-C. Zhang, Physica, 262A, 232 (1999)
- M. Huynen and E. Van Nimwegen, Mol. Biol. Evol. 15, 583 (1998)
- http://scid.sourceforge.net
- C. E. Shannon, Philos. Mag. 41, 256 (1950)
- H. A. Simon, Biometrika 42, 425 (1955)