Carbon nanotubes help pairs survive a breakup
Can measurement of one quantum system instantaneously affect the measurement outcome of another, even if the systems are spatially separated? This question has never been clearly answered for solid-state materials. Now, a new experiment by L. G. Herrmann in France, working with colleagues in France, Spain, and Germany, published in Physical Review Letters [1] demonstrates that electrons entangled in a superconducting Cooper pair can be spatially separated into different arms of a carbon nanotube, a material thought favorable for the efficient injection and transport of split, entangled pairs. This work may help pave the way for tests of nonlocal effects in solid-state systems, as well as applications such as quantum teleportation and ultrasecure communication.
The question of nonlocal quantum mechanics plagued physicists for decades, as it seemed to violate the rule of special relativity that information cannot travel faster than the speed of light. In fact, in 1935, Albert Einstein, in collaboration with Boris Podolsky and Nathan Rosen, hoped to disprove nonlocal quantum mechanics by publishing a famous thought experiment describing what is now called “the EPR paradox” [2]. In a simple example of this paradox, two particles, and , are entangled in a spin singlet, = , where and refer to spin up and spin down, respectively. If the singlet is separated into two noninteracting particles, any subsequent measurement of the spin of particle (e.g., found to be up spin) should immediately identify the state of particle (e.g., required to be down spin). Later, John Bell derived a set of inequalities based on correlations between measurements of particles and , and showed that breaking these inequalities would prove quantum nonlocality [3].
The EPR paradox was finally resolved experimentally in the early 1980s, when violations of Bell’s inequalities were verified via polarization-entangled photons [4]; nonlocality has more recently been verified in systems such as ions in optical traps [5] and atom/photon hybrids [6]. However, despite recent advances in the manipulation of entangled electron states [7], Bell’s inequalities have not yet been tested in solid-state systems. Besides the fundamental importance of verifying Bell’s inequalities in materials, spatially separated entangled states could potentially form the basis of advanced technologies such as quantum cryptography, teleportation, or information processing, all of which could be integrated with existing solid-state technology and infrastructure.
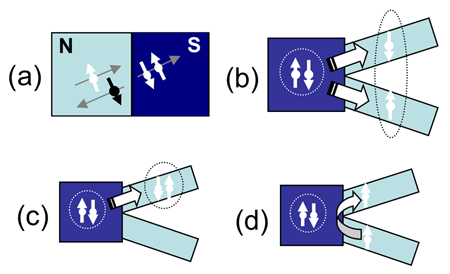
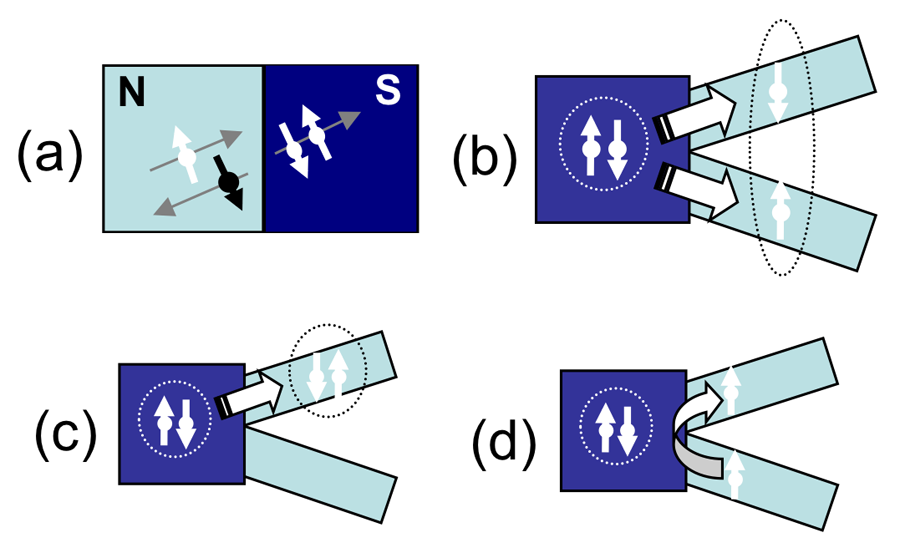
In the experiment by Herrmann et al., the entangled electrons are formed naturally in an -wave superconductor, which consists of spin singlets (Cooper pairs) correlated over the superconducting coherence length. Superconductors have been previously proposed and experimentally verified as an excellent source of EPR pairs [8–11]. Typical charge transfer between a superconductor and a normal metal occurs via a process called “Andreev reflection,” where two electrons in the normal metal pair up to enter the superconductor, and a hole is reflected at the interface to conserve energy (see Fig.1, panel a). In the case of nonlocal transport, also termed “crossed Andreev reflection” (CAR), the incoming electron enters from one normal metal wire, and the hole is reflected in a different, spatially separated wire; this process is equivalent to electrons of a superconducting singlet splitting into two different wires (Fig.1, panel b).
Evidence of CAR was previously demonstrated in groundbreaking experiments that used superconducting pairs injected into two normal metal [11] or ferromagnetic [10] wires. However, these measurements were complicated by the difficulty of distinguishing between contributions from CAR and contributions from pairs tunneling into a single arm (Fig.1, panel c) or from electrons bypassing Andreev reflection and directly tunneling between arms (elastic co-tunneling, see Fig.1, panel d). In addition, CAR signals can be obscured by nonequilibrium effects due to the injection of quasiparticles into the superconductor [12]. A more ideal case in which to test EPR pairs would be if the pair splitting were preferentially enhanced over these other processes. In particular, strong electron interactions—such as Coulomb charging in a quantum dot [8] or correlated states in a one-dimensional wire (e.g., a Luttinger liquid) [9]—could enhance single-particle tunneling over pair tunneling in superconductor-normal injection, thereby enhancing the CAR signal in a split-wire configuration.
Herrmann et al. measure tunneling from a superconductor into two separated quantum dots formed on a carbon nanotube. Quantum dots are isolated puddles of charges where a capacitive charging energy as well as a “particle-in-a-box” quantization energy are required to add additional charges from the leads. Thus simultaneous tunneling of multiple charges into a quantum dot is strongly suppressed. Using this configuration, Hermann et al. observe a strong CAR contribution to the conductance between the superconductor and each of the quantum dots. The conductance is measured at the point of resonance between the dots (where their energy levels line up, so simultaneous tunneling into each dot is enhanced) and then compared to calculations for the superconductor/double-quantum-dot system to extract CAR contributions of up to . In addition, the asymmetry in tunneling between the superconductor and the left or right dot is shown to be consistent with what is expected for a large CAR contribution.
This work is similar to very recent experiments by Hofstetter et al. [13], which also demonstrated enhanced CAR via tunneling from a superconductor into quantum dots; in this case the dots were formed on semiconducting nanowires. However, the experiment on carbon nanotubes not only substantiates the work on nanowires, but also may have significant material advantages. For example, strong electron interactions in the effectively one-dimensional nanotubes are predicted to further enhance pair-splitting processes [9]. Pair splitting is also enhanced by the large quantized energy level spacings in carbon nanotube quantum dots, an effect of their tiny diameters. In addition, metallic carbon nanotubes are predicted to exhibit ballistic transport and long spin-flip scattering lengths, both relevant to the coherent transport of EPR pairs.
The work by Herrmann et al. is important in that it demonstrates that CAR is likely occurring in carbon nanotube quantum dot systems. It sets the stage for future work, in which ideally an experimental parameter can be tuned to separate CAR signals from those of the other tunneling processes. This could be achieved by modifying the gate voltages [13] or various interface transparencies [14], for example. It would also be valuable to clarify the role of the double-dot resonance, as the work on nanowires, in agreement with some theories [8], demonstrated that the relative value of the nonlocal signal was diminished at resonance, likely because the electron number on each dot was not well defined. Finally, a test of Bell’s inequalities requires not just the creation of EPR pairs, but the transport and measurement of them [15]. These measurements entail (1) determining the spin of the electrons in each arm, via spin filters such as polarized ferromagnets, and (2) performing time-resolved spin correlation measurements on currents between the superconductor and each dot. The latter task is quite difficult, due to the large numbers of charge carriers in solid-state systems. A somewhat simpler intermediate step would be to determine noise correlations for transport between the superconducting interface and each quantum dot; correlated signals in this case would be strong evidence of nonlocality [15,16].
Tests of nonlocality in a solid-state system would be a major breakthrough, enabling not only a greater understanding of entanglement in materials, but also the possibility of using separated entangled states for applications. The observation of enhanced nonlocal transport in carbon nanotubes, a material uniquely favorable for the injection and transport of split, entangled charges, offers an exciting new possibility for the study and use of nonlocality.
References
- L. G. Herrmann, F. Portier, P. Roche, A. L. Yeyati, T. Kontos, and C. Strunk, Phys. Rev. Lett. 104, 026801 (2010)
- A. Einstein, B. Podolsky, and N. Rosen, Phys. Rev. 47, 777 (1935)
- J. S. Bell, Physics 1, 195 (1964)
- A. Aspect, P. Grangier, and G. Roger, Phys. Rev. Lett. 49, 91 (1982)
- M. A. Rowe et al., Nature 409 791 (2001)
- D. L. Moehring et al., Phys. Rev. Lett. 93, 090410 (2004)
- J. R. Petta et al., Science 309, 2180 (2005)
- P. Recher, E. V. Sukhorukov, and D. Loss, Phys. Rev. B 63 165314 (2001)
- C. Bena, S. Vishveshwara, L. Balents, and M. P. A. Fisher, Phys.Rev. Lett. 89, 037901 (2002)
- D. Beckmann, H. B. Weber, and H. v. Löhneysen, Phys. Rev. Lett. 93, 197003 (2004)
- S. Russo, M. Kroug, T. M. Klapwijk, and A. F. Morpurgo, Phys. Rev. Lett. 95, 027002 (2005)
- P. Cadden-Zimansky and V. Chandrasekhar, Phys. Rev. Lett. 97, 237003 (2006)
- L. Hofstetter, S. Csonka, J. Nygard, and C. Schonenberger, Nature 461 960 (2009)
- A. Kleine, A. Baumgartner, J. Trbovic, and C. Schonenberger, EPL 87, 27011 (2009)
- V. Bouchiat et al., Nanotechnology 14, 77 (2003)
- G. B. Lesovik, T. Martin, and G. Blatter, Euro. Phys. J. B 24 287 (2001)