A real-time view of elementary excitations in high- superconductors
Understanding high-transition-temperature superconductivity is among the most challenging problems of modern solid-state physics and considering current discussions [1–4], we still have some way to go before the puzzle is solved. Textbooks tell us that in conventional superconductors like lead, an energy gap opens in the electronic density of states around the Fermi level at temperatures below the critical temperature . So-called Cooper pairs, which are bosons consisting of two electrons coupled by a phonon, carry the electrical current without losses. In high- superconductors, the coupling mechanism has been under intense investigation for more than two decades.
Even though this major question is still open, these efforts have led to important developments regarding the quality and analysis of experimental data. In this respect, solid-state research has, in general, profited from this struggle. The major experimental approaches that have contributed to this progress are scanning tunneling spectroscopy, angle-resolved photoemission spectroscopy, and neutron scattering, i.e., methods that work in the momentum-energy domain. Writing in Physical Review Letters, Alexej Pashkin, part of a research team at the University of Konstanz, Germany, and co-workers in Switzerland, China, Israel, and Slovenia show that time-domain spectroscopy can directly access coupling of the elementary excitations that are so essential in understanding high- superconductors [5]. There is a conceptual difference between the above-mentioned energy domain techniques, which measure the spectral function of the particles under study, and time-domain approaches analyzing the response of the system to an external stimulus. As a result, these researchers have been able to investigate the dynamics of formation and relaxation of an excited population of electrons and phonons in a superconductor.
There are challenges in probing the most relevant particles or excitations. Pashkin et al. have now demonstrated what detailed microscopic information on elementary excitations can be obtained in the time domain for a complex material like the high- superconductor (YBCO), once several of these challenges are mastered.
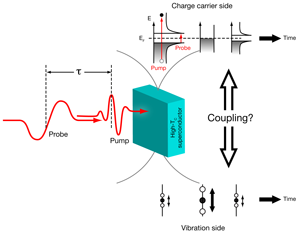
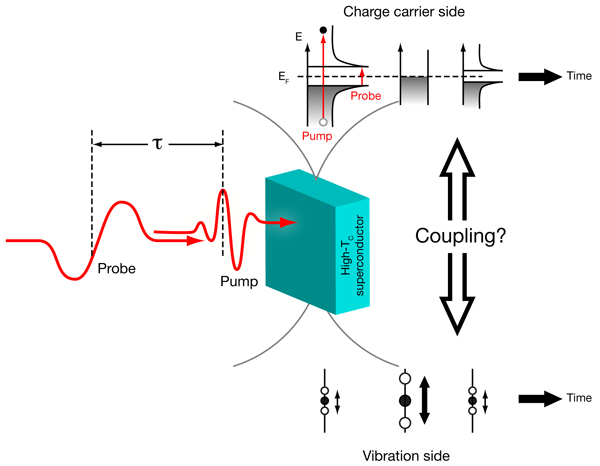
Specifically, the authors had to (i) deal with a superconducting gap below - width and probe the relevant lattice vibrations with specificity, (ii) ensure that the time-resolution was high enough to be sensitive to the changes induced by an optical excitation, which required ultrashort pulse durations, and last but not least, (iii) use suitable high-quality samples for their setup. With these goals in mind, Pashkin et al. employed extremely short femtosecond pulses, which provided, besides central frequency, a bandwidth of several . This enabled them to investigate in reflection geometry a system with pronounced phonon resonances in the THz spectral range. For excitation, they employed the same near-infrared (NIR) laser pulse that also generated the pulse in a nonlinear optical crystal. Hence the employed NIR-pump and -probe pulses were intrinsically synchronized. By modifying the time delay between both pulses they were able to monitor the time-dependent response of the material to the optical excitation by means of the reflectivity to the field (Fig. 1).
Why are these pump and probe pulses the best for this experiment and in what sense are they specific to the elementary excitations in high- superconductors? First of all, the frequency is in the range of the superconducting gap (see Fig. 1, top), and pronounced changes in the reflectivity occur if the system is heated above . In addition, two optical phonon modes show up as sharp resonances in the spectrum (Fig. 1, bottom). Therefore, the technique is sensitive to two sides of the problem: charge carriers and lattice vibrations. Furthermore, the electronic and the phononic part of the response can be nicely separated. If the electric field is polarized along the plane where the superconducting condensate is localized, electronic excitations of the condensate, i.e., charge carriers, are monitored. If the polarization is set perpendicular to that plane, IR active phonons with a vibration amplitude perpendicular to the plane show up as sharp and intense resonances.
In their paper, Pashkin et al. focus on the analysis of the line shape and center frequency of the so-called apex oxygen vibration in YBCO. The core observation of the work is that the center frequency and the asymmetry of the resonance show clearly a different time-dependent behavior, which facilitates conclusions regarding the microscopic nature of electron-phonon coupling. The asymmetry in the phonon resonance is understood to occur due to local screening of the vibration by means of coupling to a collective electronic excitation, which forms exclusively in the superconducting state (the so-called Josephson plasmon). Hence the time-dependent asymmetry bears information on how long it takes until the pump pulse has destroyed the superconducting state and on what time scale the superconducting state reforms after relaxation of the excited state. The second quantity, which is analyzed as a function of pump-probe delay, is the center frequency of the mode. It changes on a similar time scale as the line asymmetry. However, it relaxes much more quickly back to the initial value. Such a shift in the center frequency occurs due to anharmonic effects. The authors can assess the phonon population from this shift because a certain anharmonicity requires a particular population.
By comparing the various time-dependencies of these signatures and without the need of model calculations, Pashkin et al. conclude that the phonon population occurs and relaxes on very similar time scales below and above . The conclusion is that population of phonons actually competes with destruction of the superconducting condensate. In other words, the dynamics of reduction and reforming of the superconducting state, and population buildup and decay of the apex phonons, proceed, by and large, independently of each other. This explains why a simple thermodynamic estimate of the energy density required for driving the superconductor in the normal conducting state is about an order of magnitude smaller than the one that is actually required to achieve this in the pump-probe experiment.
In a more general view, the study shows that a description of the real-time dynamics cannot be achieved by a simple assignment of elementary processes to specific time intervals. In the field, the so-called two-temperature model [6], which links thermodynamic descriptions to the measured time-dependence, is established and widely used. The underlying assumption of this model is that pump energy is initially deposited in the system by electron-hole-pair excitation and that the generated hot carriers scatter with each other and form a thermalized electron distribution function before significant energy transfer into further excitations, like phonons, occurs. Since in the present experiment the superconducting state is destroyed and phonons are populated simultaneously, this model cannot hold in general. It is very likely that such energy transfer dynamics is strongly material dependent and depends on the coupling strength of particular modes.
For , another high superconductor, my co-workers and I were able to measure the electron distribution function directly, using a time- and angle-resolved photoemission experiment [7], and it was found that under similar experimental conditions, more than of the hot charge carriers do form a thermalized Fermi-Dirac distribution function. An obvious question that might be investigated soon is how the experimental approach of Pashkin et al. traces excitations in other high- superconductors, like , as well as other materials of interest, like the recently discovered iron-based superconductors. Therefore, the understanding of the energy transfer dynamics and coupling of excitations in these complex materials will strongly benefit from the specificity to electronic and vibrational excitations that has been established by these researchers.
References
- J. Bouvier and J. Bok, Adv. Condens. Matter Phys. 2010, 472636 (2010)
- T. Dahm, V. Hinkov, S. V. Borisenko, A. A. Kordyuk, V. B. Zabolotnyy, J. Fink, B. Büchner, D. J. Scalapino, W. Hanke, and B. Keimer, Nature Phys. 5, 217 (2009)
- P. W. Anderson, Science 317, 1705 (2007)
- T. Cuk, D. H. Lu, X. J. Zhou, Z.-X. Shen, T. P. Devereaux, and N. Nagaosa, Phys. Status Solidi (b) 242, 11 (2005)
- A. Pashkin, M. Porer, M. Beyer, K. W. Kim, A. Dubroka, C. Bernhard, X. Yao, Y. Dagan, R. Hackl, A. Erb, J. Demsar, R. Huber, and A. Leitenstorfer, Phys. Rev. Lett. 105, 067001 (2010)
- P. B. Allen, Phys. Rev. Lett. 59, 1460 (1987)
- L. Perfetti, P. A. Loukakos, M. Lisowski, U. Bovensiepen, H. Eisaki, and M. Wolf, Phys. Rev. Lett. 99, 197001 (2007)