The carbon challenge
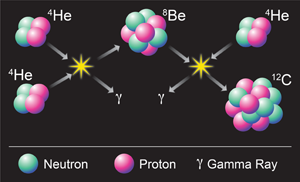
Carbon, so crucial for the chemistry of all living organisms and life in general, forms at the interior of burning stars in what is called the triple-alpha process (Fig. 1): two alpha particles (helium nuclei) react to form beryllium- , which in turn reacts with a third alpha particle to form carbon- . This last step does not produce the carbon- as we know it, however, but rather an excited state called the Hoyle state.
This state is a resonance, meaning it is not localized spatially and it has a finite lifetime governed by its distance (in energy) from the particle-emission threshold. The resonance allows approximately four out of ten thousand decays to produce the ground state of carbon- . Fred Hoyle predicted the resonance in 1954, arguing that without it, stable carbon would not exist [1]. Three years later, an experimental group at Caltech proved he was right [2].
Once carbon is formed, the production of many heavier elements—like the oxygen in our seas and the atmosphere or the silicon needed in cellphones and computers—mostly falls into place. Given its fundamental role, it is natural to ask, Can we understand carbon’s nuclear structure from first principles? And what do we mean by first principles? These are intellectually challenging tasks, which, until recently, have eluded a satisfactory theoretical understanding. Perhaps this is no longer the case. An article appearing in Physical Review Letters by Evgeny Epelbaum of Ruhr University Bochum, Germany, and colleagues [3] aims at a first principles calculation that determines the energies of the ground and Hoyle states of carbon- , as well as other excited states.
Epelbaum et al.’s work deals with a key intellectual issue in ongoing nuclear physics research: understanding the limits of stability of matter starting from basic building blocks (protons and neutrons) and the theory that describes their interaction, ideally starting from quantum chromodynamics. The complex nature of the nuclear forces between protons and neutrons produces diverse nuclear phenomena, characterized by energies of a few kiloelectronvolts to several billions of electronvolts. Capturing this range of energy scales with computations that are tractable poses a tough challenge to nuclear many-body theory and so-called first principles descriptions of nuclear systems. By first principles, we normally mean methods that allow us to solve exactly, or within controlled approximations, either the nonrelativistic Schrödinger equation or the relativistic Dirac equation for many interacting particles. The input to these methods is typically a given Hamiltonian and the relevant degrees of freedom, such as the number of neutrons and protons.
Within this context, Epelbaum et al. are tackling an extremely complicated and tough theoretical problem. Already, the ground state of carbon- is a difficult many-body problem. The Hoyle state lies million electronvolts higher in energy than the ground state, but it has the same total angular momentum ( ) and parity (positive). The fact that the two states share the same quantum numbers, but very different spatial configurations, complicates the calculations. The average density of nuclear matter is much higher than that found in solids or atoms, and the interaction between nucleons is dictated by the strong force. This force, in particular for the important -waves, is repulsive at short distances [less than half of a femtometer ( )] but has an attractive component at intermediate and long ranges (up to – ). For these reasons, models that assume that nuclei are independent particles can’t fully explain what is observed experimentally, for example, the energy levels of the nuclei. Conversely, the consequences of correlations in nuclear many-particle systems are very difficult to measure experimentally and to interpret theoretically. From a theoretical standpoint, a proper understanding of such many-body forces and correlations is crucial in order to provide a predictive many-body theory. Furthermore, it is central to understand which components of the nuclear forces and correlations are responsible for a particular spectroscopic observable. Lastly, a proper many-body theory should quantify the uncertainty in its predictions.
Years of experience in condensed-matter and high-energy physics have shown the power of using lattice Monte Carlo simulations (where physical properties of a system are discretized on a lattice mesh) to predict the properties of many-body systems, see, for example, a recent review in [4]. Building on this knowledge, Epelbaum et al. combine lattice simulations with a Lagrangian derived from effective field theory [5] to predict, numerically, the energy levels and spatial structure of helium- , beryllium- and carbon- . (The Lagrangian is basically a perturbative expansion in powers of the exchanged momentum among nucleons and pions). The group demonstrates how different components of the nuclear forces determine the description of the ground states and excited states of these nuclei. They also provide statistical error estimates and show how many-body forces evolve as more nucleons are added to the nucleus. The parameters in effective field theory for the three-nucleon interaction are fixed to reproduce the binding energy of helium- , while the results for beryllium- , and carbon- are pure predictions. It is important to point out that these calculations would not have been possible without access to modern high-performance computing facilities.
The group’s results agree well with experiment. They also find a resonance for carbon- , which lies close in energy to the experimentally known Hoyle state and its assumed spatial structure, with three alpha particles arranged almost linearly. Their analysis of this state in terms of different contributions to the nuclear interactions is of particular interest. The inclusion of three-nucleon interactions is essential to match experimental results. Ideally, future work will explore the role played by higher-order corrections, such as the inclusion of four-body interactions. However, it is already rewarding for nuclear structure theory that these calculations are able to reproduce, without an a priori assumption about the structure of a given state, the relevant physics of a complicated many-body system.
Other first principles computations have successfully described the structure of several light nuclei [6,7], reactions between light ions [8], and heavier isotopes [9]. Such work holds great promise for a truly quantitative description of nuclei and their properties. Recent and future experimental programs in low-energy nuclear physics aim at exploring the limits of stability of nuclear matter, with wide-ranging consequences for our understanding of nuclear structure and the synthesis of the elements. Correlations beyond an independent particle picture that arise in nuclei towards either the proton or neutron driplines—the predicted limits of the chart of nuclei—should then provide us with a better understanding of shell structures and single-particle properties of nuclei. All of these efforts require models that can extract a simple physical picture from complicated many-body systems. Epelbaum et al. have opened a very interesting path toward the achievements of these ambitious goals.
Acknowledgments
I am much indebted to Thomas Papenbrock for a critical read of the manuscript.
References
- F. Hoyle, Astrophys. J. Suppl. Ser. 1, 121 (1954)
- C. W. Cook et al., Phys. Rev. 107, 508 (1957)
- E. Epelbaum, H. Krebs, D. Lee, and U-G. Meißner, Phys. Rev. Lett. 106, 192501 (2011)
- D. Lee, Prog. Part. Nucl. Phys. 63, 117 (2009)
- E. Epelbaum, H. W. Hammer, and Ulf-G. Meissner, Rev. Mod. Phys. 81, 1773 (2009)
- S. C. Pieper and R. B. Wiringa, Ann. Rev. Nucl. Part. Sci. 51, 53 (2001)
- P. Maris, A. M. Shirokov, and J. P. Vary, Phys. Rev. C 81, 021301 (2010)
- P. Navrátil, S. Quaglioni, I. Stetcu, and B. R. Barrett, J. Phys. G 36, 083101 (2009)
- G. Hagen, T. Papenbrock, D. J. Dean, and M. Hjorth-Jensen, Phys. Rev. Lett. 101, 092502 (2008)