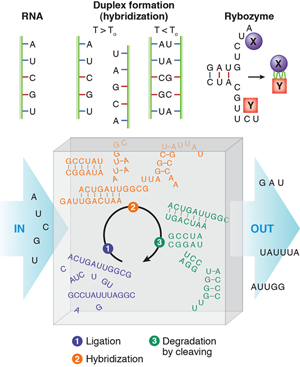
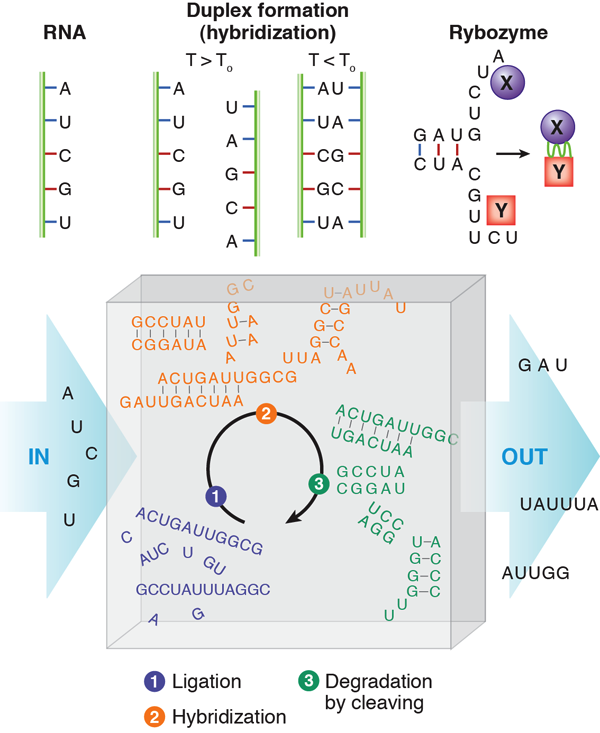
RNA in cycles
In the 1950s, Miller showed that organic biomolecules may spontaneously form [1] from inorganic matter by running electricity through a mixture of gases. Since then, many experiments have shown that molecules that play vital roles in today’s organisms, such as amino acids or the building blocks of DNA and RNA, are likely to have arisen soon after the formation of Earth. However, how a primordial molecular soup of organic building blocks gave rise to self-sustaining reproduction or early forms of life remains unexplained. Writing in Physical Review Letters, Benedikt Obermayer and colleagues at Ludwig Maximilian University of Munich, Germany, report their theoretical efforts to make progress on aspects of this question [2].
The “RNA world” hypothesis [3] proposes that life based on RNA biopolymers predated our current life based on DNA, RNA, and protein. Single-stranded RNA consists of a succession of different bases joined by a backbone. The bases are named adenine (A), guanine (G), cytosine (C) and uracil (U) (see Fig. 1). At moderately elevated temperatures, an RNA molecule may bind to a second strand that is complementary in sequence, in such a way that AU and CG base pairs are formed. This process is called hybridization. Besides carrying the genetic information stored in the succession of bases of an RNA strand through a cell, RNA has other astonishing functions. It can form aptamers, strands that bind very specifically to proteins (just as antibodies can). Special sequences of RNA, called ribozymes, can catalyze other biochemical reactions in a way similar to the action of enzyme proteins. A designed sequence of RNA has been shown to catalyze its own reproduction from other strands [4].
In an RNA world, it is assumed that RNA fulfilled some of the functions that were taken over at a later evolutionary stage by proteins (catalysis) and DNA (information storage). How an accumulation and selection of useful RNA macromolecules on the prebiotic Earth could have occurred has been an object of debate. Accumulation of biological macromolecules may have been driven by temperature gradients, through thermophoresis [5]. Strong temperature gradients exist at the sea floor level, where hydrothermal vents emit many of the suspected building blocks of future biomolecules through porous rocks at high temperatures. In the porous rocks, the temperature gradients produce thermal convection, and molecules transported by the convective flow experience periodic temperature variations.
In their paper [2], Obermayer et al. ask how RNA would behave if it was subject to such periodic conditions in an open reactor. This may be reminiscent of Schuster and Eigen’s famous work on hypercycles [6] considering the evolution, in competition, of multiple, self-reproducing, cyclic, mainly deterministic reactions of RNA and enzymes. In this case, RNA contains the information for the production of enzymes, which in turn multiply the RNA and, at the same time, read the stored information to produce more enzyme. However, Schuster and Eigen introduced molecular self-reproduction by hand from the beginning—unlike Obermayer et al., who consider a real situation: randomly generated RNA folds and hybridizes before it is degraded, and then the process is repeated periodically without self-reproduction. Accordingly, the hypothetical reactor is fed by an influx of the four different RNA building blocks (bases) that will bind (ligate) randomly to produce single-stranded RNA polymers. An imposed condition of length-dependent outflux makes the reaction volume always contain different sequences of various lengths.
In the reactor, the RNA strands produced by ligation will hybridize in a second step (this occurs when a lower temperature of the convection path is reached). Hybridization can lead to two complementary strands forming a double strand, but also to folded single strands that have undergone self-hybridization. Much more complex objects may form when strands of suitable sequences occur by chance.
As a third step, the RNA is degraded (RNA is a rather fragile molecule). Degradation preferentially cuts the RNA at nonhybridized, single-stranded portions, since the base pair formation through hybridization protects bonds from cleavage. Those strands that did not find a complementary sequence in the second step have a good chance of being eliminated in the cleaving process. Once a sequence stabilizes itself by hybridization, or several mutually stabilizing sequences occur, these sequences have a chance to survive during several cycles.
Using extensive computer simulations and theoretical analysis, the authors have studied the situation in great detail. The simulations show an exponential steady-state size distribution of RNA, which becomes wider for lower temperatures. At lower temperature or increased concentration, complex self-hybridizing structures (“hammerhead,” “hairpin,” “double hairpin,” etc.) are more likely to appear. Interestingly, such structures do play important roles in biological organisms. Increased selection pressure in the cleaving step shifts the distributions towards more complex, self-hybridizing sequence motifs. An interesting observation can be made when considering the sequences themselves: Even sequences as short as three base pairs are not randomly distributed. A sequence of six bases may exhibit auto- and cross-correlations over several orders of magnitude in time. Surprisingly, the time correlations of the sequence pool have the same signature as that expected from template-directed reproduction, where molecular scaffolds copy themselves mostly deterministically. The numerical results can be reproduced by a mean-field approach. The average birth and death rate is calculated under the condition that the death rate depends on the likelihood to combine with the complementary partner sequence in order to avoid cleavage. This leads to the same formalism as a template-directed, self-reproducing system, but with a reproduction/death rate below . The system studied by Obermayer et al. is too inefficient to become self-replicating, however, it presents the same type of correlations. Comparison to RNA sequences reveals that some of the smaller selected sequences do indeed play a role in real biological ribozymes. Therefore a pool of potentially useful sequences is selected and maintained by the reactor. This may trigger further evolution of the sequences to higher functions in connection with self-reproduction.
For the most part, molecular recognition protects complementary strands against cleavage, and this leads to greatly enhanced lifetime of certain sequence motifs in the reactor. This, in turn, endows the molecular population with heritable properties through information transmission in an unexpectedly simple process. If, due to a strong fluctuation, the sequence pool has to adapt and changes its composition, this information would be passed on to the following generations. The evolution of the population takes place according to rules, which are set by the population itself.
Neither the periodic cycling, nor the selection process is limited to RNA. Other molecules that mutually protect each other by specific binding could be amplified by an analog selection process. Since the molecules need to bind reversibly in order to be selected, the reactor may well constitute a toolbox for the formation of more complex catalysts, which are the basis of all life forms. In a more general view, the work of Obermayer et al. highlights the fundamental importance of cyclic driving, which has existed throughout the evolution of the earth, and which may well have had a groundbreaking role for the emergence of self-organizing, self-reproductive molecular dynamics that constituted the first forms of life. Concerning the RNA world hypothesis, the paper shows that a suitable molecular toolbox may have occurred spontaneously, in fast and simple ways. This is a strong argument in favor of the theory. Now it remains to be demonstrated that functional ribozymes can form from these elements spontaneously.
References
- Stanley L. Miller, Science 117, 528 (1953)
- B. Obermayer, H. Krammer, D. Braun, and U. Gerland, Phys. Rev. Lett. 107, 018101 (2011)
- Carl R. Woese, The Genetic Code (Harper & Row, New York, 1968)
- W. K. Johnston, P. J. Unrau, M. S. Lawerence, M. E. Glasner, and D. P. Bartel, Science 292, 1325 (2001)
- Philipp Baaske, Franz M. Weinert, Stefan Duhr, Kono H. Lemke, Michael J. Russell, and Dieter Braun, Proc. Nat. Acad. Sci. U.S.A. 104, 9346 (2007)
- M. Eigen and P. Schuster, Naturwissenschaften 64, 541 (1977)