A Closer Connection Between Entanglement and Nonlocality
Entanglement, first introduced by Einstein, Podolsky, and Rosen [1], and Schrödinger [2] in 1935, can arise when two quantum systems are produced from a common source, for instance, when two particles are produced with opposite spin in a decay process. Mathematically, this means that the state of the quantum system cannot be written as a mixture of product states of its constituent subsystems. As shown in 1964 [3], such states can violate a set of relations now called Bell inequalities, implying that quantum theory exhibits a form of nonlocality. That is, entangled quantum systems behave as if they can affect each other instantaneously, even when they are extremely remote from each other. Entanglement and nonlocality are two of the main concepts studied in the quantum information sciences. Although it is immediately clear that entanglement is necessary for nonlocality, a detailed quantitative relation between these two concepts is not yet established. Writing in Physical Review Letters, Francesco Buscemi of the University of Nagoya, Japan, makes important progress in this direction [4].
Nowadays, entanglement is viewed as central to most of quantum information science. It is at the basis of quantum teleportation and the power of quantum computers, and it is understood to be behind all the really complex quantum phenomena, such as the complex quantum phases of matter encountered in solid-state physics. Entanglement thus represents a genuinely quantum resource. In particular, two initially independent parties necessarily need to exchange quantum systems to establish a shared entangled state: the exchange of classical messages is not sufficient to create, or even increase, entanglement. This observation is at the basis of the quantitative study of entanglement, which classifies and measures the entanglement content of quantum states by considering how they can, or cannot, be interconverted using what is known as “local operations and classical communication” (LOCC).
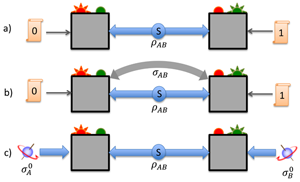
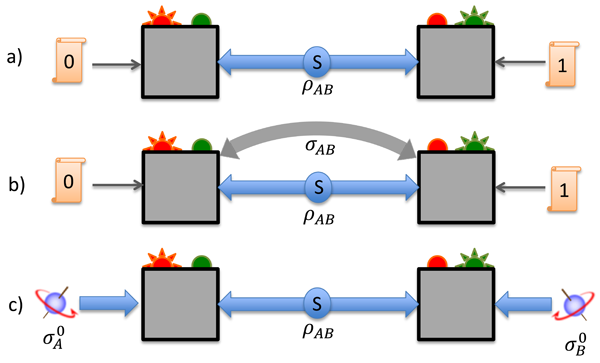
Although entanglement is a purely quantum phenomenon, its consequences in the laboratory are ultimately formulated in terms of classical quantities. Indeed, a measurement apparatus can be seen as a device that receives classical instructions (what measurement to perform) and produces classical results (the measurement outcome). Even if prior quantum messages are necessary to generate entanglement between initially independent parties, couldn’t the exchange of prior classical messages be sufficient to reproduce these classical measurement statistics? For generic entangled states (actually, for all pure entangled states [5]), the answer is no! Indeed, the correlations between distant parties that can be generated through the prior exchange of classical messages—what computer scientists call shared randomness—necessarily satisfy Bell inequalities, but the correlations obtained by measuring entangled states violate these inequalities! Such correlations are called nonlocal. Operationally, nonlocality is therefore important because it allows discriminating classical from entangled states simply by analyzing their measurement statistics [see Fig. 1(a)].
The relation between entanglement and nonlocality, however, is more subtle than it appears at first sight and the two concepts are not entirely equivalent. Indeed, there exist mixed entangled states that cannot generate nonlocal correlations, i.e., cannot violate any Bell inequalities [6,7]. Recently, however, Masanes, Liang, and Doherty showed that for any entangled state , there exists another state that does not violate the CHSH inequality (the simplest Bell inequality), but such that the combination of both states is nonlocal [8] (see also Ref. [9]). Thus entangled states always have some hidden nonlocality that can be activated. Figure 1(b) illustrates this scenario. The approach of Masanes, Liang, and Doherty is not entirely satisfactory because, in essence, it provides the measuring devices with access to auxiliary entanglement (the state ). It is not clear, for instance, how to interpret this extra resource in the context of possible applications such as communication complexity or cryptography (more on this below).
In his paper, Buscemi introduces a semiquantum generalization of the usual Bell scenario that makes much tighter the relation between nonlocality and entanglement [4]. Instead of providing the measurement devices with classical instructions, as in the usual Bell scenario, Buscemi considers a situation in which these instructions are written on quantum systems [see Fig. 1(c)]. If distinct instructions correspond to distinguishable quantum states, then the situation is no different than before. But things become more interesting when the measurement instructions correspond to nonorthogonal states that cannot be perfectly distinguished.
A semiquantum Bell scenario is specified by the set of states that are used as inputs for one measuring device and the set of states which are used as inputs for the other measuring device. By analogy with the usual Bell scenario, the correlations between which states are used as inputs and the measurement outputs are called local if they can be reproduced using only shared randomness, and nonlocal if they require entanglement. As in the usual scenario, the local correlations are separated from the nonlocal ones by Bell-type inequalities. The key result of Buscemi [4] is the proof that for each entangled state there exists a semiquantum Bell scenario that reveals through the violation of a Bell-type inequality the entanglement of the state. In particular, the negative result of Refs. [6,7], which showed that some entangled states did not violate any Bell inequality, does not hold in semiquantum Bell scenarios.
To prove this general result, Buscemi uses quantum teleportation—the ability to use prior entanglement to transmit quantum states without sending them physically—in order to spread the information about the inputs between the measuring devices. He also makes contact with quantum state tomography (the procedures used to experimentally characterize quantum states) and entanglement witnesses (operators that can reveal the entanglement of states). Indeed the semiquantum Bell scenarios he considers can be viewed as novel forms of entanglement witnesses. Simultaneously, Buscemi introduces a new class of transformations between entangled states, namely those allowed by local operations and shared randomness, that departs from the usual LOCC paradigm of entanglement theory, but which promises to be a rich avenue of research. These connections are novel. They suggest a possible unification between aspects of quantum information research that previously seemed disconnected.
The work of Buscemi will also have an impact on other areas of quantum information. Communication complexity is a fruitful subfield of computer science that studies the minimal amount of communication required for distributed parties to achieve a given task. Nonlocality and communication complexity are intimately related [10]. The new result [4] suggests that by enlarging the communication complexity scenarios to the case where the inputs are quantum, we will obtain an interesting new class of problems. Finally, entanglement and nonlocality also have deep connections with quantum cryptography [11,12]. This suggests that the new result [4] will lead to an improved understanding of quantum cryptography, as well as other quantum information processing tasks.
References
- A. Einstein, B. Podolsky, and N. Rosen, Phys. Rev. 47, 777 (1935)
- E. Schrödinger, Proc. Cambridge Philos. Soc. 31, 555 (1935); 32, 446 (1936)
- J. S. Bell, Physics 1, 195 (1964)
- F. Buscemi, Phys. Rev. Lett. 108, 200401 (2012)
- N. Gisin, Phys. Lett. A 154, 201 (1991)
- J. Barrett, Phys. Rev. A 65, 042302 (2002)
- R. F. Werner, Phys. Rev. A 40, 4277 (1989)
- L. Masanes, Y.-C. Liang, and A. C. Doherty, Phys. Rev. Lett. 100, 090403 (2008)
- M. Navascues and T. Vertesi, Phys. Rev. Lett. 106, 060403 (2011)
- H. Buhrman, R. Cleve, S. Massar, and R. de Wolf, Rev. Mod. Phys. 82, 665 (2010)
- A. Ekert, Phys. Rev. Lett. 67, 661 (1991)
- A. Acin et al., Phys. Rev. Lett. 98, 230501 (2007)