Trend

High-temperature superconductivity in the iron pnictides

    Michael R. Norman
    • Materials Science Division of Argonne National Laboratory, Argonne, IL 60439
• Physics 1, 21
A new class of high-temperature superconductors has been discovered in layered iron arsenic compounds. Results in this rapidly moving field may shed light on the still unsolved problem of high-temperature cuprate superconductivity.

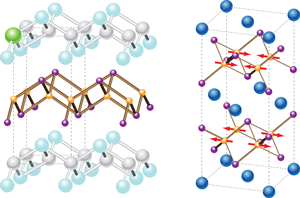
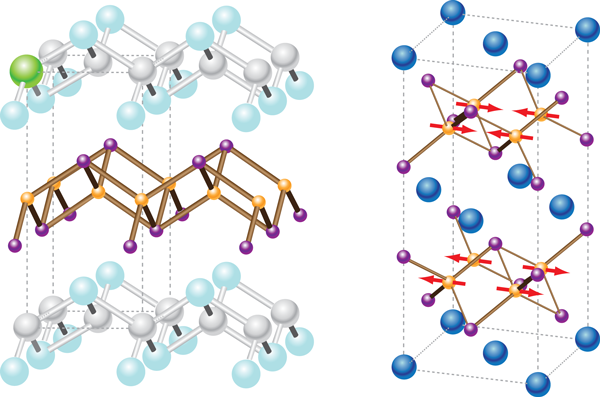
In January of this year, a preprint appeared from the group of Hideo Hosono in Japan showing the existence of superconductivity in a layered iron arsenide material with a transition temperature ( Tc) of 26 K [1]. The paper grew out of an earlier study that found a Tc of 5 K in the phosphide analogue [2]. In some ways the story looked very similar to what had been found 22 years earlier in the cuprates. The parent compound, LaOFeAs, was not superconducting, but upon replacing some of the oxygen by fluorine, the material became superconducting. Even the crystal structure was reminiscent of the cuprates, with layers of FeAs separated by spacer layers of LaO where the fluorine dopants were introduced (Fig. 1, left).

Figure 1: (Left) Crystal structure of the 1111 FeAs material (after [47]). Fluorine (green) replaces oxygen (gray), donating electrons to the FeAs layers. Other atoms shown are iron (yellow), arsenic (purple), and lanthanum (light blue). (Right) Crystal structure of the 122 FeAs material (after [14]). The parent compound of both materials has iron moments (red arrows) that form a striped antiferromagnetic pattern. Calcium atoms are shown in blue.

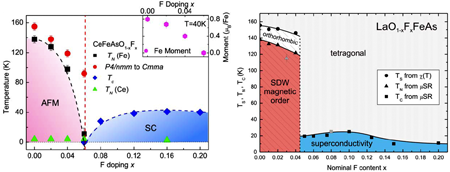
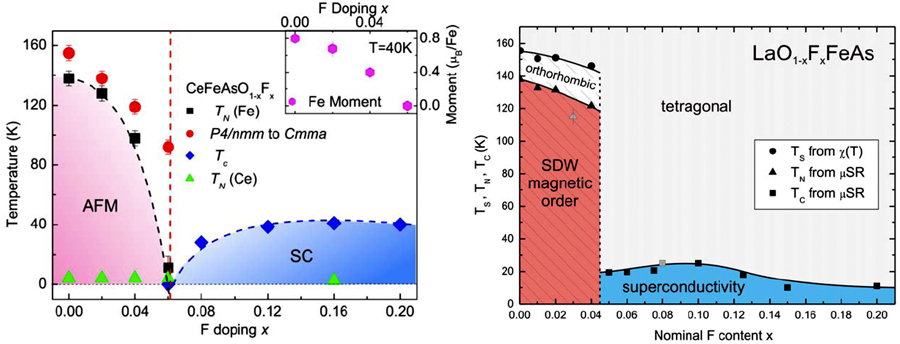
Following these initial observations, subsequent data seemed to strengthen the connection between the cuprates and these so-called “pnictides” (i.e., compounds of the nitrogen group). In particular, the discovery that the spins on the iron atoms in the parent compound order antiferromagnetically seemed to confirm this picture [3]. As in the cuprates and other unconventional superconductors, the material is an antiferromagnet at low doping and increased doping destroys the antiferromagnetism (Fig. 2), leading to superconductivity. As a result, many researchers speculated that the mechanism of superconductivity would be related to that of the cuprates.

Figure 2: (Left) Phase diagram of fluorine doped CeO1−xFxFeAs as determined by neutron scattering (from [16]), showing a smooth (second-order) change from antiferromagnetism (AFM) at low doping to superconductivity (SC) at larger dopings. TN is the magnetic transition, with the inset the value of the staggered magnetic moment. (Right) Phase diagram of fluorine doped LaO1−xFxFeAs (from [17]), showing a more abrupt (first-order) change from spin-density-wave (SDW) antiferromagnetism to superconductivity as a function of fluorine content. Ts is the structural transition.

But, as further work has shown, the story is not so simple and there are important differences between the FeAs materials and cuprates. Although the parent compound in the cuprates is indeed an antiferromagnet, it is a special type—a Mott insulator—where band theory says the material should conduct but the charge carriers are localized because of the large Coulomb repulsion, U, between the electrons. This is in contrast to LaOFeAs, which is an antiferromagnetic “spin-density-wave” metal (with the spins periodically modulated in space) where the electrons appear to be more delocalized. While antiferromagnetic order in a Mott insulator arises because the spins can lower their energy if they are antiparallel to their neighbors, a spin-density wave is typically a collective effect that emerges from an instability of the paramagnetic Fermi surface.

Band calculations based on the local-density approximation (LDA, which is the standard methodology for band theory and the benchmark method against which more sophisticated calculations are measured) to density-functional theory emphasize this difference between these types of antiferromagnetism. For example, band theory predicts that the undoped cuprates are metallic, in contradiction to experiment, implying that LDA underestimates the correlations between the electrons [4]. In contrast, for the FeAs materials, the antiferromagnetism is predicted to be stronger than what is actually observed, meaning LDA may overestimate the correlations [5]. Furthermore, although earlier dynamical mean-field studies (that include local time-dependent correlations between the electrons) assumed an appreciable Coulomb repulsion, U, between the electrons in the FeAs materials [6] comparable to that of the cuprates, recent calculations indicate that the effective U may be small [7].

The reason for the possible smallness of U, which controls the local correlations, is related to another major difference between the cuprates and the FeAs materials. The cuprates are very two dimensional in nature, and the low-energy electrons reside in a single band of carriers formed by the hybridization of the Cu 3d x2-y2 orbitals with oxygen 2p electrons. The net result is that the effective U is only slightly smaller than that expected for localized Cu d electrons. In contrast, all five Fe 3d orbitals contribute to the electronic structure in the vicinity of the Fermi level in the FeAs materials. This orbital mixing, coupled to the appreciable hybridization of the Fe d electrons with the As p electrons, may strongly reduce the effective U as compared to the cuprates.

Moreover, the coppers also sit at symmetry sites that exhibit strong planar coordination, as opposed to the tetrahedral coordination of iron atoms in the FeAs materials. In fact, recent studies indicate that the upper critical magnetic field that destroys superconductivity is only moderately anisotropic in the FeAs materials and the anisotropy actually becomes smaller with increasing magnetic field [8]. This may be good news, actually, since one of the issues that has limited practical applications of cuprates is their extreme anisotropy.

Since the discovery of superconductivity in LaOFeAs—known as the “1111” structure from its formula unit—scientists have made a number of analogues, primarily by substituting other rare earth ions for La (Fig. 1, left). With either doping or pressure, it has been possible to achieve a Tc beyond 50 K [9]. Moreover, a simpler class of materials based on the BaFe2As2 parent compound (the “122” structure, Fig. 1, right) that does not have the LaO spacer layers also superconducts with a comparable Tc to the 1111 materials [10]. More recently, superconductivity at 18 K has been discovered in an even simpler FeSe material [11]. The race is therefore on, just as for the cuprates, to discover materials with increasingly higher Tc. If a material could be discovered with a Tc above the temperature of 77 K where air liquifies (as occurred in the cuprates), then things would become really interesting.

Although the situation changes daily, several important facts have emerged about the physics of these new FeAs materials. The antiferromagnetism of the parent (undoped) compound is somewhat different from that found in the cuprates. It is composed of aligned iron spins that alternate in direction from one row of iron atoms to the next (Fig. 1, right), leading to a stripe-like structure (as opposed to the checkerboard pattern of up and down spins seen in the cuprates) [3,12]. The magnetic phase appears to be associated with a distortion of the crystal lattice from a tetragonal to an orthorhombic structure [12,13]. In some materials, the magnetism seems to be directly tied to the structural transition and in one example it was shown that the magnetic transition follows the hysteresis in temperature associated with the first-order structural transition [14]. In other cases, though, the magnetism appears at a lower temperature than the structural transition, and sometimes does not occur at all. For instance, in NdOFeAs, the iron spins only order when the neodynium spins order, which occurs at a very low temperature [15].

So, what happens when one moves off of stoichiometry by doping? The structural transition is rapidly suppressed, the magnetism collapses, and the material becomes superconducting (Fig. 2 shows the phase diagram associated with this behavior). In some compounds, the magnetism appears to smoothly vanish before superconductivity smoothly turns on (Fig. 2, left) [16]; in other cases, it appears that the magnetism abruptly disappears with the superconductivity abruptly appearing (Fig. 2, right) [17].

The difference between this “second-order” and “first-order” behavior may be a materials issue (as plagued the cuprates in the early days), or simply subtle structural differences between the various compounds. Similar behavior can be achieved by pressure rather than by chemical doping [18]. The primary effect appears to be a “shrinking” of the lattice, leading to greater itineracy of the electrons and the resultant onset of superconductivity. This is particularly clear in the 122 materials, where one sees that superconductivity emerges from a “collapsed” tetragonal phase that differs from both the high-temperature tetragonal and low-temperature orthorhombic phases of the parent compound [19].

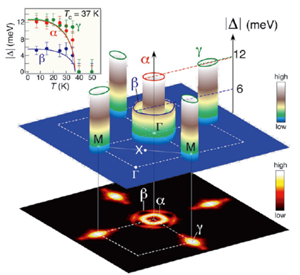
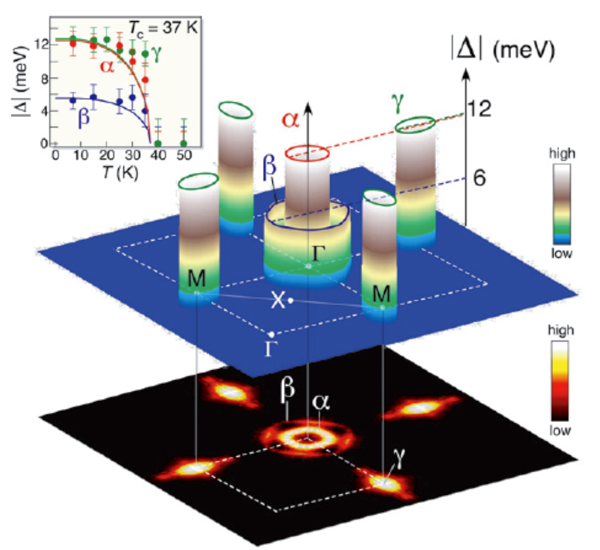
Much of this behavior can be understood from band-structure calculations within the local-density approximation. Although such calculations have a tendency to overestimate the size of the magnetic moment in the parent compound as mentioned above [20], they do find that the stable ground state has the striped magnetic structure observed experimentally, and that this structure is stabilized by the orthorhombic deformation [21]. In addition, the “collapsed” phase is predicted to be nonmagnetic as well [22]. In all phases, band theory predicts a metal with several (mostly cylindrical) Fermi surfaces [23] that are separated by a wave vector that is consistent with the period of the magnetic phase (Fig. 3), leading to a “nesting” picture for the origin of the magnetism, as occurs in chromium. The result is that part of the Fermi surface is destroyed in the magnetic phase [24]. The predicted Fermi surface has been directly observed by angle-resolved photoemission spectroscopy [25], and is consistent as well with a recent quantum oscillation study [26]. Both measurements find relatively modest electronic masses, consistent with itinerant (delocalized) behavior of the electrons.

Figure 3: The Fermi surface and superconducting gap (Δ) of Ba0.6K0.4Fe2As2 as determined from angle-resolved photoemission spectroscopy (from Ding et al. [27]). The Fermi surface is the surface of constant energy in momentum space that separates the filled from the unfilled states. The 3D plot shows the gap at 15 K as a function of the x and y components of the momentum (Γ, M, and X label high symmetry points of the two-dimensional Brillouin zone), with the colors indicating the gap magnitude (the gap amplitude vs temperature is shown in the inset). The gap anisotropy in momentum space is weak, though the gap magnitude differs between the various Fermi surfaces (α, β, γ). The image at the bottom is the photoemission intensity near the Fermi energy.

Angle-resolved photoemission studies have in turn been able to map out the anisotropy in momentum of the superconducting energy gap [27], which is important in identifying the nature of the order parameter associated with the superconducting condensate. Although the magnitude of the gap appears to differ in size from one Fermi surface cylinder to the next, the gap anisotropy on each cylinder is relatively weak. In particular, no evidence for nodes—that is, points in momentum where the energy gap vanishes—has been found. This is supported by other measurements, most notably electron tunneling [28]. In addition, a recent study of the penetration depth of a magnetic field into the superconductor has found an exponential temperature dependence consistent with a nodeless gap [29]. On the other hand, NMR studies [30] have found the ubiquitous T3 behavior of the spin-lattice relaxation rate associated with a gap that has nodes, as seen in cuprates and heavy fermion superconductors. Although this could be a consequence of disorder [31], one should caution that for a number of years, it was thought that cuprates also had a nodeless gap, until detailed measurements on well-characterized samples indicated otherwise, with the location of these nodes consistent with the d-wave symmetry of the order parameter.

Based on the measurements suggesting a relatively isotropic gap, one might jump to the conclusion that these materials are more like classic superconductors such as niobium and lead than the cuprates. But a growing body of theoretical and experimental work suggests otherwise. Theoretical calculations indicate that the electron-phonon coupling is weak [32]. These same calculations predict a phonon spectrum in good agreement with that obtained from inelastic neutron scattering [33]. This would argue against an electron-phonon origin to the superconductivity, though Yildirim has cautioned that given the strong sensitivity of the magnetism to the crystal structure, there may be a strong spin-lattice coupling that could indirectly contribute to superconductivity [22].

In fact, one of the leading candidates to emerge for the superconducting order parameter is the so-called s± state [34]. The nature of this state can be appreciated from Fig. 3. The idea is that the superconducting order parameter has one sign on the cylinders around the Γ point of the Brillouin zone, but the opposite sign on those around the M point (the energy gap being proportional to the modulus of the order parameter). Such a state can be realized in a model where the pairing is mediated by antiferromagnetic spin fluctuations. In this picture, an attractive interaction can be realized if the order parameter changes its sign under translation by the wave vector, q, of the magnetic state (in real space, this gives rise to an oscillatory potential that is attractive for certain spacings of the electrons comprising the Cooper pair). This is exactly the right vector needed to connect the cylinders at Γ to those at M. So, although the order parameter is unconventional, the energy gap has no nodes. The origin of this s± state from microscopic considerations, and its consequences in regards to experimental data, have been treated in a number of other studies [31,35]. Although measurements sensitive to the phase of the condensate have so far not indicated any evidence for sign changes in the order parameter [36], a recent inelastic neutron scattering study has found a spin-one magnetic resonance [37] thought to be associated with a sign change of the superconducting order parameter under translation by q (as observed previously in cuprates and several heavy fermion superconductors).

Of course, these are early days, and many other possibilities exist besides s± pairing induced by antiferromagnetic spin fluctuations. A large variety of other superconducting order parameters associated with differing pairing mechanisms have been proposed, including p-wave [38] and various d-wave and mixed symmetry [39] states. Some of these order parameters have nodes, others do not. Moreover, a variety of microscopic models, most of them based on magnetic fluctuations, have been proposed. The models typically differ in the number of bands thought necessary to capture the low-energy physics—anywhere from two-band models [40] to five-band ones [41]. This is in contrast to cuprates, where a single band of carriers (per CuO2 plane) captures the low-energy physics [42]. So, although the FeAs problem may be simpler than the cuprate one because the electron correlations are weaker, the number of possibilities to describe the superconducting order parameter is much greater because of the multiband nature of the materials. Again, it will take careful measurements on well-characterized samples to definitively address this question. In particular, as in the cuprates, it may ultimately take phase sensitive measurements to finally resolve this issue.

Even if we know the order parameter, this will not “solve” the problem. Phase-sensitive measurements in the cuprates finally nailed down their d-wave symmetry back in the mid 1990s, yet the microscopic theory of these materials is still not determined. Sorting out the multiband nature of the FeAs materials, and the complex role that the magnetism and the crystal structure play, will be necessary before this can be accomplished. And although much has been made recently of the differences these materials have from the cuprates, other studies show some similarities. Various photoemission [43], tunneling [44], and optics [45] studies are quite reminiscent of the cuprates, including the possible presence of a precursor gap (a “pseudogap”) existing above Tc. Pursuing the various similarities and differences between these two classes of materials may help unravel the physics of both of them. If anything, the experience with the cuprates, where different classes of materials have quite different transition temperatures [46], may help point the way to finding variants of the FeAs materials with higher Tc. One can only imagine the impact this could have on technology if an isotropic-like material superconducting above liquid air temperature is found. Then, the true superconductivity revolution that was predicted in 1987 for the cuprates could ultimately be realized in their FeAs cousins.

References

  1. Y. Kamihara, T. Watanabe, M. Hirano, and H. Hosono, J. Am. Chem. Soc. 130, 3296 (2008)
  2. Y. Kamihara, H. Hiramatsu, M. Hirano, R. Kawamura, H. Yanagi, T. Kamiya, and H. Hosono, J. Am. Chem. Soc. 128, 10012 (2006)
  3. C. de la Cruz, Q. Huang, J. W. Lynn, J. Li, W. Ratcliff II, J. L. Zarestky, H. A. Mook, G. F. Chen, J. L. Luo, N. L. Wang, and P. Dai, Nature 453, 899 (2008)
  4. W. E. Pickett, Rev. Mod. Phys. 61, 433 (1989)
  5. I. I. Mazin, M. D. Johannes, L. Boeri, K. Koepernik, and D. J. Singh, Phys. Rev. B 78, 085104 (2008)
  6. K. Haule, J. H. Shim, and G. Kotliar, Phys. Rev. Lett. 100, 226402 (2008)
  7. V. I. Anisimov, D. M. Korotin, S. V. Streltsov, A. V. Kozhevnikov, J. Kunes, A. O. Shorikov, and M. A. Korotin, arXiv:0807.0547
  8. H. Q. Yuan, J. Singleton, F. F. Balakirev, G. F. Chen, J. L. Luo, and N. L. Wang, arXiv:0807.3137
  9. Z. Ren, W. Yue-Qin, and Z. Li-Chun, Chinese Phys. Lett. 25, 2385 (2008)
  10. M. Rotter, M. Tegel and D. Johrendt, Phys. Rev. Lett. 101, 107006 (2008); K. Sasmal, B. Lv, B. Lorenz, A. M. Guloy, F. Chen, Y.-Y. Xue, and C.-W. Chu, 101, 107007 (2008)
  11. Y. Mizuguchi, F. Tomioka, S. Tsuda, T. Yamaguchi, and Y. Takano, arXiv:0807.4315
  12. J. Dong, H. J. Zhang, G. Xu, Z. Li, G. Li, W. Z. Hu, D. Wu, G. F. Chen, X. Dai, J. L. Luo, Z. Fang, and N. L. Wang, Europhys. Lett. 83, 27006 (2008)
  13. T. Nomura, S. W. Kim, Y. Kamihara, M. Hirano, P. V. Sushko, K. Kato, M. Takata, A. L. Shluger, and H. Hosono, arXiv:0804.3569
  14. A. I. Goldman, D. N. Argyriou, B. Ouladdiaf, T. Chatterji, A. Kreyssig, S. Nandi, N. Ni, S. L. Bud’ko, P. C. Canfield, and R. J. McQueeney, arXiv:0807.1525v2
  15. Y. Qiu, W. Bao, Q. Huang, J. W. Lynn, T. Yildirim, J. Simmons, Y. C. Gasparovic, J. Li, M. Green, T. Wu, G. Wu, and X.H. Chen, arXiv:0806.2195
  16. J. Zhao, Q. Huang, C. de la Cruz, S. Li,J. W. Lynn, Y. Chen, M. A. Green, G. F. Chen, G. Li, Z. Li, J. L. Luo, N. L. Wang, and P. Dai, arXiv:0806.2528
  17. H. Luetkens, H.-H. Klauss, M. Kraken, F. J. Litterst, T. Dellmann, R. Klingeler, C. Hess, R. Khasanov, A. Amato, C. Baines, J. Hamann-Borrero, N. Leps, A. Kondrat, G. Behr, J. Werner, and B. Buchner, arXiv:0806.3533
  18. M. S. Torikachvili, S. L. Bud’ko, N. Ni, and P. C. Canfield, Phys. Rev. Lett. 101, 057006 (2008)
  19. A. Kreyssig, M. A. Green, Y. Lee, G. D. Samolyuk, P. Zajdel, J. W. Lynn, S. L. Bud’ko, M. S. Torikachvili, N. Ni, S. Nandi, J. Leao, S. J. Poulton, D. N. Argyriou, B. N. Harmon, P. C. Canfield, R. J. McQueeney, and A. I. Goldman, arXiv:0807.3032
  20. I. I. Mazin and M. D. Johannes, arXiv:0807.3737
  21. T. Yildirim, Phys. Rev. Lett. 101, 057010 (2008)
  22. T. Yildirim, arXiv:0807.3936
  23. D. J. Singh and M-H. Du, Phys. Rev. Lett. 100, 237003 (2008); D. J. Singh, arXiv:0807.2643
  24. Z. P. Yin, S. Lebègue, M. J. Han, B. P. Neal, S. Y. Savrasov, and W. E. Pickett, Phys. Rev. Lett. 101, 047001 (2008)
  25. C. Liu, T. Kondo, M. E. Tillman, R. Gordon, G. D. Samolyuk, Y. Lee, C. Martin, J. L. McChesney, S. Bud’ko, M. A. Tanatar, E. Rotenberg, P. C. Canfield, R. Prozorov, B. N. Harmon, and A. Kaminski, arXiv:0806.2147
  26. S. E. Sebastian, J. Gillett, N. Harrison, C. H. Mielke, S. K. Goh, P. H. C. Lau, and G. G. Lonzarich, arXiv:0806.4726
  27. H. Ding et al., Europhys. Lett. 83, 47001 (2008); L. Zhao, H. Liu, W. Zhang, J. Meng, X. Jia, G. Liu, X. Dong, G. F. Chen, J. L. Luo, N. L. Wang, W. Lu, G. Wang, Y. Zhou, Y. Zhu, X. Wang, Z. Zhao, Z. Xu, C. Chen, and X. J. Zhou, arXiv:0807.0398; T. Kondo, A. F. Santander-Syro, O. Copie, C. Liu, M. E. Tillman, E. D. Mun, J. Schmalian, S. L. Bud’ko, M. A. Tanatar, P. C. Canfield, and A. Kaminski, arXiv:0807.0815
  28. T. Y. Chen, Z. Tesanovic, R. H. Liu, X. H. Chen, and C. L. Chien, Nature 453, 1224 (2008)
  29. C. Martin, R. T. Gordon, M. A. Tanatar, M. D. Vannette, M. E. Tillman, E. D. Mun, P. C. Canfield, V. G. Kogan, G. D. Samolyuk, J. Schmalian, and R. Prozorov, arXiv:0807.0876
  30. Yusuke Nakai, Kenji Ishida, Yoichi Kamihara, Masahiro Hirano, and Hideo Hosono, J. Phys. Soc. Jpn. 77, 073701 (2008); H-J. Grafe, D. Paar, G. Lang, N. J. Curro, G. Behr, J. Werner, J. Hamann-Borrero, C. Hess, N. Leps, R. Klingeler, and B. Büchner, Phys. Rev. Lett. 101, 047003 (2008)
  31. D. Parker, O. V. Dolgov, M. M. Korshunov, A. A. Golubov, and I. I. Mazin, arXiv:0807.3729; A. V. Chubukov, D. Efremov, and I. Eremin, arXiv:0807.3735
  32. L. Boeri, O. V. Dolgov, and A. A. Golubov, Phys. Rev. Lett. 101, 026403 (2008)
  33. A. D. Christianson, M. D. Lumsden, O. Delaire, M. B. Stone, D. L. Abernathy, M. A. McGuire, A. S. Sefat, R. Jin, B. C. Sales, D. Mandrus, E. D. Mun, P. C. Canfield, J. Y. Y. Lin, M. Lucas, M. Kresch, J. B. Keith, B. Fultz, E. A. Goremychkin, and R. J. McQueeney, arXiv:0807.3370; M. Zbiri, H. Schober, M. R. Johnson, S. Rols, R. Mittal, Y. Su, M. Rotter, and D. Johrendt, arXiv:0807.4429
  34. I. I. Mazin, D. J. Singh, M. D. Johannes, and M. H. Du, Phys. Rev. Lett. 101, 057003 (2008)
  35. M. M. Korshunov and I. Eremin, arXiv:0804.1793; T. A. Maier and D. J. Scalapino, Phys. Rev. B 78, 020514 (2008)
  36. C. W. Hicks, T. M. Lippman, K. A. Moler, M. E. Huber, Z. A. Ren, and Z. X. Zhao, arXiv:0807.0467
  37. A. D. Christianson, E. A. Goremychkin, R. Osborn, S. Rosenkranz, M. D. Lumsden, C. D. Malliakas, I. S. Todorov, H. Claus, D. Y. Chung, M. G. Kanatzidis, R. I. Bewley, and T. Guidi, arXiv:0807.3932
  38. P. A. Lee and X.-G. Wen, arXiv:0804.1739
  39. X. Dai, Z. Fang, Y. Zhou, and F-C. Zhang, Phys. Rev. Lett. 101, 057008 (2008); Q. Si and E. Abrahams, 101, 076401 (2008); X.-L. Qi, S. Raghu, C.-X. Liu, D. J. Scalapino, and S.-C. Zhang, arXiv:0804.4332; K. Seo, B. A. Bernevig, and J. Hu, arXiv:0805.2958; F. Wang, H. Zhai, Y. Ran, A. Vishwanath, and D.-H. Lee, arXiv:0805.3343
  40. S. Raghu, X-L. Qi, C-X. Liu, D. J. Scalapino, and S-C. Zhang, Phys. Rev. B 77, 220503 (2008)
  41. C. Cao, P. J. Hirschfeld, and H-P. Cheng, Phys. Rev. B 77, 220506 (2008)
  42. P. W. Anderson, Science 235, 1196 (1987)
  43. T. Sato, S. Souma, K. Nakayama, K. Terashima, K. Sugawara, T. Takahashi, Y. Kamihara, M. Hirano, and H. Hosono, J. Phys. Soc. Jpn. 77, 063708 (2008)
  44. M. C. Boyer, K. Chatterjee, W. D. Wise, G. F. Chen, J. L. Luo, N. L. Wang, E. W. Hudson, arXiv:0806.4400; O. Millo, I. Asulin, O. Yuli, I. Felner, Z.-A. Ren, X.-L. Shen, G.-C. Che, and Z.-X. Zhao, arXiv:0807.0359
  45. A. Dubroka, K. W. Kim, M. Rössle, V. K. Malik, A. J. Drew, R. H. Liu, G. Wu, X. H. Chen, and C. Bernhard, Phys. Rev. Lett. 101, 097011 (2008); J. Yang, D. Huvonen, U. Nagel, T. Room, N. Ni, P. C. Canfield, S. L. Bud’ko, J. P. Carbotte, and T. Timusk, arXiv:0807.1040
  46. H. Eisaki, N. Kaneko, D. L. Feng, A. Damascelli, P. K. Mang, K. M. Shen, Z-X. Shen, and M. Greven, Phys. Rev. B 69, 064512 (2004)
  47. H. Takahashi, K. Igawa, K. Arii, Y. Kamihara, M. Hirano, and H. Hosono, Nature 453, 376 (2008)

About the Author

Image of Michael R. Norman

Michael Norman is an Argonne Distinguished Fellow and also a Fellow of the American Physical Society. He was on the Editorial Board of Physical Review B from 2000 to 2005 and is currently on the Editorial Board of Physical Review X. Michael got his Ph.D. in physics in 1983 at Tulane University, Louisiana. After a postdoc on electronic structure, he turned to many body theory, working primarily on superconductivity. His other interests include spin liquids, magnetism, quantum criticality, and the interpretation of spectroscopic data in correlated electron systems. In 2008 he was recognized as an Outstanding Referee by the American Physical Society.

Subject Areas

Superconductivity

Related Articles

Superconductivity Experts Speak Up for Hydride Research
Superconductivity

Superconductivity Experts Speak Up for Hydride Research

An independent analysis of data on the hotly debated superconductivity of certain hydrogen-rich compounds, or hydrides, concludes that the phenomenon is likely genuine. Read More »

Making Waves in the Debate over Light-Induced Superconductivity
Superconductivity

Making Waves in the Debate over Light-Induced Superconductivity

New experiments with cuprate materials explore a connection between so-called charge-density waves and a light-induced state that resembles superconductivity. Read More »

Simulating Superconductivity in Optical Lattices
Atomic and Molecular Physics

Simulating Superconductivity in Optical Lattices

Researchers have devised a way to use atoms in optical lattices to model high-temperature superconductors, whose behavior is not yet fully understood. Read More »

More Articles