How to silence a one-ton bell

Miles Blencowe

Viewpoint

How to silence a one-ton bell

Department of Physics & Astronomy, Dartmouth College, Hanover NH 03755.

July 14, 2008• Physics 1, 3

The longitudinal ringing mode of a metal bar resonator weighing approximately one metric ton has been cooled to submillikelvin temperatures with the use of active amplifier feedback. Further improvements may allow researchers to approach the quantum limit for cooling macroscopic objects.

Figure caption — **Figure 1:** (Top) The AURIGA gravity wave detector consists of a 3 m long one-metric-ton aluminum bar that is in thermal contact with a liquid helium reservoir. Distant energetic events such as orbiting binary stars produce gravitational waves that cause the bar to expand and contract longitudinally; these displacements are measured by a low-noise detector. Vinante *et al.* used feedback cooling to reduce the temperature of the longitudinal mode to less than 1 mK. (Bottom) The resonator is represented schematically as an effective mass m on a spring (a harmonic oscillator with angular frequency $ω$ ) modeling a single mode of a mechanical resonator. This vibrational mode is coupled to a heat reservoir at temperature $T_{1}$ and to the input of a mass position detector (amplifier), where the amplifier back action behaves as a heat bath with some effective noise temperature $T_{A}$ and damping rate $γ_{A}$ . If the output of the amplifier is phase-shifted and added back into the amplifier input, a much lower resonator temperature is possible.

Quantum phenomena dominate the world of the very small, but researchers have long sought quantum signatures in the dynamics of macroscopic mechanical objects. One example is the search for superpositions of different center-of-mass position states, meaning that an object is quite literally in two places at once [1]. A common view holds that the demonstration of macroscopic quantum behavior is a matter of practicability; macroscopic superposition states are difficult to detect because they are destroyed extremely rapidly by unavoidable interactions with the environment [2]. Others suggest that some unknown wave-function collapse mechanism prevents the formation of macroscopic superposition states, so that such states cannot be demonstrated even in principle [3].

In recent years, advances in ultrasensitive measurement techniques have fueled interest in putting these views to the test. This has brought together three largely disconnected communities working in the areas of low-temperature solid-state electronics, quantum optics, and gravity wave detection. In the 1970s and 1980s, the gravity wave community pioneered practical quantum measurement theory [4], but the information now flows both ways. For example, schemes that serve the goals of quantum computing might also catch the faint vibrations of a massive resonator driven by an incident gravity wave. Such techniques are now being adapted to attempt the verification of quantum behavior in macroscopic mechanical systems. In a paper in Physical Review Letters [5], the AURIGA gravity wave detector team in Padova, Italy, report a significant step in this direction by cooling the 900 Hz fundamental longitudinal vibrational mode of their detector, a one-metric-ton aluminum alloy bar resonator, from a starting temperature of 4.2 K, down to 0.2 mK. The 900 Hz fundamental mode of the detector is closer to its ground state than has ever been achieved in such a massive object.

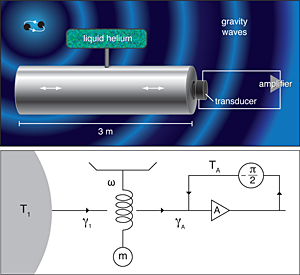
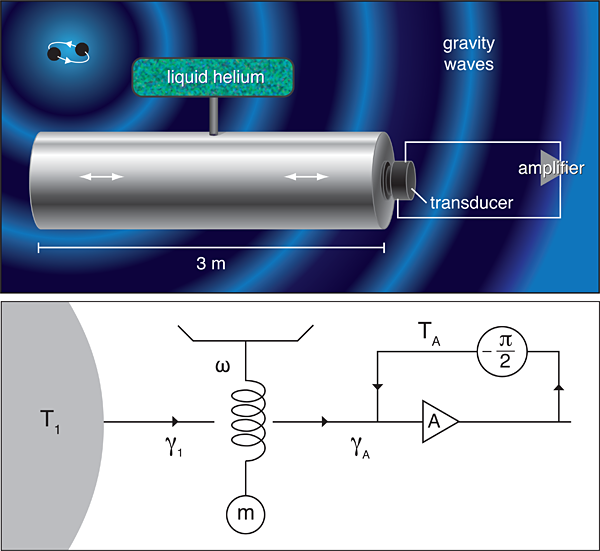
Detectors such as AURIGA are essentially immense but precisely machined tuning forks that are designed to quiver when excited by gravitational waves from distant cataclysmic events (e.g., the merger of black holes). AURIGA is a huge cylindrical bar equipped with vibration sensors and cooled by thermal contact with liquid helium to remove background noise (see Fig. 1, top) and can in principle vibrate at its fundamental frequency long after the gravity wave has passed.

To observe quantum behavior in a given vibrational mode of a mass resonator, which behaves approximately as an harmonic oscillator, it is necessary to cool the mode to close to its ground state: $k_{B} T / ħ ω \sim 1$ , where $T$ is the temperature of the surrounding bath and $ω$ is the frequency of the mode. The AURIGA team was able to push this ratio down to about 4000, corresponding to the thermal average number of energy quanta stored in the mode. This number is about two orders of magnitude larger than the current cooling and detection record of about 25 vibrational energy quanta [6]. In the latter experiment, the fundamental bending motion of a solid-state resonator was cooled in a liquid helium dilution fridge down to about 30 mK. However, that resonator weighed only $\sim 10^{- 15}$ kg; the AURIGA bar is eighteen orders of magnitude more massive, making their cooling of this detector all the more impressive an achievement.

How did the AURIGA team manage to cool the fundamental longitudinal mode of their one-ton bar resonator below a millikelvin? The basic elements of their cooling method are a sufficiently large longitudinal mode quality factor $Q$ and a very sensitive amplifier that measures the end-face displacements of the vibrating bar at the longitudinal mode frequency. Recall that the $Q$ of a given vibrational mode is defined in terms of the energy damping rate $γ$ and angular frequency $ω$ as $Q = ω / γ$ , so that large $Q$ ’s correspond to low damping rates. Consider a mechanical oscillator mode that is in thermal contact with two separate heat baths, one at temperature $T_{1}$ (e.g., the cryogenic liquid) and the other (e.g., some device to remove energy) at a temperature $T_{2} < T_{1}$ . In order to determine the steady-state temperature $T_{m}$ of the mechanical oscillator, we equate the rate at which the oscillator absorbs heat from the bath at the higher temperature $T_{1}$ with the rate at which the oscillator emits heat to the lower temperature $T_{2}$ bath. The thermal conductances of the heat flow pathways are directly proportional to the respective $γ$ ’s, thus $T_{m} = (γ_{1} / γ_{m}) T_{1} + (γ_{2} / γ_{m}) T_{2}$ , where $γ_{m} = γ_{1} + γ_{2}$ is the mechanical oscillator’s net damping rate. From this expression, we immediately see that in order to cool the oscillator towards the lower temperature $T_{2}$ bath, we necessarily require that $γ_{2} ≫ γ_{1}$ , or equivalently for the quality factors: $Q_{2} ≪ Q_{1}$ .

One way to thermally couple the resonator to a lower temperature bath relies on the fact that the back action on a mechanical oscillator caused by the displacement detector amplifier can behave effectively like a coupled heat bath [7]. In particular, the amplifier damps the mechanical oscillator with some rate $γ_{A}$ and exerts an accompanying random-noise force on the oscillator, characterized by some effective temperature $T_{A}$ . An amplifier can have a much lower effective temperature than the ambient bath; remember that amplifiers are inherently nonequilibrium systems, so no law of thermodynamics is being violated. Furthermore, the damping rate $γ_{A}$ can be much larger than that due to the coupling of the oscillator to its ambient bath, so amplifier back action can cool a mechanical oscillator. Recent demonstrations of this include radiation pressure cooling of (sub)millimeter scale mechanically compliant mirrors [8], and the above-mentioned solid state experiment [6], which also showed how to cool a micrometer scale mechanical resonator using the back action of tunneling Cooper pairs in a superconducting single-electron transistor displacement detector.

Figure 1 (bottom) illustrates the cooling method employed by the AURIGA team. In the experiment, the resonator oscillations moved the plates of a capacitor, which induced current flow in a magnetic coil, and the magnetic signal was detected by a low-noise superconducting quantum interference device (SQUID) with negligible back action on the mechanical oscillator. In contrast with the passive back action-cooling method, it is the amplified mechanical signal and added noise output fed back into the intermediate signal circuitry stage that provides the much lower temperature $T_{A}$ effective heat bath. The damping force is produced by cleverly shifting the phase of the output signal by $- π / 2$ before feeding back [9]. Thus, feeding back this output signal provides the desired viscous damping force with damping rate $γ_{A}$ proportional to the amplifier gain. A simple analogy would be a child’s swing: pushing on the swing exactly out of phase will gradually reduce the swing oscillations. Other recent experiments have used optical radiation pressure feedback to cool much smaller mass mechanical mirror resonators down to millikelvin temperatures [10].

The intermediate signal circuitry between the one-ton bar resonator and SQUID amplifier in fact includes two additional coupled oscillators in series, one a much smaller few kilogram mass mechanical oscillator and the other a superconducting electrical $L C$ oscillator with an even smaller effective “mass” of a few grams, both nearly resonant with the 900 Hz fundamental longitudinal bar mode and with comparable Q factors of about $10^{6}$ . The coupled oscillators also increase the detection bandwidth that would otherwise be limited by the damping rate of the fundamental bar mode ( $\sim 0.01 s^{- 1}$ ). This is potentially of use for the detection of gravity waves. However, it must be stressed that neither passive back action nor active feedback cooling of the fundamental mode can improve the detection sensitivity of gravity waves, which is limited by the net force noise on the oscillator mass. In particular, the net force noise scales as the product of the net energy damping rate and the steady-state temperature, i.e., $γ_{m} T_{m}$ , which remains unaffected because a decrease in $T_{m}$ (i.e., cooling) is offset by a corresponding increase in $γ_{m}$ . One possible advantage for detection, however, is that by increasing the net damping rate of the detector, the bandwidth is increased, which is useful for detecting shorter timescale gravity wave signals.

This cooling milestone represents significant progress toward the demonstration of quantum behavior in macroscopic mechanical objects. A potentially interesting follow-up experiment might involve switching off the feedback once the fundamental mode is in its cooled steady state, and then monitoring the mode dynamics as it warms back up to the ambient temperatures. Such an investigation will help provide a better understanding of the mechanical energy damping mechanisms at these cryogenic temperatures. This is a poorly understood subject and yet is essential to realizing the eventual goal of watching a macroscopic quantum superposition state evolve into a classical mixture of either-or alternatives.

Acknowledgments

I thank G. Milburn and R. Onofrio for helpful feedback and also the NSF (grant CMS0404031) for their support.

References

Keith C. Schwab and Michael L. Roukes, Phys. Today 58, 36 (2005)
Wojciech H. Zurek, Phys. Today 44, 36 (1991)
L. Diósi, Phys. Rev. A 40, 1165 (1989); G. Ghirardi, R. Grassi, and A. Rimini, 42, 1057 (1990); Roger Penrose, Gen Relat Gravit 28, 581 (1996)
C. M. Caves, K. S. Thorne, R. W. P. Drever, V. D. Sandberg, and M. Zimmermann, Rev. Mod. Phys. 52, 341 (1980); V. B. Braginsky and F. Ya. Khalili Quantum Measurement (Cambridge University Press, Cambridge, 1992) [Amazon][WorldCat]
A. Vinante et al., Phys. Rev. Lett. 101, 033601 (2008)
A. Naik, O. Buu, M. D. LaHaye, A. D. Armour, A. A. Clerk, M. P. Blencowe, and K. C. Schwab, Nature 443, 193 (2006)
H. Hirakawa, S. Hiramatsu, and Y. Ogawa , Phys. Lett. 63A, 199 (1977); B. Braginsky and S. P Vyatchanin , Phys. Lett. A 293, 228 (2002)
Constanze Höhberger Metzger and Khaled Karrai, Nature 432, 1002 (2004); S. Gigan, H. R. Böhm, M. Paternostro, F. Blaser, G. Langer, J. B. Hertzberg, K. C. Schwab, D. Bäuerle, M. Aspelmeyer, and A. Zeilinger, 444, 67 (2006); O. Arcizet, P.-F. Cohadon, T. Briant, M. Pinard, and A. Heidmann, 444, 71 (2006); A. Schliesser, P. Del’Haye, N. Nooshi, K. J. Vahala, and T. J. Kippenberg, Phys. Rev. Lett. 97, 243905 (2006); J. D. Thompson, B. M. Zwickl, A. M. Jayich, Florian Marquardt, S. M. Girvin, and J. G. E. Harris, Nature 452, 72 (2008)
S. Mancini, D. Vitali, and P. Tombesi, Phys. Rev. Lett. 80, 688 (1998)
Dustin Kleckner and Dirk Bouwmeester, Nature 444, 75 (2006); M. Poggio, C. L. Degen, H. J. Mamin, and D. Rugar, Phys. Rev. Lett. 99, 017201 (2007); T. Corbitt, C. Wipf, T. Bodiya, D. Ottaway, D. Sigg, N. Smith, S. Whitcomb, and N. Mavalvala, 99, 160801 (2007)

About the Author

Miles Blencowe received his B.Sc. (1986) and Ph.D. (1989) degrees in theoretical physics at Imperial College. He subsequently held postdoctoral fellowships at the University of Cambridge (1989-1991), the University of Chicago (1991-1993), and the University of British Columbia (1993-1994). Following a senior research associate position at Imperial College (1994-1999), he moved to Dartmouth College where he is currently an associate professor in the Department of Physics and Astronomy. His research interests lie in the areas of mesoscopic physics, quantum information theory applied to solid-state systems, and non-equilibrium statistical mechanics.

Feedback Cooling of the Normal Modes of a Massive Electromechanical System to Submillikelvin Temperature

A. Vinante, M. Bignotto, M. Bonaldi, M. Cerdonio, L. Conti, P. Falferi, N. Liguori, S. Longo, R. Mezzena, A. Ortolan, G. A. Prodi, F. Salemi, L. Taffarello, G. Vedovato, S. Vitale, and J.-P. Zendri

Phys. Rev. Lett. 101, 033601 (2008)

Published July 14, 2008

Read PDF