New clues in the mystery of persistent currents

Hélène Bouchiat

Viewpoint

New clues in the mystery of persistent currents

Laboratoire de Physique des Solides Université Paris-Sud, Bldg. 510, Orsay Cedex, France 91405

July 28, 2008• Physics 1, 7

A decade ago, experimentalists showed that persistent currents can flow in nonsuperconducting mesoscopic metal rings, but there was no theory that correctly explained the magnitude or direction of the unexpectedly large currents. Theorists are now proposing a simple idea that may at last explain these results.

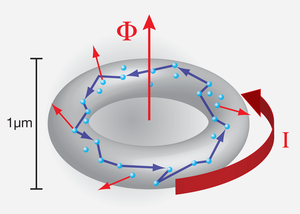
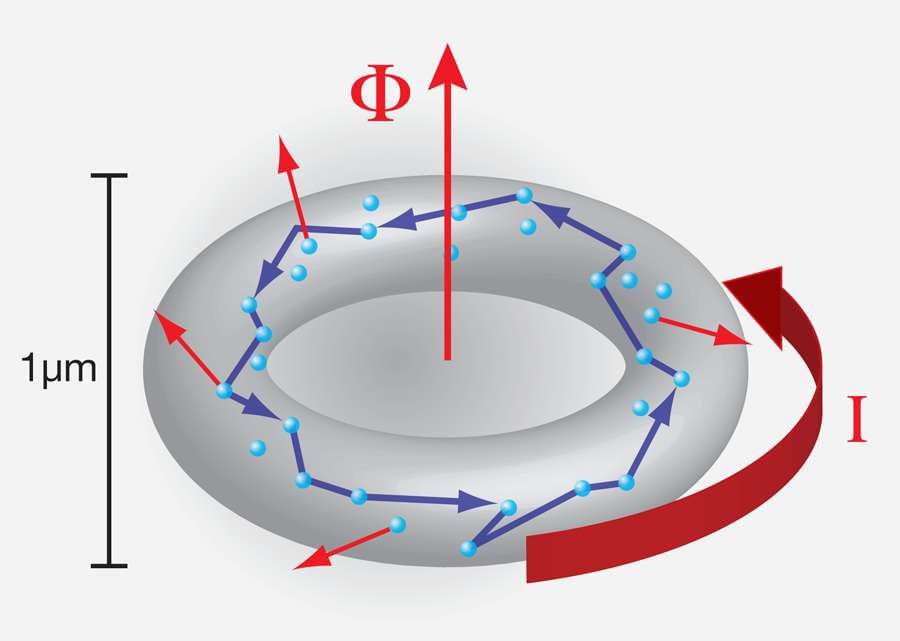
Figure caption — **Figure 1:** Schematic representation of a persistent current in a mesoscopic metal ring threaded by a magnetic flux quantum, $Φ$ . For rings $\sim 1 μ m$ in size and at a temperature $T \sim 1 K$ , the flux quantum induces a persistent current due to the Aharonov-Bohm effect. Elastic scattering from static impurities (light blue spheres) does not destroy the phase coherence of the wave functions and persistent currents can flow even though the metal has a finite resistance. The phase coherence of the electron waves is more sensitive to spin-flip scattering from magnetic impurities (red arrows). However, while a concentration of 1 ppm magnetic impurities would be enough to destroy superconductivity in these metal rings, it is not sufficient to quench persistent currents in the normal state.

If we apply a voltage pulse to a wire, we know that the current that starts to flow will eventually disappear. This is because electrons scatter inelastically from phonons and other electrons as they flow through most metals, eventually losing all of their energy. However, in metal rings that are smaller than the electron’s phase coherence length—the typical distance the electron travels before it scatters inelastically—it is possible to induce currents that last forever simply by threading the center of the ring with a magnetic flux (Fig. 1) [1]. Until now, the size of these persistent currents, as well as how their direction depends on the orientation of the central flux, has been a mystery. Now, in a paper appearing this week in Physical Review Letters, Hamutal Bary-Soroker, Ora Entin-Wohlman, and Yoseph Imry at the Weizmann Institute in Israel propose a solution to this problem that is so simple, yet compelling, that physicists may wonder why no one has thought of it before [2].

The existence of persistent (i.e., with no energy dissipation) diamagnetic currents on macroscopic scales has been considered a hallmark of superconductivity in metals ever since its discovery in 1911. Persistent currents in superconductors are related to the existence of a state with zero resistance and the fact that a superconductor is a perfect diamagnet (it opposes the applied field). More than seventy years later, in 1983, Büttiker, Landauer, and Imry pointed out that persistent currents should also exist in nonsuperconducting (“normal”) metallic loops threaded by magnetic flux [3]. To observe these dissipationless currents, the temperature must be sufficiently low to reduce the probability of inelastic scattering (from phonons and other electrons) and the circumference of the ring short enough that the phase coherence of the electronic wave functions is preserved around the loop. This typically limits the sample size to a micrometer or so, and the temperature to below 1 K. These persistent currents can be seen as the analogue, albeit on a much greater scale, to the orbital currents in aromatic ring molecules, such as benzene, that give rise to a molecular magnetic moment.

The existence of persistent currents in normal metals is, in fact, a signature of phase coherence in mesoscopic systems and an example of the famous Aharonov-Bohm effect. For a magnetic flux $Φ$ threading the loop, the electronic wave function (over the closed loop) acquires a phase proportional to $e / ħ Φ$ . Since the electronic wave function must be continuous around the loop, the amplitude of the current will adjust so that the acquired phase is an integer multiple of $2 π$ . As a result, the amplitude of the persistent current is a periodic function of the magnetic flux quantum, $Φ_{0} = h / e \sim 4.14 \times 10^{- 15} T m^{2}$ (in SI units; note that for superconductors, the flux quantum is $Φ_{0} = h / 2 e$ because the electrons are paired). The maximum amplitude of the current is of the order $e / τ_{D}$ where $τ_{D}$ is the typical time for an electron to travel around the ring. This yields a current of the order of $1 \times 10^{- 9} A$ . The magnitude of the current is independent of the cross-sectional area of the ring and is thus much smaller than the persistent current in a superconducting ring of similar dimensions, since the latter results from a coherent motion of all charge carriers condensed in a macroscopic coherent state. Disorder, which gives rise to elastic scattering, reduces, but does not completely destroy, the persistent current in a normal-state metal ring. This means that persistent currents exist in rings that have a finite resistance: if you connect one of these rings to a current generator, the generator will have to do work to push a current through, and, differently from a superconductor, one cannot measure a drop in resistance. Rather, it is only by measuring the very small induced magnetic moment associated with the circulating current that the persistent current can be revealed.

Another fundamental trait of persistent currents in normal rings, which distinguishes them from superconducting persistent currents, is that the direction of the induced current depends on the number of electrons in the ring as well as the details of the disorder potential [3,4]. In contrast, persistent currents in superconducting rings (at low enough fields) are always diamagnetic.

For all these reasons detection of persistent currents has long been considered an experimental challenge. The moment from an individual ring corresponds to about $100 μ_{B}$ (Bohr magnetons), which is at the sensitivity limit of the best magnetic detectors (recall that the magnetic moment from a single spin is given by $m = μ_{B} g S$ ). Unfortunately, an ensemble measurement with many rings could not overcome this low signal problem, because each ring was expected to contribute a moment with a random sign. This belief prevailed until it was shown theoretically that if one considers the effects of electron-electron interactions, the ensemble average of persistent currents taken on many rings would not be zero (even though for any individual ring, the sign of the current is random). This ensemble average was also shown to have a $Φ_{0} / 2$ periodicity, half the periodicity of the persistent currents in a single ring, and an average current per loop of $0.05 e / τ_{D}$ [5]. The average sign of the currents was found to depend on the nature of the interactions: for repulsive interactions, the prediction was that the induced current would generate a moment along the direction of the applied field, while for attractive interactions, a diamagnetic response was expected.

Inspired by these predictions, the first experiment was performed in the early 1990s by measuring the magnetization of an array of about ten million disconnected, micron-sized copper rings [6]. The magnetic signal was, as expected, periodic in $Φ_{0} / 2$ , but the amplitude corresponded to an average ring current of $0.3 e / τ_{D}$ , more than five times the theoretical predictions. More surprising, the magnetization was found to be diamagnetic at low magnetic flux. This suggested that attractive electron-electron interactions were important. Attractive interactions between electrons are normally mediated by phonons—the same effect that leads to superconductivity in many simple metals. Yet the mesoscopic rings were made of metals in which the superconducting transition temperature was so low it did not seem possible that phonon interactions were strong enough to lead to such large persistent currents. Copper, for example, has not been found to superconduct, even at temperatures as low as $10 μ K$ ! How could attractive interactions in copper be so weak that they would not lead to superconductivity at measurable temperatures, but still permit a large persistent current in the normal state?

Bary-Soroker et al.’s solution to this longstanding puzzle of persistent currents is amazingly simple. They consider the role played by a tiny amount of magnetic impurities, of the order of one part per million (1 ppm), which unavoidably exists in any metal. Magnetic impurities give rise to spin-flip scattering, which is one of the most efficient mechanisms that destroy superconductivity. If $1 / τ_{S}$ is the rate at which this spin scattering occurs, then as soon as $ħ / τ_{S}$ rises to the order of $k_{B} T_{c}$ (where $T_{c}$ is the superconducting transition temperature), superconductivity is destroyed. This happens when the concentration of magnetic impurities is approximately 1 ppm for a $T_{c} \sim 1 mK$ . Bary-Soroker et al. suggest that without these pernicious magnetic impurities, superconductivity would occur in pure copper at a transition temperature $T_{c 0}$ of the order of $1 mK$ – about three orders of magnitude higher than the currently estimated upper bound for $T_{c}$ in copper. Now, spin-flip scattering also limits the coherence length, $L_{s}$ , of electrons in the normal state of a metal to $L_{s} = (D τ_{S})^{1 / 2}$ , where $D$ is the diffusion coefficient. But $L_{s}$ is still of the order of $10 μ m$ for 1 ppm of magnetic impurities. Thus 1 ppm of magnetic impurities is enough to destroy bulk superconductivity in copper, but it has much less of an effect on the phase coherence in micron size rings. This is the case, provided that the metal is at a low enough temperature for which inelastic phase breaking times such as electron-phonon or electron-electron scattering times are longer than $τ_{S}$ .

The group’s ideas show that the sign and amplitude of the ensemble average persistent current is determined by the amplitude of the attractive electron-electron interaction, that is, the electron-electron interaction that corresponds to a superconducting transition of the order of $1 mK$ (instead of $10 μ K$ as initially believed). The attractive interaction leads to diamagnetic persistent currents, with an amplitude of the order of $e / τ_{D}$ , the value measured for persistent currents in copper.

These theoretical findings provide for the first time a complete explanation for the sign and amplitude of persistent currents in mesoscopic rings. But these results will do much more than close the door on a long-standing question. They will likely stimulate new experiments. It is possible, for example, to test these predictions by investigating rings made from known low- $T_{c}$ materials in which a controlled number of magnetic impurities have been added. Another possibility could be to measure the amplitude of persistent currents in rings made of bilayer materials such as Al/Cu in which the transition temperature can continuously be decreased by decreasing the thickness of the aluminum layer. With such a system, it would be possible to reach a regime where the transition temperature of the bilayer becomes too low to be measurable, but is still known theoretically. Finally, since experiments on mesoscopic rings remain challenging, these results could pave the way to the theoretical investigation of other signatures of pair breaking in mesoscopic rings in the normal state, such as magnetic field dependent transport.

Acknowledgments

We thank Sophie Guéron and Gilles Montambaux for valuable comments on the manuscript.

References

Y. Imry, Introduction to Mesoscopic Physics[Amazon][WorldCat] 2nd ed. (Oxford University Press, Oxford, 2002).
H. Bary-Soroker, O. Entin-Wohlman and Y. Imry, Phys. Rev. Lett. 101, 057001 (2008)
M. Büttiker, Y. Imry, and R. Landauer, Physics Letters A 96, 365 (1983)
H-F. Cheung, E. K. Riedel, and Y. Gefen, Phys. Rev. Lett. 62, 587 (1989)
A. Schmid, Phys. Rev. Lett. 66, 80 (1991); V. Ambegaokar and U. Eckern, 67, 3192 (1991)
L. P. Lévy, G. Dolan, J. Dunsmuir, and H. Bouchiat, Phys. Rev. Lett. 64, 2074 (1990)

About the Author

Hélène studied at Ecole normale supérieure (1977–1981) and completed her Ph.D. (1981–1986) at the Laboratoire de Physique des Solides, Université Paris Sud, in Orsay. From 1987 to 1988 she was a consultant for Bell Laboratories. In 1988 she returned to the Laboratoire de Physique des Solides, where she is now Directeur de Recherche. Her present research interests include the study of quantum transport in mesoscopic systems and carbon nanotubes and low temperature molecular electronics.