Watching the Hoyle State Fall Apart

Oliver Kirsebom

Viewpoint

Watching the Hoyle State Fall Apart

Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, Aarhus C Denmark, 8000

September 25, 2017• Physics 10, 103

Two experiments provide the most precise picture to date of how an excited state of carbon decays into three helium nuclei.

Figure caption — **Figure 1:** Nuclear models predict that the Hoyle state of carbon-12 can break apart into its three constituent alpha particles either in two steps (left) or, much more rarely, all at once. In the two-step process, an alpha particle—two neutrons (green) and two protons (blue)—is emitted, leaving a beryllium-8 nucleus that quickly decays into two alpha particles. Smith *et al.* [1] and Dell’Aquila *et al.* [2] have put the most stringent limit to date on the percentage of decays that occur in the direct manner.

We are used to picturing atomic nuclei as smooth and spherical distributions of neutrons and protons. But the reality is often very different, and the carbon-12 nucleus provides the perfect case in point. In its ground state and some of its excited states, carbon’s six neutrons and six protons are thought to segregate into three clusters of two neutrons and two protons, otherwise known as helium nuclei or alpha particles. Two experimental teams have now performed measurements that will help explore key details of this alpha-cluster model. Robin Smith and colleagues at the University of Birmingham, UK [1], and Daniele Dell’Aquila of the University of Naples Federico II, Italy, and colleagues [2] analyzed the breakup of an excited state of carbon-12, known as the Hoyle state, into three alpha particles. The teams’ measurements are sufficiently sensitive that they might be used to confirm recent model predictions about the Hoyle state, which is relevant to the nucleosynthesis of carbon in stars. Their results could also be used to probe certain parameters of the alpha-cluster model.

In the 1920s, before the discovery of the neutron, physicists speculated that alpha particles were the fundamental constituents of atomic nuclei—a reasonable guess for the time, given that many radioactively decaying nuclei emit alpha particles. Researchers eventually realized that the building blocks of nuclei are, in fact, neutrons and protons. But the alpha-cluster model has survived as a useful effective theory, capable of describing numerous nuclei and their excited states.

Appreciation for the importance of alpha clustering came in the 1950s, when physicists were struggling to explain the nucleosynthesis of carbon-12 in the Universe. The leading idea was that carbon-12 is produced via the so-called triple-alpha reaction in stars, in which two alpha particles fuse into beryllium-8 and then capture a third alpha particle to form carbon-12. However, the predicted reaction rate was more than 7 orders of magnitude too low to produce the abundance of carbon in the solar system.

The astrophysicist Fred Hoyle solved this problem in 1953, when he showed that this reaction would run forward much more quickly if the beryllium-8’s capture of the third alpha particle resulted in a short-lived excited state of carbon-12, which subsequently relaxes to the carbon-12 ground state. The Hoyle state was soon observed in experiments at the excitation energy Hoyle had predicted. Although the standard shell model of nuclear physics failed to predict the Hoyle state, a 1956 model put forth by Haruhiko Morinaga successfully described it in terms of three weakly interacting alpha particles [3]. Morinaga's crude model has since been greatly refined, but its essential feature—an alpha-clustered structure—has largely been verified in experiments [4].

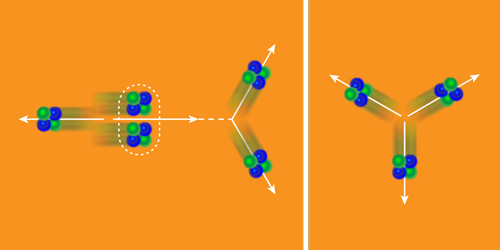
However, researchers continue to debate and test the specifics of the alpha-cluster model, such as the degree of clustering and whether the alpha particles are configured in a linear chain, a bent arm, or a triangle [5]. The experiments by Smith et al. and Dell’Aquila et al. concern the specific manner in which the Hoyle state decays into its three constituent alpha particles—a possible decay path that is different from the relaxation to the carbon ground state mentioned previously. In 2014, theorists [6] predicted that 99.9% of such decays occur through an indirect two-step process in which the Hoyle state first emits one alpha particle, and then the beryllium-8 nucleus left behind breaks up into two more alpha particles (Fig. 1, left). Only in 0.1% of cases would the breakup proceed more directly and form three alpha particles at once (Fig. 1, right).

The experiments by Smith et al. and Dell’Aquila et al. [1, 2] have, for the first time, reached the level of sensitivity needed to test the 2014 prediction quantitatively, thereby providing a check on the alpha-cluster model’s accuracy. To do so, both teams adopted established strategies for efficiently preparing a population of nuclei in the Hoyle state: Smith et al. produced them from a nuclear reaction between nitrogen and deuterium, while Dell’Aquila et al. utilized a reaction between carbon and helium. The decays through the two-step and one-step processes are difficult to distinguish: in the two-step process, the delay between the emission of the first alpha particle and the breakup of the beryllium-8 is only about $1 0^{- 16} s$ —too short to measure. Luckily, the sequential and direct breakups can be distinguished by how the energy is shared between the alpha particles and the relative orientation of the alpha particles as they fly apart. Earlier experiments differentiated the two decay paths using special detectors that had high energy and spatial resolution and that could assign precise time stamps to each detected alpha particle. The new experiments go a step further by designing detection systems that can determine the directions of the alpha particles with increased confidence, especially in those cases where two alpha particles have very similar energies.

While previous experimenters managed to establish that at most 0.2% of decays are direct (with 95% confidence), the new experiments have, with the same confidence, succeeded in pushing this limit down to 0.04%. At first sight, the improved upper limit appears to conflict with the theoretical prediction of 0.1%. But this discrepancy mostly goes away if the predictions take into account the experimental resolution, leading to a revised predicted limit of 0.05%.

What will we do with this newly available comparison between theory and experiment? The agreement between experiment and theory is marginal, so even a two- to threefold improvement in the experimental sensitivity would be of significant interest. Reaching this seemingly modest improvement will, however, likely require new measurement techniques that go beyond the conventional spectroscopy used by Smith et al. and Dell’Aquila et al., such as taking advantage of the near-perfect detection efficiency of active-target detectors [7].

Nuclear theorists also need to figure out whether their calculations are as accurate as they appear. This pursuit should include a careful investigation of the sensitivity of the alpha-cluster model to various assumptions—in particular, to the model’s description of the alpha-alpha interaction. Theorists should also attempt to calculate the breakup pathways using microscopic models that consider all 12 nucleons in the carbon nucleus [8], though such calculations are notoriously difficult.

We may ultimately discover that the breakup process isn’t highly sensitive to the nuclei’s initial structure and is instead mainly determined by the interactions between the alpha particles in the final state. Even in this case, improved measurements would still be an important check on calculations of the triple-alpha reaction in low-temperature stellar environments [9, 10].

This research is published in Physical Review Letters.

References

R. Smith et al., “New Measurement of the Direct 3 $𝛼$ Decay from the $^{12}$ C Hoyle State,” Phys. Rev. Lett. 119, 132502 (2017).
D. Dell'Aquila et al., “High-Precision Probe of the Fully Sequential Decay Width of the Hoyle State in $^{12}$ C,” Phys. Rev. Lett. 119, 132501 (2017).
H. Morinaga, “Interpretation of Some of the Excited States of 4n Self-Conjugate Nuclei,” Phys. Rev. 101, 254 (1956).
M. Chernykh, H. Feldmeier, T. Neff, P. von Neumann-Cosel, and A. Richter, “Structure of the Hoyle State in $^{12}$ C,” Phys. Rev. Lett. 98, 032501 (2007).
M. Freer and H.O.U. Fynbo, “The Hoyle State in $^{12}$ C,” Prog. Part. Nucl. Phys. 78, 1 (2014).
S. Ishikawa, “Decay and Structure of the Hoyle State,” Phys. Rev. C 90, 061604 (2014).
T. Ahn et al., “The Prototype Active-Target Time-Projection Chamber used with TwinSol Radioactive-Ion Beams,” Nucl. Instrum. Methods Phys. Res. B 376, 321 (2016).
M. Freer, H. Horiuchi, Y. Kanada-En'yo, D. Lee, and U.-G. Meißner, “Microscopic Clustering in Nuclei,” arXiv:1705.06192.
H. Suno, Y. Suzuki, and P. Descouvemont, “Three-alpha Radiative Reaction Processes at Low Temperatures,” JPS Conf. Proc. 14, 020405 (2017).
S. Ishikawa, “Three-body Calculations of the Triple- $𝛼$ Reaction,” Phys. Rev. C 87, 055804 (2013).

About the Author

Oliver Kirsebom obtained a Ph.D. in physics in 2010 from Aarhus University in Denmark. He then spent three years as a postdoctoral researcher at TRIUMF in Canada before returning to Aarhus University, where he is now an assistant professor on a grant from the Villum Foundation. Oliver performs experiments at various accelerator laboratories, including ISOLDE, in Switzerland, and JYFL, in Finland, to better understand light atomic nuclei and their role in nucleosynthesis and the energy generation in stars. Some of his most recent research has been concerned with alpha clustering in relation to carbon production in stars.