Scattering Atoms Catch the d Wave
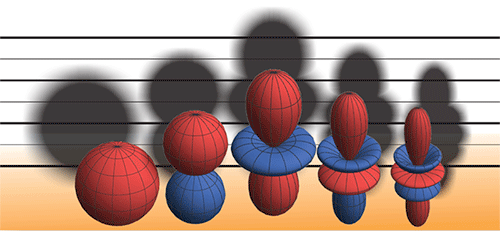
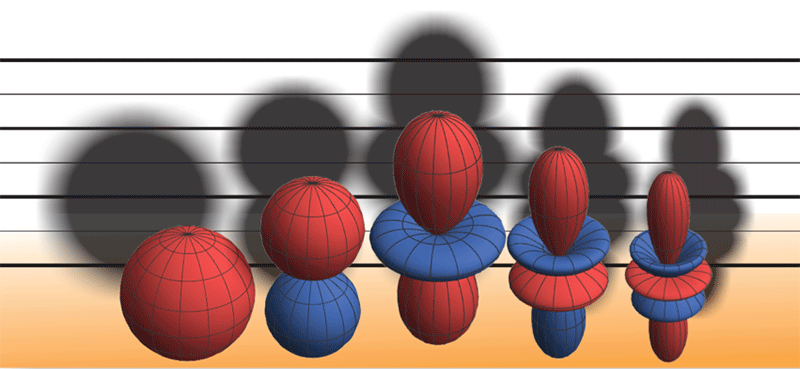
Gases of ultracold atoms provide an exquisite platform for exploring models of condensed-matter physics. The atoms, which act as stand-ins for electrons or other degrees of freedom in solids and fluids, can be controlled by researchers with great finesse, allowing atomic systems to simulate exotic forms of magnetism, quantum phase transitions, and other traditionally condensed-matter phenomena. However, simulating high-temperature superconductivity has been a tougher nut to crack, since the electrons in this phase experience a particular pairwise interaction that is spatially anisotropic. This so-called d-wave (Fig. 1) [1] interaction is difficult to emulate with atoms at suitably low temperatures. Working with ultracold rubidium atoms, a team led by Li You at Tsinghua University, China, has succeeded in creating the desired d-wave interactions at low temperatures by using a magnetic field to induce a scattering resonance between the atoms [2]. Unlike electrons, which are fermions, the atoms the team works with are bosons—an important distinction. Nonetheless, the new work provides an essential ingredient to begin exploring simulations of high-temperature superconductivity as well as other many body phases that involve d-wave interactions.
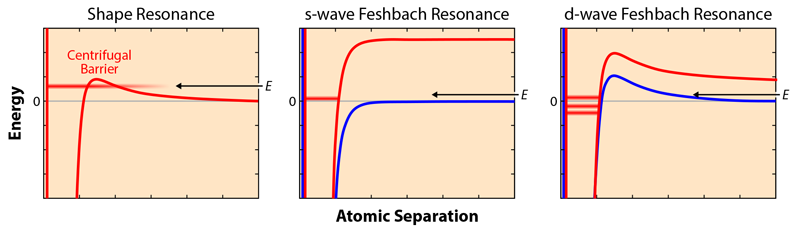
Resonances can make a spectacular imprint on the quantum-mechanical encounter between two atoms [3]. At a resonance, the collision energy of the particles is close to the energy they would have in a molecular-like quasibound state. When this happens, the scattering between the atoms may change dramatically, and the effective atom-atom interaction can, for example, be greatly enhanced, completely extinguished [4], or change from being isotropic to anisotropic [5].
A particularly simple setting for a resonance is two free particles in relative angular motion. In this case, the motion creates a centrifugal barrier between the free particles and a metastable molecular state (Fig. 2, left). The barrier is analogous to the classical effect that prevents an orbiting planet from falling into its sun, except that quantum mechanics allows the particles to tunnel through the barrier. Resonances associated with centrifugal barriers are called shape resonances, and because they stem from the particles’ relative angular motion, they are labeled p, d, and so on, where p corresponds to 1 unit of quantized orbital angular momentum, d to 2 units, and so on. Similarly, the angular distribution of the scattering particles is described as p wave, d wave, etc. (Fig. 1). Shape-resonance experiments have observed p-wave- and d-wave-dominated scattering patterns in potassium-40 [5] and rubidium-87 [6], respectively. In these cases, the atoms exhibit the anisotropic interactions one might aim for in order to simulate condensed-matter systems. Unfortunately, shape resonances typically occur at atom-gas temperatures of order a few hundred microkelvin, while nanokelvin temperatures are required for atom gases to properly simulate solids. Such low temperatures ensure that the atom wavelength is on par with the separation between the atoms, a condition that often applies to the electrons of interest in solids.
In their work, You and his colleagues push the regime for d-wave-dominated atom interactions to suitably low temperatures by exploiting so-called Feshbach resonances [7]. Like shape resonances, Feshbach resonances rely on a coupling between free particles and a molecular-like state. In the Feshbach case, however, the atoms in the molecular state have different spin states than the incoming ones, which means an external magnetic field can be used to shift the molecule’s energy with respect to the free particles.
Working with a mixture of two rubidium isotopes (rubidium-85 and rubidium-87), You and co-workers use a magnetic field to create a d-wave Feshbach resonance. Specifically, they tune the field to bring the energy of a molecular state in line with that of free particles whose collision energy is close to zero, thus enabling the resonance at low temperatures. Such field-aligned Feshbach resonances have been widely used to enhance the isotropic, or s-wave, scattering of atoms (Fig. 2, center). Similarly, researchers have demonstrated Feshbach resonances in which the free particles are s wave and the molecular state is d wave (or vice versa). But to fully capture d-wave interactions as they would occur in solids, one needs a direct coupling between d-wave free particles and d-wave molecular states. You’s team achieves this scenario (Fig. 2, right) for the first time by following an earlier prediction by co-author Bo Gao [8], who explained how to prepare the internal states of the atoms and what field to use in order to obtain the desired resonance.
In their experiment, the researchers prepare their 25- 𝜇K mixture according to Gao’s recipe and then load it into a trap formed by two crossed laser beams. They then proceed to lower the temperature by dimming the trapping beam to let the most energetic atoms escape. To identify a Feshbach resonance, the researchers sweep the magnetic field and look for an uptick in the loss of atoms from the trap, an expected outcome of enhanced atom-atom interactions. At 400 nK, they observe three loss “peaks” at around 423 G, the telltale number of features for a genuine d-wave to d-wave resonance. The researchers also affirm that the resonance can be categorized as “broad,” which means the resonance has a simplified description that is independent of the detailed properties of the atoms themselves—exactly what one needs to cleanly control atom interactions when simulating condensed-matter systems.
With genuine and broad d-wave interactions in hand, what more could we want? Well, in order to simulate a condensed-matter system, the atoms need to stick around, so it’s essential to find resonances that don’t eject too many atoms out of the trap. Fortunately, You’s team has identified just such a resonance at 620 G. Here, both types of rubidium atoms start out in their absolute spin ground states, so two colliding atoms can’t gain kinetic energy by flipping their spins. But even if the system were run at 620 G, the researchers would still have to tackle three-body losses, in which two atoms form a molecule while a third assists in carrying away the energy gained. You’s team envisages suppressing the three-body interactions by placing the rubidium mixture in an optical lattice formed by interfering laser beams. This setup will allow them to study the many-body physics of an atomic mixture with Feshbach tunable interactions [9], with the added exciting possibility of exploring the effects of d-wave-dominated couplings.
This research is published in Physical Review Letters.
References
- C. C. Tsuei and J. R. Kirtley, “Phase-Sensitive Tests of Pairing Symmetry in Cuprate Superconductors,” in Superconductivity Vol. II: Novel Superconductors, edited by K. H. Bennemann and J. B. Ketterson (Springer, Berlin, 2008)[Amazon][WorldCat].
- Y. Cui, C. Shen, M. Deng, S. Dong, C. Chen, R. Lü, B. Gao, M. K. Tey, and L. You, “Observation of Broad d-Wave Feshbach Resonances with a Triplet Structure,” Phys. Rev. Lett. 119, 203402 (2017).
- V. I. Kukulin, V. M. Krasnapol’sky, and J. Horácěk, Theory of Resonances: Principles and Applications (Springer, Berlin, 1989)[Amazon][WorldCat].
- R. K. Adair, C. K. Bockelman, and R. E. Peterson, “Experimental Corroboration of the Theory of Neutron Resonance Scattering,” Phys. Rev. 76, 308 (1949).
- R. Thomas, K. O. Roberts, E. Tiesinga, A. C. J. Wade, P. B. Blakie, A. B. Deb, and N. Kjærgaard, “Multiple Scattering Dynamics of Fermions at an Isolated p-Wave Resonance,” Nat. Commun. 7, 12069 (2016).
- N. Kjærgaard, A. S. Mellish, and A. C. Wilson, “Differential Scattering Measurements from a Collider for Ultracold Atoms,” New J. Phys. 6, 146 (2004).
- C. Chin, R. Grimm, P. Julienne, and E. Tiesinga, “Feshbach Resonances in Ultracold Gases,” Rev. Mod. Phys. 82, 1225 (2010).
- B. Gao, “Analytic Description of Atomic Interaction at Ultracold Temperatures. II. Scattering Around a Magnetic Feshbach Resonance,” Phys. Rev. A 84, 022706 (2011).
- Th. Best, S. Will, U. Schneider, L. Hackermüller, D. van Oosten, I. Bloch, and D.-S. Lühmann, “Role of Interactions in 87Rb−40K Bose-Fermi Mixtures in a 3D Optical Lattice,” Phys. Rev. Lett. 102, 030408 (2009).