Quantum Spin Torque
Magnetoresistive random access memories (MRAMs)—a promising memory storage technology based on spintronics—store bits of information in spin valves consisting of junctions of two magnetic layers. To write data in a MRAM junction, a magnetic field switches the magnetization of one of the two layers. Recently, researchers started to explore a variation of the technique based on the spin-transfer torque (STT), an effect in which the layer magnetization isn’t switched by a magnetic field but by a spin-polarized current. Compared to conventional MRAMs, a memory based on STT would consume less power and feature better scalability. The interest for applications has driven intense research efforts in the field, but our present understanding of STT is still incomplete. Now, Andrei Zholud [1] of Emory University, Georgia, and his colleagues have found that a classical model can’t explain spin transport phenomena observed in a spin valve. Specifically, their experiments indicate that at low temperatures, the effect of STT on the quantum fluctuations of the magnetization is remarkably different than the effect it has on thermal fluctuations. The result calls for an improvement of STT models through the inclusion of quantum effects.
John Slonczewski and Luc Berger first proposed the STT effect in 1996 [2] as a novel mechanism for switching magnetization with an electric current. Its experimental realization in spin-valve trilayers (cobalt-copper-cobalt) came in 2000 [3]. Since then, research has rapidly expanded to various magnetic materials and nanostructures. The physical description of STT, however, has remained qualitatively the same for all the investigated systems. In a spin valve, a current passing through a magnetic layer (usually called the “fixed” layer) becomes spin polarized. After passing through a nonmagnetic layer, the current is directed into the second magnetic layer, or “free” layer. If the magnetizations of the two magnetic layers are not parallel, the spin-polarized current can be absorbed by the free layer [4]. This absorption transfers some angular momentum, exerting a torque that can change the free layer’s magnetization, causing its direction to either oscillate or switch completely.
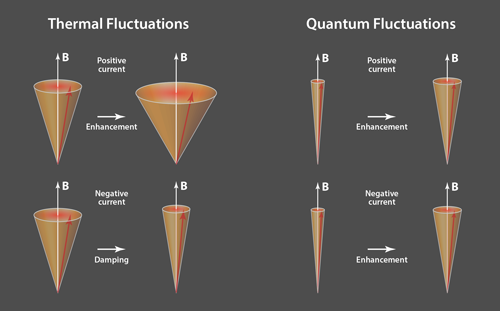
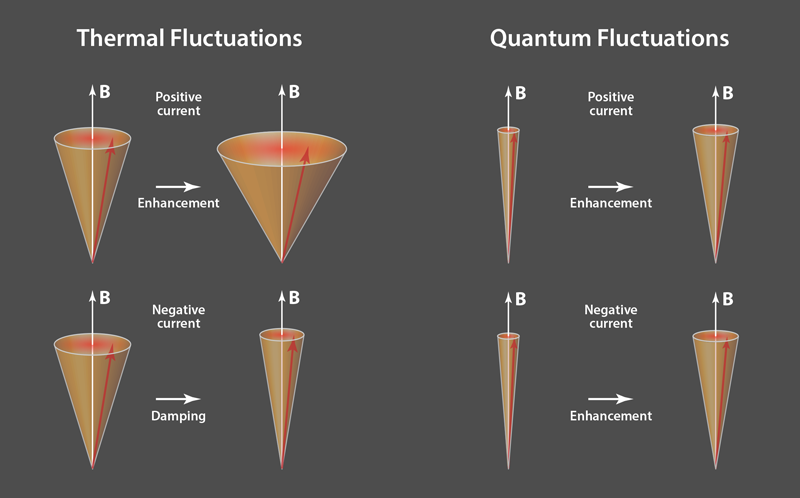
The effect of STT is dependent on the direction of the current—a property that is the basis for STT-based MRAM devices. If current flows from the fixed to the free layer, STT competes with the magnetic damping torque that naturally tends to align the magnetization of the free layer to that of the fixed layer. For such current direction, the STT is an antidamping torque [see Fig. 1(a)]. In the opposite current direction, the STT increases the magnetic damping and becomes an overdamping torque, which further contributes to aligning the two layers. In a device, the free-to-fixed and the fixed-to-free directions can make the magnetization of the free layer parallel and antiparallel to the fixed layer, respectively. This STT phenomenology can be theoretically described by adding an additional torque term to the classical Landau-Lifshitz-Gilbert equations. In such a formalism, the magnetization of the free layer is approximated as a classical vector that is subject to thermal fluctuations. Up until now, this approach has successfully explained a vast range of experimental data, mostly obtained at room temperature.
In such a classical picture, thermal fluctuations affect the magnetization by creating a random magnetic field whose magnitude is proportional to the temperature and the damping parameter. The effect of STT can be described as an additional term that affects the damping parameter. Hence, one would predict—based on the so-called fluctuation-dissipation theorem—that an antidamping STT would amplify the magnetization fluctuations. On the other hand, when STT is overdamping, it would reduce such fluctuations. This behavior has been previously confirmed both theoretically [5] and experimentally at room temperature [6].
What happens, however, when quantum effects become more prominent? To answer this question, Zholud et al. investigated the effect of STT on magnetic fluctuations at cryogenic temperatures. At these low temperatures, thermal fluctuations are suppressed, allowing the effect of quantum fluctuations to be observed. Since quantum fluctuations are the minimum fluctuations governed by the uncertainty principle, neither the STT nor an applied magnetic field can reduce their magnitude. By measuring the resistance of the samples as a function of the electric current, Zholud et al. found that the fluctuations are enhanced for both directions of the current at low temperature, as illustrated in Fig. 1(b). This behavior is remarkably different from that predicted by a classical model of STT.
In principle, the heating induced by the current propagating through the spin valve could be responsible for the enhanced fluctuations found for both directions of the current. The authors, however, rule out heating as the cause, based on the observed current-dependence of the fluctuation enhancement: Joule heating would lead to a quadratic dependence on current, while the experiments reveal a linear dependence. The authors thus conclude that the quantum fluctuations are the origin for the observed phenomenon.
The observation that the quantum fluctuations are enhanced for both directions of the current indicates the failure of the current STT model, which predicts that the STT is an antidamping torque for one direction of the current and an overdamping torque for the other direction. The results raise several fundamental questions about the properties of the STT: What microscopic model can account for the enhanced quantum fluctuations? Will quantum effects at low temperatures affect other spin transport properties like spin pumping or the spin Hall effect? Will such quantum effects also be relevant for other important spintronic structures, such as, for instance, magnetic tunnel junctions? Further research will be needed to address these questions.
At present, research on STT remains mostly empirical and focused on developing devices that are optimal for spintronics applications: multilayer spin-valve structures that can be controlled using the smallest possible current at room temperature. The discovery by Zholud et al., however, may lead to important advances in the fundamental description of STT physics, which, in turn, may open new possibilities on the technological front.
This research is published in Physical Review Letters.
References
- A. Zholud, R. Freeman, R. Cao, A. Srivastava, and S. Urazhdin, “Spin Transfer due to Quantum Magnetization Fluctuations,” Phys. Rev. Lett. 119, 257201 (2017).
- J. C. Slonczewski, “Current-Driven Excitation of Magnetic Multilayers,” J. Magn. Magn. Mater. 159, L1 (1996); L. Berger, “Emission of Spin Waves by a Magnetic Multilayer Traversed by a Current,” Phys. Rev. B 54, 9353 (1996).
- J. A. Katine, F. J. Albert, R. A. Buhrman, E. B. Myers, and D. C. Ralph, “Current-Driven Magnetization Reversal and Spin-Wave Excitations in Co/Cu/Co Pillars,” Phys. Rev. Lett. 84, 3149 (2000).
- M. D. Stiles and A. Zangwill, “Anatomy of Spin-Transfer Torque,” Phys. Rev. B 66, 014407 (2002).
- Z. Li and S. Zhang, “Thermally Assisted Magnetization Reversal in the Presence of a Spin-Transfer Torque,” Phys. Rev. B 69, 134416 (2004).
- R. H. Koch, J. A. Katine, and J. Z. Sun, “Time-Resolved Reversal of Spin-Transfer Switching in a Nanomagnet,” Phys. Rev. Lett. 92, 088302 (2004).