Microwave Quantum States Beat the Heat
From microwave ovens to satellite television to the GPS and data services on our mobile phones, microwave technology is everywhere today. But one technology that has so far failed to prove its worth in this wavelength regime is quantum communication that uses the states of single photons as information carriers. This is because single microwave photons, as opposed to classical microwave signals, are extremely vulnerable to noise from thermal excitations in the channels through which they travel. Two new independent studies, one by Ze-Liang Xiang at Technische Universität Wien (Vienna), Austria, and colleagues [1] and another by Benoît Vermersch at the University of Innsbruck, also in Austria, and colleagues [2] now describe a theoretical protocol for microwave quantum communication that is resilient to thermal and other types of noise. Their approach could become a powerful technique to establish fast links between superconducting data processors in a future all-microwave quantum network.
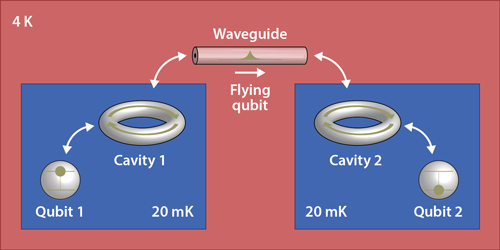
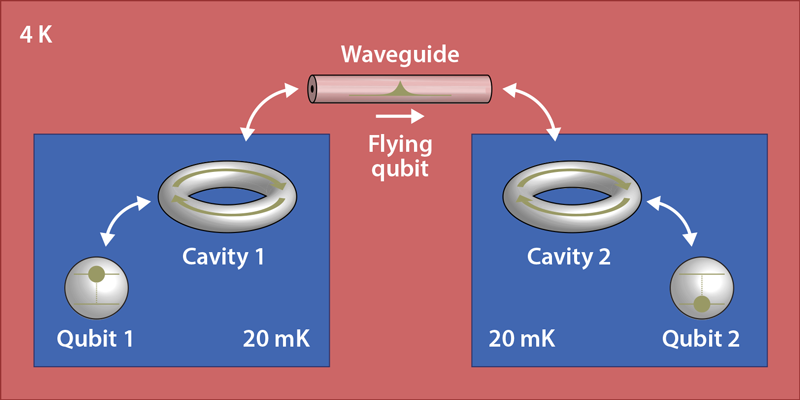
Interest in building quantum information and communication technologies based on microwave photons was triggered by pioneering quantum electrodynamics experiments in microwave cavities [3]. And it was quickly boosted by a newfound ability to control the microwave quantum states of superconducting qubits and photons on the chip scale, both inside cavities [4] and waveguides [5]. But the prevailing view has since been that microwave quantum states are doomed to remain within the confines of expensive and bulky liquid-helium dilution refrigerators; these instruments are required to cool the devices that host these fragile quantum systems to a temperature of about 20 mK, at which thermal excitations are largely absent. Xiang and colleagues and Vermersch and colleagues now show that this need not be the case by developing a protocol that can transfer such states through a communication channel cooled to only about 4 K using comparatively cheap liquid-helium cooling infrastructure (Fig. 1).
To understand their protocol, consider a quantum communication network made of just two distant nodes, each consisting of a superconducting qubit placed inside a dilution refrigerator. Consider further that qubit 1 is prepared in an excited quantum state of choice and qubit 2 is in the ground state, and that one seeks to transfer the excited state of qubit 1 to qubit 2 via a channel such as a low-loss waveguide. Previous protocols [6] showed that it is possible to achieve this transfer with high fidelity by carefully controlling the temporal shape of a “flying” photonic qubit in the waveguide. Unfortunately, however, this scheme works only if the waveguide is devoid of any electromagnetic noise.
Xiang and colleagues and Vermersch and colleagues realized that if the two stationary qubits are not directly coupled to the flying qubit but are instead each connected to an intermediary linear harmonic oscillator, such as a microwave cavity, the state transfer becomes immune to noise in the waveguide. This can be achieved as follows. First, the state of qubit 1 is mapped onto a superposition state of oscillator 1. Second, the stationary qubits and their respective oscillators are decoupled from one another, and a state transfer between the two oscillators is implemented via the flying qubit. Third, the coupling between oscillators and qubits is reinstated, and the state of oscillator 2 is mapped onto that of qubit 2. The researchers show that careful time-domain control of the oscillator–waveguide coupling in the second step results in a perfect cancellation between the noise that is first absorbed and then emitted by oscillator 1 and the noise that drives oscillator 2 directly. This cancellation relies only on the strict linear nature of the two oscillators. What’s more, the authors also show that the two oscillators can be used to partly correct [7] for state-transfer errors caused by photon loss and absorption in the waveguide.
The two groups arrived at this protocol from different directions. Xiang and colleagues did so by using an analytical method to find a robust state-transfer scheme for superconducting qubits. Vermersch and colleagues employed a numerical technique to study the dynamics of the state transfer in photonic and phononic networks. Both approaches allowed them to carefully investigate the sensitivity of the derived protocol to errors associated with photon loss and absorption, as well as to imperfections in the time-domain control of the oscillator-waveguide coupling.
Xiang and colleagues predict that high-fidelity transfer can be realized for channels up to a few tens of meters long at a temperature of 4 K, using high-quality 3D superconducting cavity technology like that originally developed for particle accelerators [8]. Moreover, with the fast tunable coupling rate of superconducting qubits to flying microwave qubits [9], the new protocol could enable deterministic exchange of quantum information at a rate of up to – qubits per second, which is difficult to achieve with current optical technology. Maintaining a high speed of data transfer in distributed quantum networks, like the ones the two Austrian groups have studied, will be essential. That’s because distributed quantum processing may be the only way to handle the very large number of superconducting qubits required for fault-tolerant quantum simulation of hard-to-crack problems in materials science and quantum chemistry [10].
This research is published in Physical Review X and Physical Review Letters.
References
- Z.-L. Xiang, M. Zhang, L. Jiang, and P. Rabl, “Intracity Quantum Communication via Thermal Microwave Networks,” Phys. Rev. X 7, 011035 (2017).
- B. Vermersch, P.-O. Guimond, H. Pichler, and P. Zoller, “Quantum State Transfer via Noisy Photonic and Phononic Waveguides,” Phys. Rev. Lett. 118, 133601 (2017).
- S. Haroche and J. M. Raimond, Exploring the Quantum: Atoms, Cavities, and Photons (Oxford University Press, Oxford, 2006)[Amazon][WorldCat].
- M. Hofheinz et al., “Synthesizing Arbitrary Quantum States in a Superconducting Resonator,” Nature 459, 546 (2009).
- C. Eichler, C. Lang, J. M. Fink, J. Govenius, S. Filipp, and A. Wallraff, “Observation of Entanglement between Itinerant Microwave Photons and a Superconducting Qubit,” Phys. Rev. Lett. 109, 240501 (2012).
- J. I. Cirac, P. Zoller, H. J. Kimble, and H. Mabuchi, “Quantum State Transfer and Entanglement Distribution among Distant Nodes in a Quantum Network,” Phys. Rev. Lett. 78, 3221 (1997).
- M. H. Michael, M. Silveri, R. T. Brierley, V. V. Albert, J. Salmilehto, L. Jiang, and S. M. Girvin, “New Class of Quantum Error-Correcting Codes for a Bosonic Mode,” Phys. Rev. X 6, 031006 (2016).
- J. P. Turneaure and I. Weissman, “Microwave Surface Resistance of Superconducting Niobium,” J. Appl. Phys. 39, 4417 (1968).
- J. Wenner et al., “Catching Time-Reversed Microwave Coherent State Photons with 99.4% Absorption Efficiency,” Phys. Rev. Lett. 112, 210501 (2014).
- M. Reiher, “Elucidating Reaction Mechanisms on Quantum Computers,” arXiv:1605.03590.