Photonic Hat Trick
Quantum interference effects lie at the heart of technologies that promise radically new capabilities for sensors, secure communications, and computing. Most existing experiments and applications rely on one photon interfering with itself, or two photons interfering with each other. However, the interference of a larger number of particles leads to a richer variety of phenomena, and may enable more sophisticated applications. Now, two independent groups, the first led by Thomas Jennewein at the University of Waterloo, in Canada [1], the second by Ian Walmsley at the University of Oxford, in the UK [2], have been able to isolate and observe, for the first time, “genuine” interference between three photons, that is, an effect deriving from the quantum interference of three photons that does not originate from two-photon or single-photon interference. The two studies provide new tools for controlling multiphoton interference, which may help researchers design new fundamental tests of quantum mechanics, quantum-communication protocols, and powerful quantum simulators.
The quintessential example of multiphoton quantum interference is the Hong-Ou-Mandel (HOM) effect, first observed in 1987. In an HOM experiment [3], two independent photons coming from different directions impinge on a 50:50 beam splitter. If the two incoming photons are distinguishable, the outgoing photons will split equally between the two exit ports of the splitter. However, if the two photons are identical and arrive simultaneously, the quantum-mechanical wave functions will interfere, and the two photons will always exit through the same port, even though each of them has an equal probability of exiting through both ports.
Today, researchers are increasingly addressing the richer physics accessible when more than two photons interfere. Already, the simplest extension to three photons would open up new applications. An intriguing one is three-photon quantum secret sharing [4], in which a secure quantum key is shared among three parties such that it can only be used by all three parties together, not by one or two of them alone. It’s a bit like sharing a joint bank account with two other holders but not being able to access it without everyone’s consent. Theoretical work has also shown that three-photon interferometry could help quantum sensing schemes beat the precision limits set by shot noise [5] or boost the efficiency of interaction-free measurements [6], which detect the state of a quantum particle without interacting with it.
Many groups have studied different forms of three- and multiphoton interference over the past 30 years. But none have so far been able to isolate and observe genuine interference beyond two photons. Doing so requires both exquisite control of the input photon quantum states and the design of an interferometeric setup that is able to eliminate all single- and two-photon interference contributions. The two new studies achieve such feats through simple and elegant experiments based on very different strategies.
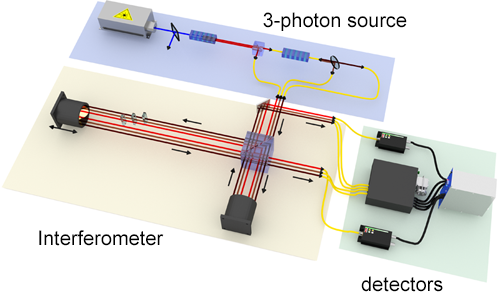
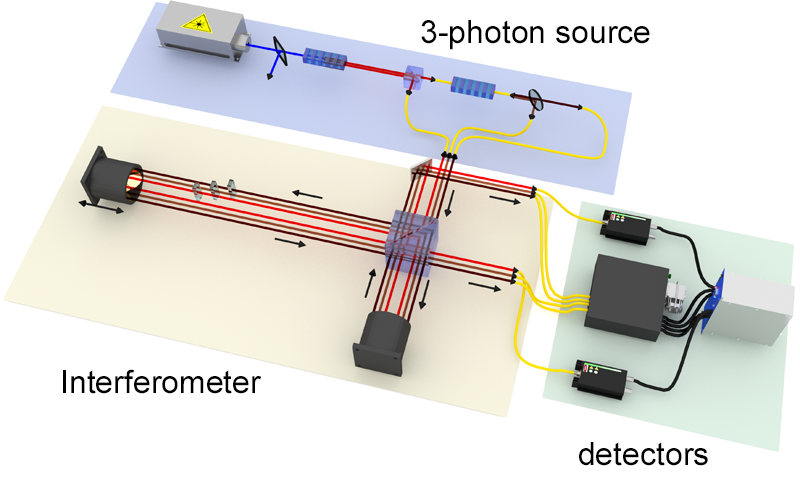
In the first paper, Jennewein and colleagues [1] follow closely a theoretical recipe proposed by Daniel Greenberger, Michael Horne, and Anton Zeilinger in 1993 [7], which relies on a single source that can emit a three-photon quantum state that has no independent entanglement between any two of the photons. Such a three-photon entangled state is key to observing genuine three-photon quantum interference in this experiment. This is a technological challenge because schemes for producing multiphoton states are very inefficient. Using a technique they pioneered [8], the team generates entangled states of three photons through the cascade of a nonlinear process called spontaneous parametric down-conversion (SPDC). In SPDC, a single high-energy pump photon is converted into two low-energy photons in a nonlinear crystal. In the cascaded version, one of the photons emitted by the first SPDC crystal pumps the same process in a second crystal, generating two additional photons. Because the sum of the energies of the three photons must equal the energy of the pump photon, the three photons that emerge from the cascaded source are correlated in both energy and time [9]. The efficiency of the authors’ source allows them to detect almost 200 photon triplets per hour, an increase by a factor of around 30 compared to previous experiments.
Each of the three photons then travels through one arm of an interferometer (Fig. 1), and is detected in one of two output ports. The probability that all three photons arrive simultaneously at the same output mode is proportional to the sum of the three phases picked up by the photons in the interferometer. By changing the phases for each photon using glass plates inside the interferometer, the authors observe oscillations in the rate of three-photon coincidences, while the rate of two-photon coincidences remains constant, a signature of genuine three-photon interference.
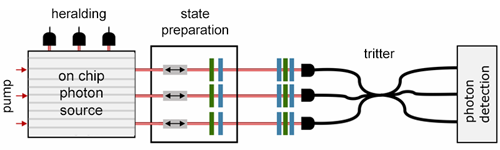
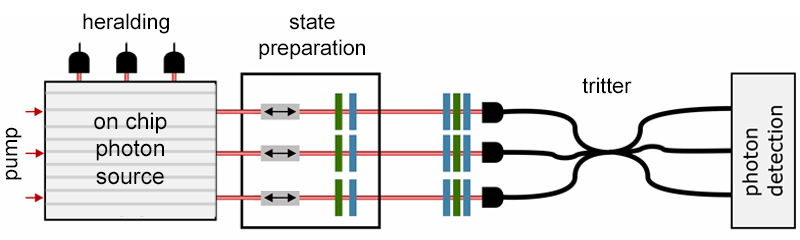
Walmsley and colleagues [2] follow a different approach, studying the three-photon analog of the HOM effect [3]. Their scheme (Fig. 2), which relies on technical advances developed by the group, integrates multiple near-identical SPDC sources within one photonic chip [10]. Instead of using three entangled photons generated in the same nonlinear process, the authors start with three independent photons generated by the separate SPDC sources. The photons are sent to an optical-fiber-based beam splitter with three inputs and three outputs, known as a tritter. The probability that all three photons exit from different ports depends on two key control parameters: the distinguishability of the photons, and a so-called triad phase, which, unlike in the two-photon case, is nonzero only if the three photons are partially, yet not fully, distinguishable.
The scheme’s efficiency allows the observation of photon triplets at a rate of around 200 events per hour. By varying each photon’s timing and polarization, the authors are able to control the photon distinguishability and the triad phase independently. When they do so, they observe the same effect as Jennewein's group: The three-photon coincidence rate varies sinusoidally with the triad phase, whereas the two-photon coincidence and single-photon count rates remain constant.
The step from two photons to three may not seem that important. But we have only just begun to climb the ladder of available multiphoton quantum states of light, and each step will bring surprises and possible new applications. The techniques developed by these groups may well become part of the standard toolbox of quantum optics, just as the Hong-Ou-Mandel effect has become a widely used tool for characterizing two-photon quantum states. Perhaps the most exciting possibility on the horizon is the use of multiphoton interferometers, similar to that developed by Walmsley's group, in boson-sampling devices, which calculate the probability with which bosons are scattered in a linear interferometer. The growing interest in such devices stems from the fact that they could be the first quantum machines capable of solving tasks that are intractable for classical computers [11]. The tools introduced by Walmsley and colleagues will be very useful for controlling photon distinguishability, which plays an important role in boson-sampling schemes [12].
This research is published in Physical Review Letters.
References
- S. Agne, T. Kauten, J. Jin, E. Meyer-Scott, J. Z. Salvail, D. R. Hamel, K. J. Resch, G. Weihs, and T. Jennewein, “Observation of Genuine Three-Photon Interference,” Phys. Rev. Lett. 118, 153602 (2017).
- A. J. Menssen, A. E. Jones, B. J. Metcalf, C. Tichy, S. Barz, W. S. Kolthammer, and I. A. Walmsley, “Distinguishability and Many-Particle Interference,” Phys. Rev. Lett. 118, 153603 (2017).
- C. K. Hong, Z. Y. Ou, and L. Mandel, “Measurement of Subpicosecond Time Intervals Between Two Photons by Interference,” Phys. Rev. Lett. 59, 2044 (1987).
- M. Hillery, V. Bužek, and A. Berthiaume, “Quantum Secret Sharing,” Phys. Rev. A 59, 1829 (1999).
- K. R. Motes, J. P. Olson, E. J. Rabeaux, J. P. Dowling, S. Jay Olson, and P. P. Rohde, “Linear Optical Quantum Metrology with Single Photons: Exploiting Spontaneously Generated Entanglement to Beat the Shot-Noise Limit,” Phys. Rev. Lett. 114, 170802 (2015).
- P. G. Kwiat, A. G. White, J. R. Mitchell, O. Nairz, G. Weihs, H. Weinfurter, and A. Zeilinger, “High-Efficiency Quantum Interrogation Measurements via the Quantum Zeno Effect,” Phys. Rev. Lett. 83, 4725 (1999); D. M. Greenberger, M. Horne, and A. Zeilinger, “Similarities and Differences Between Two-Particle and Three-Particle Interference,” Fortschr. Phys. 48, 243 (2000).
- D. M. Greenberger, M. A. Horne, and A. Zeilinger, “Multiparticle Interferometry and the Superposition Principle,” Phys. Today 46, 22 (1993).
- H. Hübel, D. R. Hamel, A. Fedrizzi, S. Ramelow, K. J. Resch, and T. Jennewein, “Direct Generation of Photon Triplets Using Cascaded Photon-Pair Sources,” Nature 466, 601 (2010).
- L. K. Shalm, D. R. Hamel, Z. Yan, C. Simon, K. J. Resch, and T. Jennewein, “Three-Photon Energy–Time Entanglement,” Nat. Phys. 9, 19 (2012).
- J. B. Spring et al., “Chip-Based Array of Near-Identical, Pure, Heralded Single-Photon Sources,” Optica 4, 90 (2017).
- S. Aaronson and A. Arkhipov, “The Computational Complexity of Linear Optics,” Proceedings of the Forty-Third Annual ACM Symposium On Theory Of Computing, STOC ’11 (ACM, New York, 2011), p. 333[Amazon][WorldCat].
- M. C. Tichy, “Sampling of Partially Distinguishable Bosons and the Relation to the Multidimensional Permanent,” Phys. Rev. A 91, 022316 (2015).