Celebrated Optical Trick Goes Vibrational
The Nobel-Prize-winning invention of the optical frequency comb—light whose spectrum contains a series of sharp, equally spaced peaks—has revolutionized the design of atomic clocks and other high-precision devices. Researchers have now created a phononic frequency comb, in which the spectrum of vibrations of a crystal follows the same pattern as the optical comb. The discovery confirms a recent theoretical prediction and could be useful for precision measurements that require a stable, low-frequency standard, such as those involving slow changes.
Optical frequency combs have dramatically simplified and improved precision time measurement, among other fields. One way to generate an optical frequency comb is by means of a “nonlinear” medium in which photons interact with each other to generate new photons at frequencies different from those of the initial photons. These effects can be exploited to create light whose spectrum contains a series of many equally-spaced frequencies.
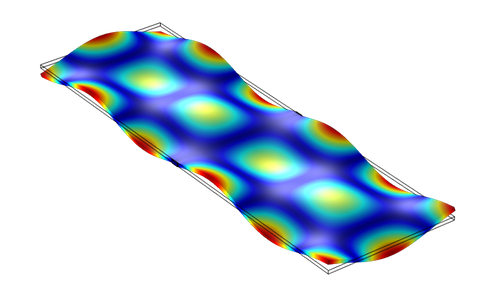
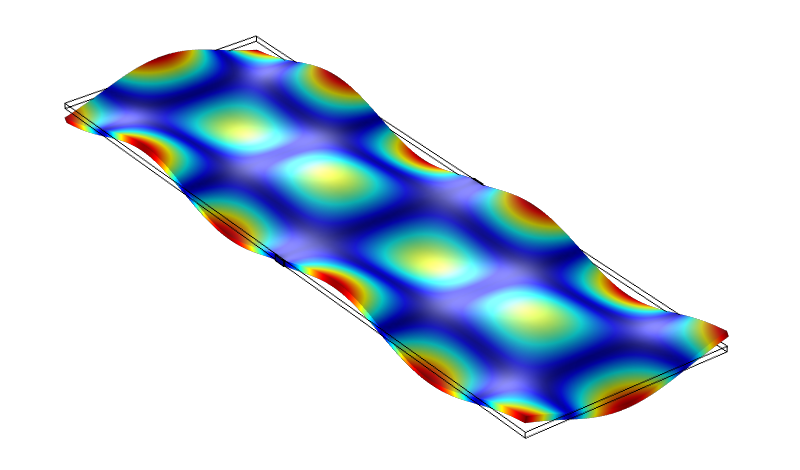
Ashwin Seshia and his colleagues at the University of Cambridge were not trying to create a phononic frequency comb, the vibrational equivalent of the optical comb. They were investigating the behavior of phonons—the vibrations of the atoms in a crystal structure—in a rectangular wafer of silicon, 1100 by 350 by 10 micrometers, covered by a thin layer of aluminum nitride, a material that vibrates in response to an applied voltage. The wafer was attached to a support structure at two points, allowing it to vibrate in response to an oscillating applied voltage. The team observed the wafer’s vibrations by reflecting laser light off of its surface, allowing them to record both the spatial pattern and the frequencies of phonons with high precision.
When they applied the oscillating voltage at certain frequencies, the researchers were surprised that the wafer’s response had the form of a frequency comb at locations on the surface with the largest amplitude of motion. For a stimulus frequency of 3.862 MHz, for example, the wafer’s vibration spectrum showed several peaks separated by 2.6 kHz.
Searching for an explanation for this surprising finding, the researchers came across a theoretical argument from 2014 depicting, in a schematic way, how to generate a phononic frequency comb [1]. Peter Schmelcher of the University of Hamburg, Germany, and his colleagues had studied so-called Fermi-Pasta-Ulam (FPU) chains—sets of masses connected by springs whose restoring force depends not just on the length by which they are stretched but also on the square and possibly the cube of that length. Vibrations of the chain represent one-dimensional phonons, and the nonlinearity allows these phonons to interact and create new phonons at different frequencies. Schmelcher and his colleagues showed that vibrating one end of an FPU chain at a forcing frequency that is slightly different from the sum of two resonant frequencies generates a frequency comb.
Seshia says that although the FPU model cannot capture the full complexity of phonon behavior in a wafer, he and his colleagues found that it accounted very well for the frequency combs they observed. As in the FPU model, it was important that the forcing frequency was not an exact sum of phonon frequencies of the wafer. When that condition was met, a comb spectrum arose with the spacing predicted by the theory. The variation of the comb response as the team varied the frequency and power of the forcing vibration also followed the FPU model.
The main experimental difficulty was that an off-resonance forcing frequency is inefficient at exciting phonons in the wafer: a frequency comb arose only when the power of the forcing oscillation exceeded a threshold value. However, Seshia says it should not be difficult to improve the design of the device to excite frequency combs more easily.
Schmelcher agrees that the new experiments verify the theoretical mechanism that he and his colleagues proposed. He also notes that since a frequency comb represents an additional set of phonons that can transmit vibrational energy in the wafer, it may open up new ways for a device to absorb vibrational energy and thus improve its efficiency.
Seshia sees possible applications in micro- and nano-electromechanical systems where the frequency interval of a comb would provide a precise and stable standard frequency much lower than the frequency of the phonons themselves. That could be especially valuable, he adds, for detecting changes on very long timescales, such as gravimeters that measure slow changes in the earth’s gravitational field.
This research is published in Physical Review Letters.
–David Lindley
David Lindley is a freelance science writer in Alexandria, Virginia.
References
- L. S. Cao, D. X. Qi, R. W. Peng, M. Wang, and P. Schmelcher, “Phononic Frequency Combs through Nonlinear Resonances,” Phys. Rev. Lett. 112, 075505 (2014).