How to Create a Time Crystal
The story of time crystals—whose lowest-energy configurations are periodic in time rather than space—epitomizes the creative ideas, controversy, and vigorous discussion that lie at the core of the scientific process. Originally theorized by Frank Wilczek in 2012 [1] (see 15 October 2012 Viewpoint), time crystals were met with widespread attention, but also a healthy dose of skepticism [2]. This ignited a debate in the literature, culminating in a proof that time crystals cannot exist in thermal equilibrium, as originally imagined by Wilczek [3]. But the tale did not end there. It was later argued that time crystals might still be possible in periodically driven systems, which can never reach thermal equilibrium [4–6]. Three recent papers have now completed the story, one proposing a roadmap for creating a nonequilibrium time crystal in the lab [7], and two describing subsequent experimental demonstrations in systems of trapped ions [8] and spin impurities in diamond [9] (both posted on the physics arXiv preprint server).
Empty space exhibits continuous translation symmetry: nothing distinguishes one point from any other. Yet ordinary crystals break this symmetry because atoms are periodically arranged in specific locations and display long-range spatial correlations. Given that we live in four-dimensional spacetime, it is natural to wonder if an analogous process of crystallization and symmetry breaking can arise along the time dimension as well [1]. If it does, then any such time crystal should return back to its initial state at specific times, while spontaneously locking to an oscillation period that differs from that of any external time-dependent forces. Hence this definition excludes all known classical oscillatory systems such as waves or driven pendulums.
For systems in thermal equilibrium, the existence of time crystals appears to be ruled out. In short, all physically observable properties of quantum systems are time-independent in equilibrium, so no time-periodic behavior can manifest itself. (A more detailed analysis of correlations between different components inside the system also precludes the existence of time crystals in thermal equilibrium [3]). However, a loophole was left open: nonequilibrium systems, such as those that are periodically driven, could still allow time-crystal behavior [4–6]. In this case, if a system were driven with period T, any time crystal would break the discrete time-translational symmetry of the drive and only return to its initial state after discrete multiples of a time nT, where n is an integer [6]. Furthermore, for this discrete time crystal to persist, it must be stabilized against heating to infinite temperature by imposing a phenomenon known as many-body localization, wherein strong random disorder in the system’s potential prevents energy absorption from the drive.
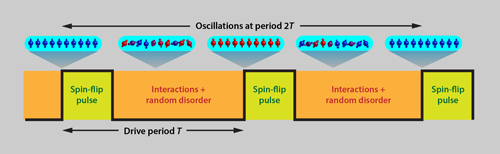
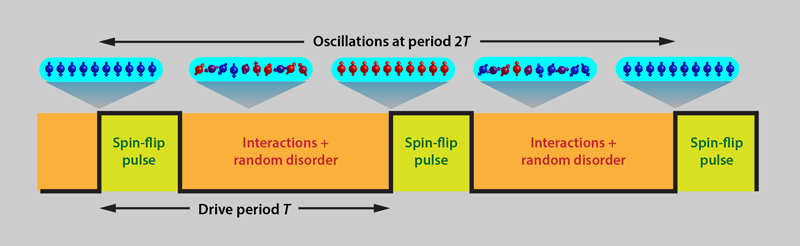
With the stage set, Norman Yao from the University of California, Berkeley, and colleagues [7] studied a theoretical model of a quantum system that would permit such time-crystal behavior. The system, proposed in Ref. [6], is a 1D chain of quantum spins subjected to an alternating drive that first flips all the spins and then allows the spins to interact with each other. The interactions take place in the presence of random, site-dependent external magnetic fields, which support the necessary many-body localization phenomenon (Fig. 1). Within this model, Yao et al. calculated the full range of parameters for which a time crystal should exist and showed how those parameters should change with system size. A crucial property of this time crystal is its “rigidity”: even if the drive parameters are slightly changed (by making the spin-flip pulses imperfect, for instance), the period of the time-crystal oscillations from and to the initial spin state remains rigidly locked. This feature highlights the importance of interactions between the spins, since noninteracting spins would simply follow the imperfect drive.
The authors then proposed a protocol for creating and detecting such a time crystal in a string of cold, trapped ions, emphasizing the time crystal’s rigidity as a distinguishing signature. Moreover, they provided an experimental observable for determining one of the system’s phase boundaries, beyond which it ceases to be a time crystal. Since spin-spin interactions in cold-ion systems decay with a power law in distance, the authors revisited the original model under these conditions, showing that time-crystal behavior should still remain for wide ranges of interaction strengths and spin-flip imperfections. With such a direct theoretical prescription in hand, the challenges of making a time crystal now rested squarely with the experimentalists.
After this proposal was posted on the arXiv in August 2016, experimental observations of a discrete time crystal were achieved by both Chris Monroe’s group at the University of Maryland in September 2016 [8], and by Mikhail Lukin’s group at Harvard University in October 2016 [9]. In Monroe’s work, the quantum spins that created the time crystal were encoded in a string of trapped ytterbium ions and coupled together through their mutual Coulomb interaction. While applying alternating sequences of precisely tuned laser pulses, which could optically drive spin flips or generate spin-spin interactions with random disorder [10], the group monitored the time evolution of each spin’s magnetization. As predicted by Yao et al., the system exhibited emergent oscillations in the spins’ magnetizations that were locked at twice the drive period (Fig. 1). These oscillations persisted even when parameters of the drive were varied, thereby heralding the long-desired time crystal.
Meanwhile, Lukin’s group studied an ensemble of nearly one million dipolar spin impurities in diamond, called nitrogen-vacancy centers. The team employed microwave radiation to alternately flip the spins of the impurities and to generate their spin-spin interactions, all in the presence of random disorder occurring natively within the diamond bulk. Despite using a completely different quantum system to that of Monroe’s group, the researchers observed the same significant features of a time-crystal state: oscillations at integer multiples of the drive period T (both 2T and 3T in this work) and robustness to perturbations in the drive parameters. Furthermore, both groups have performed initial measurements of the location of the time-crystal phase boundary predicted by Yao et al., outside of which the time crystal “melts” into a symmetry-unbroken state. Such similar results achieved in two wildly disparate systems underscore that time crystals are a broad new phase of matter, not simply a curiosity relegated to small or narrowly specific systems.
Symmetry breaking is a pervasive concept in physics, explaining diverse phenomena such as spatial crystals, superconductivity, and the Higgs mechanism. Yet until recently, time-translation symmetry was the “lone holdout” [6], in that there was no known way to break it. Observation of the discrete time crystal in a periodically driven, nonequilibrium quantum system confirms that symmetry breaking can occur in essentially all natural realms, and clears the way to several new avenues of research. Many unknown and unexplored phases of matter are predicted to exist only in such systems, and the experimental tools needed to create them have now been demonstrated for the first time. Although the full practical implications are not yet known, it is expected that such systems can exhibit topological order (the subject of the 2016 Nobel Prize in Physics), which can potentially stabilize quantum states against decoherence effects that limit their useful lifetime. These enhanced quantum states could form the basis of more robust quantum memories or improved devices for precision measurement. Taken together, the work presented by these three groups [7–9] caps an intriguing story of scientific discovery—and it’s about time.
This research is published in Physical Review Letters and posted on the arXiv.
References
- F. Wilczek, “Quantum Time Crystals,” Phys. Rev. Lett. 109, 160401 (2012).
- P. Bruno, “Comment on “Quantum Time Crystals”,” Phys. Rev. Lett. 110, 118901 (2013).
- H. Watanabe and M. Oshikawa, “Absence of Quantum Time Crystals,” Phys. Rev. Lett. 114, 251603 (2015).
- V. Khemani, A. Lazarides, R. Moessner, and S. L. Sondhi, “Phase Structure of Driven Quantum Systems,” Phys. Rev. Lett. 116, 250401 (2016).
- C. W. von Keyserlingk, V. Khemani, and S. L. Sondhi, “Absolute Stability and Spatiotemporal Long-Range Order in Floquet Systems,” Phys. Rev. B 94, 085112 (2016).
- D. V. Else, B. Bauer, and C. Nayak, “Floquet Time Crystals,” Phys. Rev. Lett. 117, 090402 (2016).
- N. Y. Yao, A. C. Potter, I. D. Potirniche, and A. Vishwanath, “Discrete Time Crystals: Rigidity, Criticality, and Realizations,” Phys. Rev. Lett. 118, 030401 (2017).
- J. Zhang et al., “Observation of a Discrete Time Crystal,” arXiv:1609.08684.
- S. Choi et al., “Observation of Discrete Time-Crystalline Order in a Disordered Dipolar Many-Body System,” arXiv:1610.08057.
- J. Smith, A. Lee, P. Richerme, B. Neyenhuis, P. W. Hess, P. Hauke, M. Heyl, D. A. Huse, and C. Monroe, “Many-body Localization in a Quantum Simulator with Programmable Random Disorder,” Nature Phys. 12, 907 (2016).