Physical Model of Skull Growth
The human skull changes shape as it grows, and physicians and biologists would like to understand the causes of these changes and ultimately predict them. Now a team has developed a model that predicts skull shape changes based on physics and geometry principles alone, without any reference to biochemistry or genetics. The model successfully describes the development of known skull deformities and helps explain the ways in which growing bones react to mechanical cues. It also provides a first step toward a model that could guide surgeons treating infants with abnormal skull growth.
The growth of the skull in harmony with the brain is a complex process. Biologists have traditionally focused on biochemistry and genetics as the main drivers of bone growth, but some researchers have felt that the mechanical stresses produced by the growing brain are equally important. How cells detect and react to mechanical signals such as pressure is a fundamental question that has perplexed biologists for at least a century [1, 2].
Mathematician Alain Goriely of Oxford University in the UK and biomechanical engineer Ellen Kuhl of Stanford University in California, along with colleagues, have now developed computational tools to simulate the growth and evolving shape of the cranial vault—the “brain space” within the skull—in a way that is entirely based on mechanical effects. A future version of the model could guide surgeons who must remove parts of the skull to treat infants whose heads are growing improperly. This type of surgery is currently “more an art and craft than science,” says Goriely.
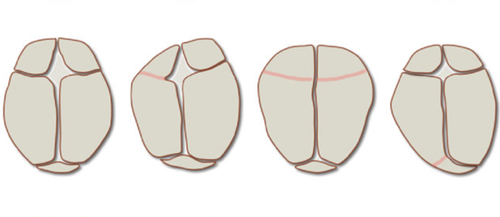
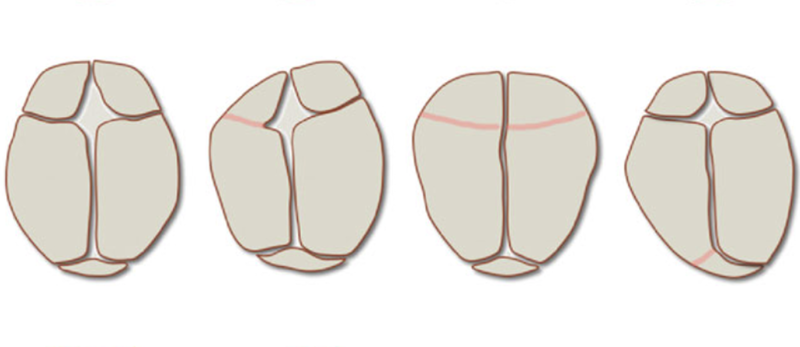
The team incorporated two bone growth processes into their model. Most bone activity in a newborn’s skull occurs along the sutures, soft fibrous boundaries between adjacent bone plates. As new bone accretes on either side of the suture—starting with a layer of specialized, pre-bone cells —the plates push against one another, and the bones grow outward, away from this boundary. The second process, called remodeling, occurs as existing bone is removed from the inner surface of the plates, and new bone accretes on the outer surface. Remodeling allows the skull’s curvature to decrease as it enlarges and also causes an increase in bone thickness.
The researchers started with the simplest case of a skull whose shape remains constant as it grows. Treating the skull as a semi-ellipsoid divided into patches that represented the bones of the cranial vault, they simulated volumetric expansion of the brain, thickness changes of the bones, and area growth along the sutures with so-called finite-element simulations. These simulations relied on estimates of pressures, stresses, and strains, based on bone growth and deposition rates that the team obtained from published sources.
The simulations allowed the researchers to study the deformities that result when the soft tissue between two plates hardens too early, halting growth from the suture. Ceasing growth along suture lines at various time steps allowed the team to observe the evolution of abnormal skull shapes. Without tuning any parameters, the model predicted deformed skull shapes accurately. “These shapes agree strikingly well with the shapes observed in patients for which selected growth plates fuse too early,” says Kuhl.
Goriely, Kuhl, and their colleagues also wanted to identify the most important mechanical signal that triggers bone growth at the level of cells. It could be pressure against the skull’s inner surface or the tension induced between plates. But those two parameters remain nearly the same over time, while the bone growth rate decreases with age. So the team suggests that it may be a third option—the width of the stretched suture relative to its equilibrium width (the suture strain), which decreases at the same rate as bone growth.
Next the team plans to couple their model to biochemical processes and analyze the relationships between mechanical and biological stimuli. Jayaratnam Jayamohan, a pediatric neurosurgeon at Oxford University Hospitals, says the work is important. “It is an area that is not well appreciated in the neuro/craniofacial surgical communities,” he says, “and will certainly add to our knowledge of how these and other conditions may arise and be treated.”
This research is published in Physical Review Letters.
–Rachel Berkowitz
Rachel Berkowitz is a Corresponding Editor for Physics Magazine based in Vancouver, Canada.