Scattering Experiments Tease Out the Strong Force
One of the fundamental challenges in nuclear physics is to predict the properties of subatomic matter from quantum chromodynamics (QCD)—the theory describing the strong force that confines quarks into protons and neutrons, and that binds protons and neutrons together. In other words, can QCD explain why subatomic matter is stable, how it comes into being, evolves, and organizes itself, and what phenomena could emerge from it [1]? Improving our understanding of the strong force will be important, for example, in shedding light on the nucleosynthesis processes that create the elements present in the Universe and in illuminating the mechanisms that fuel stars and drive stellar explosions. Now, Amit Kumar of Saint Mary’s University, Canada [2], and co-workers have shown that the scattering of protons by an isotope of carbon can be a sensitive probe of the strong force. Specifically, they have demonstrated that measurements of the scattering cross section are sensitive tests of strong-force models.
At the low energies relevant for most studies of nuclear structure and nuclear reactions, atomic nuclei can be described in terms of nucleons—neutrons and protons. The strong interactions between nucleons make nuclei extremely complex quantum many-body systems. Presently, the best theoretical approach for tackling this complexity is the so-called chiral effective field theory (EFT) [3, 4]. Chiral EFT, based on the intrinsic chiral symmetries of QCD, is an approximation of QCD that uses effective degrees of freedom such as nucleons, pions, and other hadrons. Using a pertubative approach, it provides a systematic framework to construct the two-, three-, and many-nucleon interactions necessary to solve nuclear many-body problems.
In the last decade, advances in chiral EFT, together with the development of powerful many-body computational methods [5] have dramatically pushed the frontiers of nuclear theory, allowing for the description of nuclei with increasingly larger mass numbers. Recently, Hagen et al. successfully used chiral EFT and advanced many-body methods to calculate the nuclear structure of nickel-78 [6]. The same group is now tackling nuclei near tin-100 [7]. Remarkably, computational progress has been so swift that the many-body calculations themselves are not the primary obstacles for computing nuclear properties in this medium-mass region. Theoretical limitations come instead from existing models of two- and three-nucleon (and many-nucleon) interactions [8]. Three-nucleon forces arise naturally in chiral EFT, mirroring the complicated multiquark interactions from QCD. Since EFT is an effective field theory that approximates QCD, the parameters describing these forces cannot be derived directly from QCD itself. Instead, they can be extracted from combining experiments with theoretical calculations. Constraining such parameters from data, however, is not easy, since many of them are not directly related to specific nuclear processes. The hope is that new types of experiments, guided by advanced theoretical calculations, will help us discern between models for two- and three-nucleon forces. This is the framework within which the new work finds its rationale.
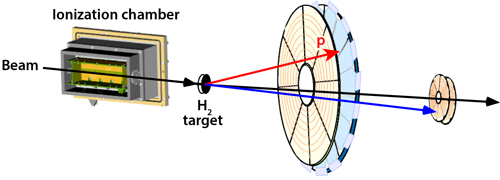
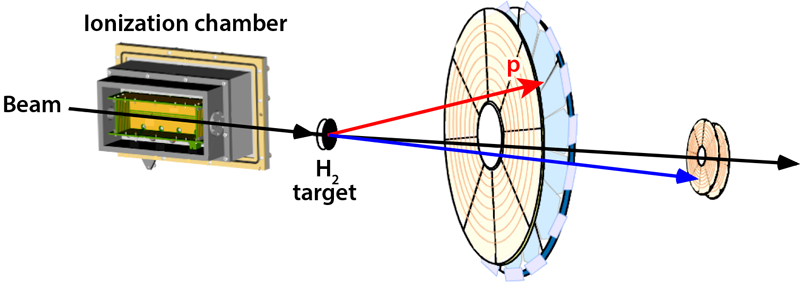
To probe the nuclear force, Kumar and co-workers study the elastic scattering of protons from carbon-10 ( 10C). Rather than hitting a static carbon target with protons, the experiments were carried out in an “inverse kinematics” mode: a beam of 10C isotopes, accelerated by the ISAC rare-isotope beam facility at TRIUMF, Canada’s national laboratory for nuclear and particle physics, bombarded a solid hydrogen target with 10C nuclei at a rate of 2000 particles per second (see Fig. 1). Using position-sensitive detectors, the researchers determined the probability, or cross section, of a proton scattering from a carbon atom at a particular angle. This angular dependence serves as a “fingerprint” for the strong-force interactions within the nuclei.
The use of 10C entails two important advantages. First, it is a nucleus that lies exactly at a nuclear proton dripline—the boundary in the chart of nuclides beyond which nuclei lose stability. Adding one more proton to such a dripline nucleus results in an unstable nucleus that immediately decays radioactively. The neighbors of 10C in the nuclide chart (nitrogen-11, berylium-8, and boron-9) are unstable. Since the nuclear force determines the delicate balance between stability and instability, the sensitivity of nuclear structure to the strong force becomes more pronounced at the dripline. This makes dripline nuclei extremely interesting from both a theoretical and an experimental perspective.
The second advantage of 10C concerns the theoretical description of experiments of protons scattered from it. In a scattering event, one has to consider, in addition to a proton- 10C pair, a virtual intermediate state in which a proton is added to 10C to form nitrogen-11 ( 11N). Because 11N is unbound, only a few of its excited-state levels have to be considered at the energies relevant for the experiment, easing the theoretical analysis. Well-bound nuclei would exhibit a much larger level density, making their reactions more difficult to describe theoretically.
The authors analyze proton scattering from 10C using an ab initio model that accounts for the effects of both bound and unbound states [9]. This approach allows them to precisely describe both a system consisting of a proton separated from 10C and one with all nucleons close together ( 11N). Employing recent parametrizations for the three-nucleon force obtained through chiral EFT, Kumar et al. compared the experimentally determined cross section with theoretical predictions from three existing chiral EFT models for the strong force: one that includes two-nucleon forces only, called the NN model, and two that include different parametrizations of both two- and three-body interactions, called the NN+3N400 and N2LOsat models.
Their analysis showed that the angular distribution of low-energy elastically scattered protons is a sensitive observable for testing strong-force models, in particular for the three-nucleon force. The N2LOsat model (described in Ref. [10]) delivered the best agreement with the angle-dependence data. The reason for its success may lie in the fact that compared to the NN+3N400 model, the N2LOsat model is constructed by fitting the ground-state properties of a larger set of nuclei. The inclusion of more neutron-rich nuclei, in particular, likely gives better constraints for three-nucleon forces than those derived from light nuclei such as deuterium, tritium, helium-3, or helium-4. It is worth noting, however, that all models, including N2LOsat, failed to reproduce the magnitude of the scattering cross section.
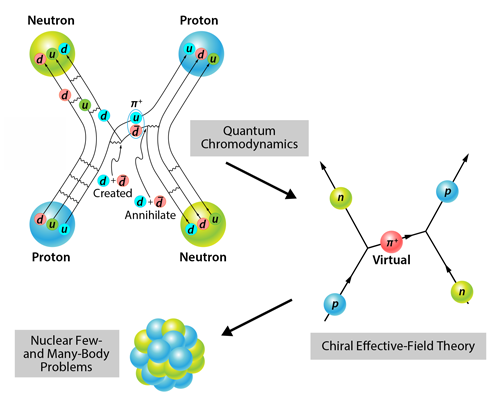
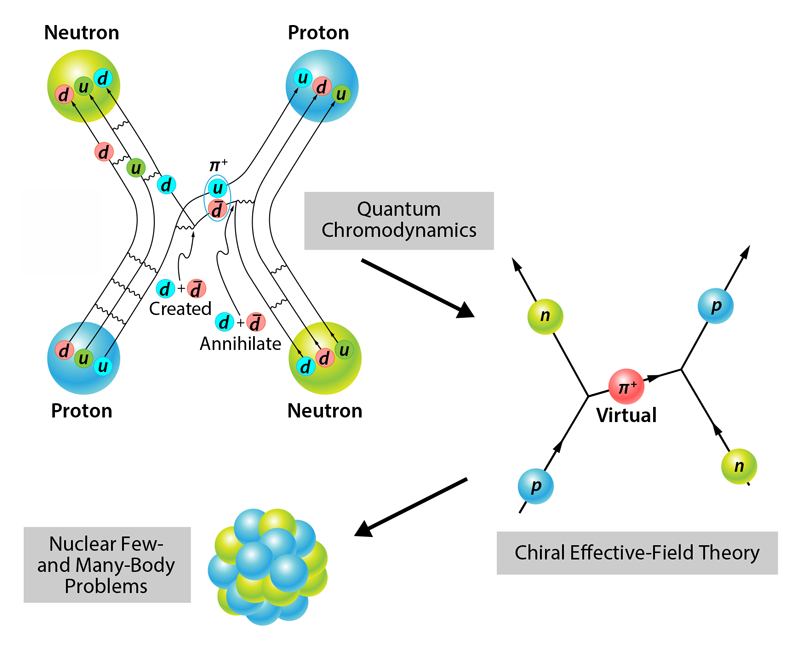
The work of Kumar and colleagues illustrates a paradigmatic approach (see Fig. 2) to achieving a grand goal of nuclear physics: developing a predictive theory that is strongly grounded in QCD. Ideally, we would like to compute properties of nucleonic matter using QCD. Since this problem is too complex, it can be approximated first by using chiral EFT to construct nuclear interactions. Such interactions can in turn be used to solve nuclear few- and many-body problems. The success of such an approach relies on the theory-experiments synergy that is at the very heart of the scientific method. On the theoretical front, QCD approaches like lattice QCD, which formulates the theory on a discrete, as opposed to continuous, spacetime, will need to deliver EFT Hamiltonians that are more directly connected to the underlying theory for the strong force. At the experimental level, approaches like that of Kumar et al. will help researchers identify the most sensitive ways to test theoretical models in the lab.
This research is published in Physical Review Letters.
References
- A. Aprahamian et al., Reaching for the Horizon: The 2015 Long Range Plan For Nuclear Science (2015) http://inspirehep.net/record/1398831.
- A. Kumar et al., “Nuclear Force Imprints Revealed on the Elastic Scattering of Protons With 10C,” Phys.Rev. Lett. 118, 262502 (2017).
- R. Machleidt and D. R. Entem, “Chiral Effective Field Theory and Nuclear Forces,” Phys. Rep. 503, 1 (2011).
- E. Epelbaum, H.-W. Hammer, and Ulf-G. Meißner, “Modern Theory of Nuclear Forces,” Rev. Mod. Phys. 81, 1773 (2009).
- An Advanced Course In Computational Nuclear Physics: Bridging The Scales From Quarks To Neutron Stars, edited by M. Hjorth-Jensen, M. P. Lombardo, and U. van Kolck Lecture Notes in Physics Vol. 936 (Springer, New York, 2017)[Amazon][WorldCat]; See chapters 4–11 for recent progress in EFT and various few- and many-body methods.
- G. Hagen, G. R. Jansen, and T. Papenbrock, “Structure of 78Ni from First-Principles Computations,” Phys. Rev. Lett. 117, , 172501 (2016).
- G. Hagen, private communication.
- B. D. Carlsson, A. Ekström, C. Forssén, D. Fahlin Strömberg, G. R. Jansen, O. Lilja, M. Lindby, B. A. Mattsson, and K. A. Wendt, “Uncertainty Analysis and Order-by-Order Optimization of Chiral Nuclear Interactions,” Phys. Rev. X 6, , 011019 (2016).
- P. Navrátil, S. Quaglioni, G. Hupin, C. Romero-Redondo, and A. Calci, “Unified ab initio Approaches to Nuclear Structure and Reactions,” Phys. Scr. 91, 053002 (2016).
- A. Ekström, G. R. Jansen, K. A. Wendt, G. Hagen, T. Papenbrock, B. D. Carlsson, C. Forssén, M. Hjorth-Jensen, P. Navrátil, and W. Nazarewicz, “Accurate Nuclear Radii and Binding Energies from a Chiral Interaction,” Phys. Rev. C 91, 051301 (2015).