The Thermodynamic Cost of Measuring Time
The ability to precisely measure time has had a dramatic impact on society, from the marine chronometers that facilitated navigation in the 18th century, to the satellite-borne atomic clocks that enable the Global Positioning System (GPS) today. But what fundamental limitations does physics place on our ability to measure time? In a new paper, Paul Erker from the Autonomous University of Barcelona, Spain, and colleagues [1] argue that thermodynamics plays a key role in such limitations. Considering a simple model of a quantum clock, they establish a quantitative connection between two of its features—accuracy and resolution—and the “thermodynamic cost” of running it in terms of its heat dissipation and entropy increase. Thermodynamics also lies at the heart of our perception that time flows inexorably forwards from the past to the future. These results therefore link our ability to measure time with the flow of time itself.
Quantum theory underpins almost all contemporary physics and has been used to design the most accurate clocks existing today. To investigate the fundamental limits of measuring time, Erker and colleagues therefore focused on quantum clocks. To ensure that all aspects were fully accounted for, they considered an autonomous clock, which operates without any external control or power supply, generating a sequence of “ticks” that are transmitted to the outside world. A number of other interesting models of autonomous quantum clocks have been considered (see, for example, Refs. [2–8]), the performance of which do not appear to be influenced by thermodynamics. However, these do not tick in the same sense as Erker and co-workers’ model, and they generally involve either unphysical systems that have no minimum energy or initial states whose preparation would arguably require precise timings provided by an additional clock. A key advantage of Erker and co-workers’ model is that the initial state does not need to be fine-tuned nor does it require any precise timings to prepare. A model of a ticking autonomous clock similar to the one considered here was also presented in a previous paper [9], but an advantage of Erker and colleagues’ model is that it explicitly includes the physical workings and power supply of the clock.
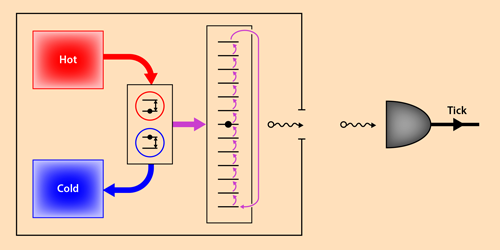
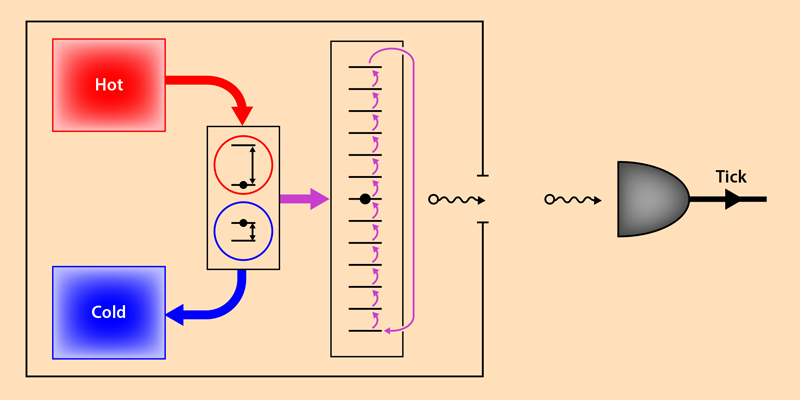
In particular, the new clock is comprised of the smallest possible heat engine [10], consisting of just two quantum systems, each with two energy levels. The engine is connected to two thermal baths, one hot and one cold. In addition, it is connected to a load system, which has a finite “ladder” of possible states with equally spaced energies. As the clock evolves, heat flows from the hot bath to the cold, raising the load up the ladder. When the load reaches the top of the ladder, it rapidly decays to the bottom, emitting a photon into a detector that yields a tick of the clock, and the process begins again (Fig. 1). The performance of the clock is described in terms of its resolution (the frequency of successive ticks) and its accuracy (the number of ticks before the timing of the clock is uncertain by approximately one tick).
Interestingly, the team discovered that the achievable resolution and accuracy of the clock depend on the amount of heat dissipated into the cold bath, with more dissipated heat leading to improved performance. Furthermore, by altering the parameters of the clock, such as the number of steps in the ladder, this improvement in performance can be applied to either the accuracy or the resolution, with a nonlinear trade-off between the two quantities. The heat dissipated in the cold bath is closely related to the entropy increase of the clock, and the authors show that in a particular limit (in which the ladder has many steps and is weakly coupled to the engine), the accuracy of the clock is equal to half of its entropy increase—a surprisingly simple connection between two very different quantities. The increasing entropy of the Universe, as it evolves towards more disordered states, is believed to give rise to the asymmetry we perceive in time. For example, an object dropped on the floor can dissipate its energy as heat, but we do not see the reverse, in which an object is propelled off the floor by absorbing heat. These results therefore provide a quantitative connection between the irreversible flow of time suggested by thermodynamics and our ability to measure it.
The team argues that a similar connection will apply to other autonomous quantum clocks and that an increase in entropy is a necessary component of such models. A key argument is that an autonomous quantum clock operates as a machine with finite power, and this is believed to be impossible without an increase in entropy—essentially any perfectly efficient clock would tick infinitely slowly. Although this is a strong argument, it would be interesting to explore other models of thermodynamical clocks and to understand the general case in more detail, both conceptually and quantitatively.
It would also be good to determine the relationship between thermodynamical quantum clocks and the more mechanical quantum clocks considered previously [2–8] in which entropy does not appear to play a central role. Finally, one could study additional properties of autonomous quantum clocks, such as their sensitivity to the precise initial state or their longevity (the time after which their accuracy and resolution notably decrease). Note that in the latter case, thermodynamics also appears to play a crucial role, as an autonomous clock cannot continue to operate once it has reached a timeless equilibrium state.
This research is published in Physical Review X.
References
- P. Erker, M. T. Mitchison, R. Siva, M. P. Woods, N. Brunner, and M. Huber, “Autonomous Quantum Clocks: Does Thermodynamics Limit our Ability to Measure Time?,” Phys. Rev. X 7, 031022 (2017).
- A. Peres, “Measurement of Time by Quantum Clocks,” Am. J. Phys. 48, 552 (1980).
- D. N. Page and W. K. Wootters, “Evolution without Evolution: Dynamics Described by Stationary Observables,” Phys. Rev. D. 27, 2885 (1983).
- Y. Aharonov and T. Kaufherr, “Quantum Frames of Reference,” Phys. Rev. D 30, 368 (1984).
- V. Bužek, R. Derka, and S. Massar, “Optimal Quantum Clocks,” Phys. Rev. Lett. 82, 2207 (1999).
- J. Lindkvist, C. Sabín, G. Johansson, and I. Fuentes, “Motion and Gravity Effects in the Precision of Quantum Clocks,” Sci. Rep. 5, 10070 (2015).
- A. S. L. Malabarba, A. J. Short, and P. Kammerlander, “Clock-Driven Quantum Thermal Engines,” New J. Phys. 17, 045027 (2015).
- M. Woods, R. Silva, and J. Oppenheim, “Autonomous Quantum Machines and Finite Sized Clocks,” arXiv:1607.04591.
- S. Rankovic, Y.-C. Liang, and R. Renner, “Quantum Clocks and Their Synchronisation—The Alternate Ticks Game,” arXiv:1506.01373.
- N. Brunner, N. Linden, S. Popescu, and P. Skrzypczyk, “Virtual Qubits, Virtual Temperatures, and the Foundations of Thermodynamics,” Phys. Rev. E 85, 051117 (2012).