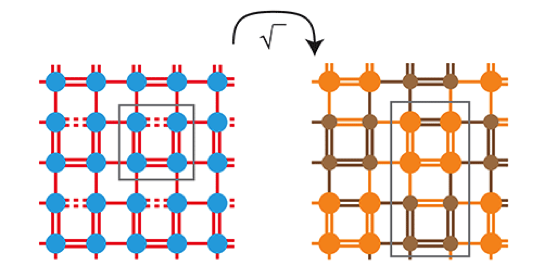
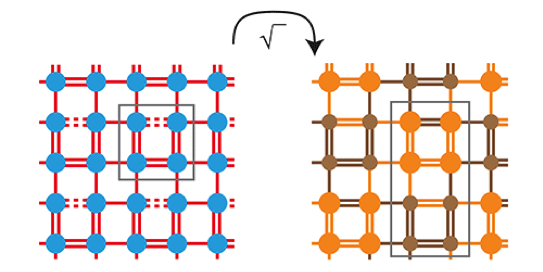
The Square Root to Topological States
How do you design a topological material from scratch? That’s a question researchers are asking a lot these days as they look to build lattices for electrons, atoms, light, and sound that, by virtue of the lattice’s symmetry, host states that are immune to disturbance. Jake Arkinstall of Lancaster University, UK, and colleagues offer one answer: start with a regular crystal lattice and then take the square root of the quantum-mechanical equation that describes it. In certain cases, the solution of this new equation will describe a lattice with topological states. And unlike other recipes for engineering topological materials, this one doesn’t introduce new ingredients—the elements in the “parent” lattice and its square-root “child” are the same, it’s only the couplings between the elements that change.
The team’s approach has a famous precedent: In the 1920s, Dirac discovered the positron when he took the square root of the Klein-Gordon equation for relativistic particles. Arkinstall and colleagues carry this idea over to so-called tight-binding models, which are often used to calculate the energy bands for electrons in solids or light in a waveguide array. First, they consider a representative example: a 1D lattice with topological states known as the bow-tie lattice, which consists of atom pairs placed head-to-toe in a line. They show that the Hamiltonian for this lattice is the square root of the Hamiltonian for a (nontopological) lattice of atom pairs arranged like steps in a ladder. Extrapolating from this case, the authors define general features of a square-root operation that results in a topological lattice, both in 1D and in 2D.
This research is published in Physical Review B.
–Jessica Thomas
Jessica Thomas is the Editor of Physics.