Even Flocks are Topological
Birds in a flock, cells in a colony, and other forms of “active matter” can, much like atomic spins in a solid, be described by a model of collective behavior. A research team has now adapted such a flocking model to describe entities moving on a curved surface—as opposed to on a plane or in free space as earlier treatments of the model have usually assumed. The team’s model might apply to cells roaming the folds of the gut or so-called active colloids moving in curved environments. It also predicts behavior reminiscent of topological insulators, which are being actively explored because of their unusual electronic properties.
Suraj Shankar and colleagues at Syracuse University, New York, used an established approach that describes a flock not as a collection of discrete moving particles but rather as a continuous medium defined by a velocity field. This model assumes that the velocity at any point in the field will align with the average velocity of its immediate surroundings. Above a certain average density, this interaction results in a uniform velocity for the medium, mimicking the in-unison flight of birds.
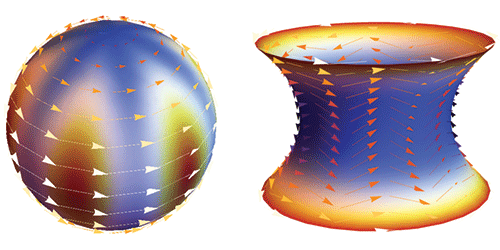
Shankar and his colleagues modified this flocking model to describe objects that are forced to move on the surface of a sphere. With this constraint, the velocity field breaks into bands in which the flocks circulate either east-to-west or west-to-east along the surface. The researchers’ model also predicts, for certain parameters, sound-wave-like excitations that are confined to the equator and travel undeterred by inhomogeneities or small obstacles. This “protection” comes from the surface’s curvature and the breaking of time-reversal symmetry (from the unidirectional motion of the flocks), much as the protection of surface states in topological insulators comes from symmetries in the material.
This research is published in Physical Review X.
–Jessica Thomas
Jessica Thomas is the Editor of Physics.