Record Distance for Quantum Cryptography
Protecting the security of data is a crucial aspect of our networked society. One of the most promising approaches to secure communications is based on cryptographic techniques that exploit the fundamental laws of quantum mechanics. In quantum key distribution (QKD), two communicating parties (Alice and Bob) use photons to share an encryption key with absolute security, as an eavesdropper (Eve) cannot extract information from the photons without being noticed. Progress in QKD technology has been swift in the last decade: QKD systems have been tested by banks and governments and deployed at the 2010 World Cup in South Africa. In 2017, researchers held a QKD-protected video conference between China and Austria using the quantum satellite Micius as a trusted relay [1]. To create a commercially viable alternative to conventional cryptography, research is focusing on making QKD cheaper and more practical as well as working on increasing its range and the transmission rate of the encryption key. Now Alberto Boaron from the University of Geneva and his colleagues report a new distance record (421 km) [2] for optical-fiber-based QKD. While this is a modest distance improvement over the previous record (404 km) [3], the new scheme can exchange an encryption key at much faster rates—an important asset for applications. However, the previous 404-km scheme involved a version of QKD known as measurement-device-independent QKD (MDI-QKD), which offers a higher degree of practical security.
Since the first QKD transmission across 32 cm of an optical bench [4], extending QKD’s range has been a primary research goal. A major obstacle is posed by the fact that most photons are scattered or absorbed before getting to the receiver. In a standard optical fiber, a photon’s chances of survival are 10% after 50 km and fall to only 0.01% after 200 km. This is devastating considering that standard optical repeaters can’t faithfully regenerate a quantum signal, and quantum repeaters are still beyond today’s technological reach. Even so, QKD has been demonstrated over 240 km [5], 307 km [6], and now 421 km [2] of optical fiber [7]. These results were possible thanks to the availability of optical fibers with ultralow losses and QKD systems with high clock rates. Even with large signal loss, the count rate in Bob’s detectors can exceed a thousand counts per second if billions of photons are transmitted every second. Another important factor has been the progress in reducing detector noise. If the level of noise is extremely low, the signal-to-noise ratio (SNR) can be high enough to allow Bob to translate all the counts he detects into secure bits of the final key. Bob just has to wait long enough to harvest a sufficiently long quantum key. Detector noise, however, remains an important limiting factor. The thermally induced detections give rise to false positives called dark counts. Since the signal decays exponentially fast with distance, whereas detectors’ dark counts stay constant, at a certain distance the SNR becomes too small, and the QKD system’s encryption-key transmission rate, or key rate, falls to zero.
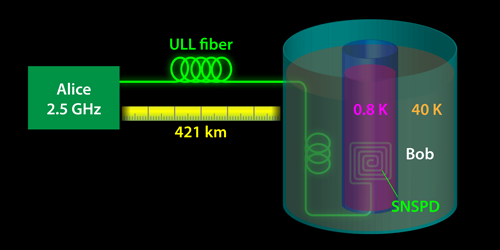
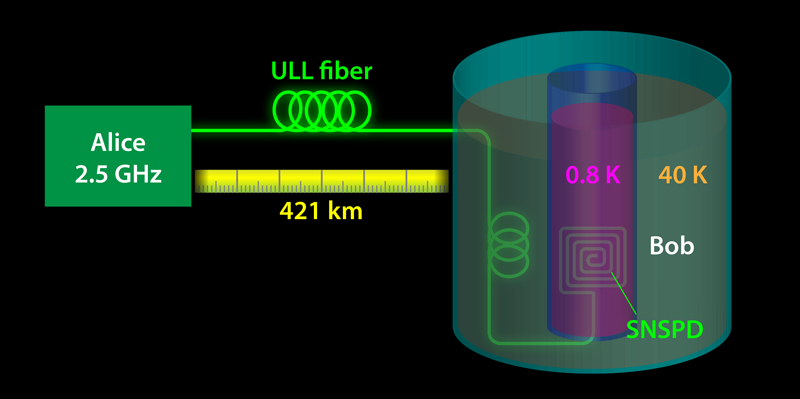
Targeting detector noise was the key ingredient behind the success of Boaron and co-workers. The pulses sent by Alice at a wavelength of 1550 nm propagated through hundreds of kilometers of fiber and were detected by Bob using in-house-made superconducting nanowire single-photon detectors (SNSPDs) (Fig. 1). Each one of these sensitive devices is made of a long, superconducting nanowire that is arranged in a spiraling pattern on a flat surface. To reduce the dark counts in the detectors, the team cooled them down to 0.8 K and used a fiber filter cooled to 40 K to cut off the black body emission of the optical fiber connected to the detectors. These measures reduced the dark count rate to an impressive 0.1 Hz, about 2 orders of magnitude lower than commercially available SNSPDs. With these technical tricks, the probability of detecting a dark count when a photon was expected was lowered to 10−11.
Thanks to the low number of dark counts at the detectors and to the use of an ultralow-loss fiber, combined with a modification of a loss-tolerant protocol [8], the team achieved the best long-distance performance to date for fiber-optic QKD. For lengths of fibers ranging from 251 to 404 km, the scheme achieved key rates that were over 100 times higher than previous demonstrations over the same distances, and they remained positive up to a record distance of 421 km. The increase in the key rate was provided by a QKD setup developed recently by the same authors, featuring one of the highest repetition rates (2.5 GHz) ever used in QKD experiments. The researchers also proved the system’s stability by running it for more than 24 hours.
To assess the results of Boaron et al. and the prospect of future improvements, it is useful to compare the new distance record with the previous one [3] based on MDI-QKD, a technique developed to overcome all the potential security loopholes of QKD receivers. MDI-QKD involves a third party called Charlie, who measures the photons sent by Alice and Bob midway along the communication channel and publicly reveals the outcome of his measurements. Even if Charlie can’t be trusted, he cannot steal Alice and Bob’s secret key. One can show that the presence of an intermediate measuring station in MDI-QKD dramatically reduces the noise level due to dark counts. This led me to claim during a 2015 conference in Tokyo that MDI-QKD could reach longer distances than conventional QKD. The 404-km MDI-QKD experiment performed in 2016 [3] seemed to support my claim. But now the work by Boaron and his colleagues challenges it again. So which of the two protocols holds more potential for long distance? Assuming identical conditions for the fiber (the ultralow-loss type), a detailed analysis [9] shows that it’s an extremely close race. The theory of MDI-QKD suggests that, in principle, it has an edge in terms of SNR, but the complex setup required in practice can spoil this advantage. Conventional QKD, which relies on a simpler implementation, can feature higher clock rates and better detection efficiencies.
It is important to stress that the comparison between QKD and MDI-QKD should include a full analysis of security aspects. MDI-QKD provides a stronger security guarantee than QKD, in particular against attacks targeting Bob’s detectors [10] and other components like the beam splitter used by Boaron et al. for the passive basis selection [11]. What’s more, the authors’ security analysis is limited to “collective” attacks, which are not the most general types of attacks [3, 5]. A possible way to further extend the distance while keeping the same security guarantee as MDI-QKD may be offered by the newly proposed “twin-field” QKD [12], which encompasses the best features of QKD and MDI-QKD without significantly increasing the complexity of the setup.
Ultimately, the specific application will dictate which protocol will satisfy particular needs in terms of security, distance, and key rate. The recent long-distance results provide compelling options that potential users can vet for applications like digital telephony in metropolitan networks.
This research is published in Physical Review Letters.
References
- S.-K. Liao et al., “Satellite-relayed intercontinental quantum network,” Phys. Rev. Lett. 120, 030501 (2018).
- A. Boaron et al., “Secure quantum key distribution over 421 km of optical fiber,” Phys. Rev. Lett. 121, 190502 (2018).
- H.-L. Yin et al., “Measurement-device-independent quantum key distribution over a 404 km optical fiber,” Phys. Rev. Lett. 117, 190501 (2016).
- C. H. Bennett, F. Bessette, G. Brassard, L. Salvail, and J. Smolin, “Experimental quantum cryptography,” J. Cryptol. 5, 3 (1992).
- B. Fröhlich, M. Lucamarini, J. F. Dynes, L. C. Comandar, W. W.-S. Tam, A. Plews, A. W. Sharpe, Z. Yuan, and A. J. Shields, “Long-distance quantum key distribution secure against coherent attacks,” Optica 4, 163 (2017).
- B. Korzh, C. C. W. Lim, R. Houlmann, N. Gisin, M. J. Li, D. Nolan, B. Sanguinetti, R. Thew, and H. Zbinden, “Provably secure and practical quantum key distribution over 307 km of optical fibre,” Nat. Photon. 9, 163 (2015).
- For a proper comparison, it is worth mentioning that these studies employed different types of optical fibers with different attenuation coefficients 𝛼: standard, 𝛼=0.2 dB/km; low-loss, 𝛼=0.18 dB/km; and ultralow-loss, 𝛼=0.16 dB/km. When normalizing such distances to standard fibers, the corresponding distances of the above-mentioned experiments would be 216 km [5], 245.6 km [6], and 336.8 km [2].
- K. Tamaki, M. Curty, G. Kato, H.-K. Lo, and K. Azuma, “Loss-tolerant quantum cryptography with imperfect sources,” Phys. Rev. A 90, 052314 (2014).
- In QKD, the SNR scales linearly with the probability that a photon reaches the end of the fiber, while in MDI-QKD it scales with the square root of the same probability, thanks to the detection midway along the fiber link. This suggests that MDI-QKD should have better SNR than QKD at long distances. However, when we plug in the actual experimental parameters for a distance of 404 km, we find a SNR of 20,000 for the QKD setup of Ref. [2] and 2800 for the MDI-QKD setup of Ref. [3]. This advantage corresponds to an additional 53 km of ultralow-loss (ULL) fiber that can be added to the link, explaining the new distance record. This also shows that Boaron et al.’s setup could, in principle, reach 457 km of ULL fiber, but the authors decided to limit the acquisition time to 24 hours while delivering key rates larger than 1 kHz up to 250 km.
- V. Makarov, A. Anisimov, and J. Skaar, “Effects of detector efficiency mismatch on security of quantum cryptosystems,” Phys. Rev. A 74, 022313 (2006).
- H.-W. Li et al., “Attacking a practical quantum-key-distribution system with wavelength-dependent beam-splitter and multiwavelength sources,” Phys. Rev. A 84, 062308 (2011).
- M. Lucamarini, Z. L. Yuan, J. F. Dynes, and A. J. Shields, “Overcoming the rate–distance limit of quantum key distribution without quantum repeaters,” Nature 557, 400 (2018).