Dissecting the Mass of the Proton

André Walker-Loud

Viewpoint

Dissecting the Mass of the Proton

Nuclear Science Division, Lawrence Berkeley National Laboratory, Berkeley, CA, USA

November 19, 2018• Physics 11, 118

A calculation determines four distinct contributions to the proton mass, more than 90% of which arises entirely from the dynamics of quarks and gluons.

Figure caption — **Figure 1:** The proton is comprised of two up quarks and one down quark, but the sum of these quark masses is a mere 1% of the proton mass. Using lattice QCD, Yang and colleagues determined the relative contributions of the four sources of the proton mass [1]. (The cumulative contributions in MeV/c² are shown on the dark green rectangles.)

Nearly all the mass of known matter is contained within protons and neutrons—the particles that make up the nuclei of atoms. But how do the protons and neutrons acquire their mass? Each of these particles, or “nucleons,” is composed of a dense, frothing mess of other particles: quarks, which have mass, and gluons, which do not. Yet the quark masses only add up to a mere 1% of a proton or neutron’s mass, with the bulk of the proton mass coming purely from the motion and confinement of quarks and gluons. Yi-Bo Yang of Michigan State University, East Lansing, and colleagues have now quantified, for the first time, four separate contributions to the proton’s mass with a calculation based on quantum chromodynamics (QCD), the fundamental theory of the strong interaction in the nucleus and a cornerstone of the standard model of particle physics [1]. While this four-part decomposition has been known for more than 20 years [2], physicists' understanding of it has been only qualitative.

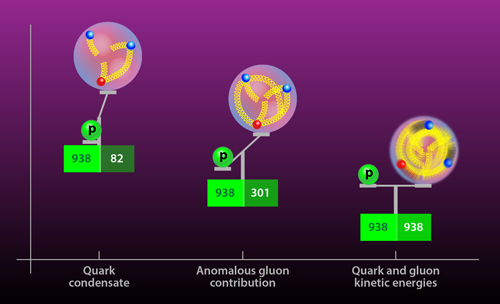
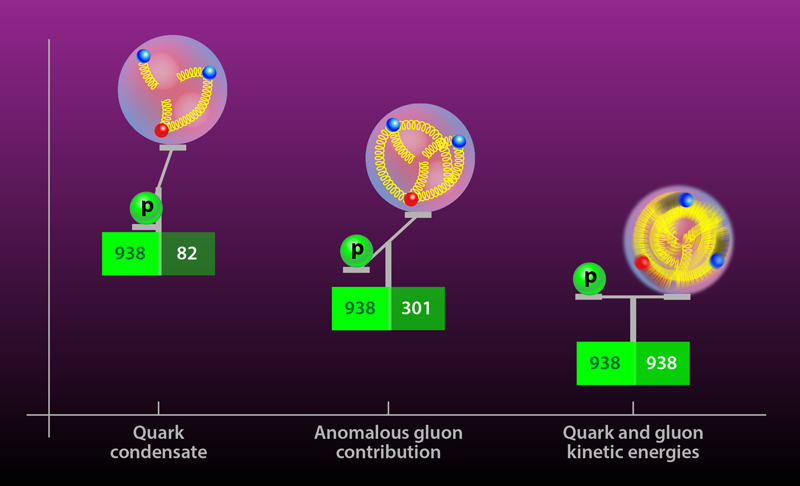
The quarks that make up the proton and neutron are fundamental particles, which get their masses through the Higgs mechanism. The same mechanism doesn’t explain the mass of the proton, which is comprised of two up quarks ( $2.4 MeV ∕ c^{2}$ each) and one down quark ( $5.0 MeV ∕ c^{2}$ ) [3]. Clearly, the sum of these three masses falls far short of the actual proton mass, $938.27 MeV ∕ c^{2}$ . Now, quantum mechanics tells us there is also mass (or equivalently, energy) associated with the confinement of the quarks into the proton, whose diameter is about $1 0^{- 15} m$ . Using an uncertainty principle argument, the confined position of the particles translates into a large momentum and should add about $300 MeV ∕ c^{2}$ —in the right ball park of the proton mass but still too small. (Similar arguments apply to the neutron, which is comprised of two down quarks and an up quark.)

In fact, accurate standard model predictions of both the proton and neutron mass have existed for a decade [4]. At the low energies relevant to a nucleus, these masses can be predicted from just three parameters: an overall mass scale, which is dynamically generated in QCD, and the up and down quark parameters. The proton and neutron masses are known much more precisely from experiment than will ever be possible from standard model predictions. However, physicists would like to understand how the masses emerge from QCD, much the same way they can predict the spectrum of hydrogen from quantum theory.

Yang and colleagues have done just this, determining for the first time the various contributions to the proton mass that arise from quark and gluon dynamics [1]. The researchers rely on a powerful method known as lattice QCD, which places quarks on the sites of a lattice and gluons on the links between them. This rigorous representation of QCD can be implemented numerically, and it is the only QCD-based method that can make quantitative predictions on length scales comparable to the proton or larger. (At these scales, the interactions between quarks and gluons are so strong, they cannot be handled with Feynman diagrams and other “perturbative” methods.) However, lattice QCD is an expensive technique. The discretization creates errors, and to remove them entails taking the lattice spacing, a, to zero. This step is achieved in practice by performing multiple calculations at different values of a, at a high numerical cost that scales as a^-6. Nevertheless, lattice QCD has matured significantly in recent years, allowing for the most precise determination of the quark masses [5] and many properties of light and heavy mesons [3], which are comprised of a quark and an antiquark.

A three-quark particle like the nucleon is exponentially more complicated for lattice QCD, and successful calculations, with all sources of uncertainty controlled, have been rare. In their work, Yang and collaborators overcome some of the complications by using new computational methods that they, along with others, developed [6–8]. These advances enabled them to compute the contribution to the proton mass from four sources [2] known as the quark condensate ( $\sim$ 9%), the quark energy ( $\sim$ 32%), the gluonic field strength energy ( $\sim$ 37%), and the anomalous gluonic contribution ( $\sim$ 23%) (Fig. 1). The smallest contribution, the quark condensate, is a mixture of the up and down quarks and a “sea” of virtual strange quarks, and it is the only one that would vanish if the quark masses were zero. The other three terms are all related to the dynamics of the quarks and gluons and their confinement within the proton. The quark energy and gluonic field strength equate to the kinetic energy of the confined quarks and confined gluons, respectively. The anomalous term is a purely quantum effect. It is associated with the QCD mass scale and consists of contributions from condensates of all quark flavors, including the strange, charm, bottom, and top quarks. The calculation by Yang and colleagues shows that, if the up, down, and strange quark masses were all zero, the proton would still have more than 90% of its experimental mass. In other words, nearly all the known mass in the Universe comes from the dynamics of quarks and gluons.

Physicists have long wanted to understand the emergence of the nucleon mass in terms of the standard model, and the findings from Yang and co-workers are an important contribution to that goal. Their work and other works like it also signify a new era, in which our understanding of nucleons is increasingly shaped by quantitative predictions based on lattice QCD. Just this year, researchers used lattice QCD to determine the nucleon axial charge, a ubiquitous quantity in nuclear physics, with an unprecedented 1% precision [9]. Lattice QCD, coupled with powerful analytic methods for simplifying QCD calculations, will lead to a better understanding of the substructure of the nucleon [10], which is being explored at various colliders around the world and would be one focus of a proposed machine called the Electron-Ion Collider. Ultimately, the hope is that lattice QCD can be applied to a nucleus (multiple nucleons). Nuclei are used as detectors in several experimental searches for beyond-standard-model physics, such as dark matter, a permanent electric dipole moment, and neutrinoless double-beta decay. Interpreting these experiments will require a quantitative understanding of nuclear physics that is rooted in the standard model. This sort of complex problem is increasingly in the realm of lattice QCD thanks to the availability of the near-exascale computers, Sierra and Summit, which are coming online now and are 10 to 15 times more powerful than even those used by Yang and co-workers.

This research is published in Physical Review Letters.

References

Y.-B. Yang, J. Liang, Y.-J. Bi, Y. Chen, T. Draper, K.-F. Liu, and Z. Liu, “Proton mass decomposition from the QCD energy momentum tensor,” Phys. Rev. Lett. 121, 212001 (2018).
X.-D. Ji, “QCD analysis of the mass structure of the nucleon,” Phys. Rev. Lett. 74, 1071 (1995).
S. Aoki et al., “Review of lattice results concerning low-energy particle physics,” Eur. Phys. J. C 77, 112 (2017); Quarks do not have a mass in the sense that the electron does. But a mass parameter for the quarks can still be rigorously defined with a specified renormalization scheme and scale. The masses quoted by Aoki et al. are in the so-called MS-bar scheme at a scale of 2 GeV.
S. Durr et al., “Ab initio determination of light hadron masses,” Science 322, 1224 (2008).
A. Bazavov et al., “Up-, down-, strange-, charm-, and bottom-quark masses from four-flavor lattice QCD,” Phys. Rev. D 98, 054517 (2018).
K-F. Liu, J. Liang, and Y.-B, Yang, “Variance reduction and cluster decomposition,” Phys. Rev. D 97, 034507 (2018).
Y.-B. Yang, M. Gong, J. Liang, H.-W. Lin, K.-F. Liu, D. Pefkou, and P. Shanahan, “Nonperturbatively renormalized glue momentum fraction at the physical pion mass from lattice QCD,” Phys. Rev. D 98, 074506 (2018).
Y.-B. Yang, R. Sufian, A. Alexandru, T. Draper, M.J. Glatzmaier, K.-F. Liu, and Y. Zhao, “Glue spin and helicity in the proton from lattice QCD,” Phys. Rev. Lett. 118, 102001 (2017).
C. C. Chang et al., “A per-cent-level determination of the nucleon axial coupling from quantum chromodynamics,” Nature 558, 91 (2018).
H.-W. Lin et al., “Parton distributions and lattice QCD calculations: A community white paper,” Prog. Part. Nucl. Phys. 100, 107 (2018).

About the Author

André Walker-Loud is a Staff Scientist at Lawrence Berkeley National Laboratory (LBNL). He received his Ph.D. from the University of Washington, Seattle. He then held postdoctoral research positions at the University of Maryland, The College of William & Mary (W&M), and LBNL followed by a joint appointment as an Assistant Professor of Physics at W&M and as a Senior Staff Scientist at Thomas Jefferson National Accelerator Facility. In his research, he uses lattice QCD and effective field theory to gain a quantitative understanding of how nuclear physics emerges from QCD. He is also interested in probing the limits of the standard model by testing fundamental symmetries in nuclear environments.