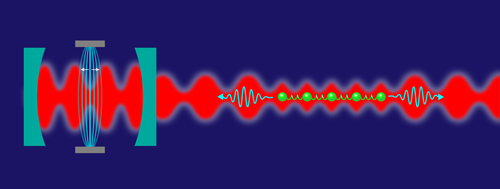
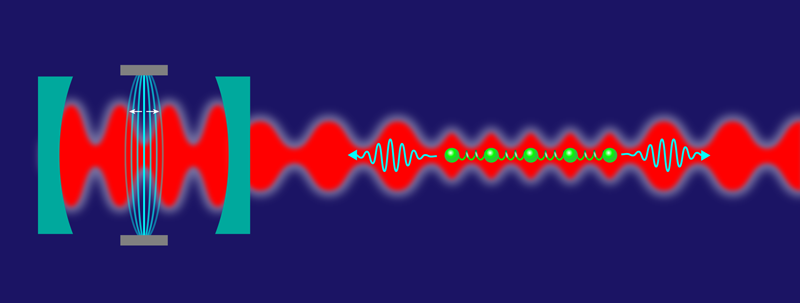
Atoms Oscillate Collectively in Large Optical Lattice
Optical lattices are key elements in the effort to use ultracold atoms for quantum simulation, quantum computing, and atomic clocks. These lattices rely on light forces to precisely hold atoms in space and to individually control their internal states [1]. Researchers strive for nearly perfect periodic lattice structures using state-of-the-art laser systems, but the atoms can interfere with these efforts by scattering photons that perturb the light fields that form the lattice. Normally, this backaction is kept at a minimum, but researchers have realized they can harness the atoms’ influence on the lattice for something useful: to generate interactions between atoms. To explore this possibility, Philipp Treutlein from the University of Basel in Switzerland and colleagues have built a hybrid system composed of a one-dimensional optical lattice coupled to vibrations of a mobile membrane inside an optical resonator [2]. The combination of membrane and resonator amplifies the collective motions of the atoms, producing an instability in the membrane vibrations. This instability, which would be undesirable in most situations, is evidence of long-range (phonon-like) interactions between the atoms. Such interactions could be implemented in cold-atom quantum simulations, where they would mimic the phonon dynamics of “real” lattices inside solids.
An optical lattice is essentially a standing-wave pattern generated by two counterpropagating laser beams. The frequency of the beams is tuned below an atomic resonance so that the atoms are attracted to intensity maxima (antinodes) of the field. It is inevitable that some fraction of the laser photons are scattered by the atoms back into the path of the laser beams. While this backaction is often very small, it can have a significant effect on the trapping fields of the lattice in two possible ways [3, 4]. On the one hand, the collective scattering by atoms within the lattice induces the formation of an optical band gap at the lattice wavelength, which, at first sight, should hamper lattice stability [3]. However, one finds that the lattice adapts its wavelength to cancel this band-gap effect [5]. On the other hand, the stimulated photon redistribution provides for the natural appearance of optomechanical coupling in the form of phonons that cause the atoms to oscillate around their equilibrium positions. Optical lattices are open systems, so the energy that goes into phonons can leak out as heat or can drive strong oscillations that lead to a dynamic instability. Simulations of large lattices have predicted that the optomechanical coupling of atoms will lead to dynamic instabilities, but these models assumed atom numbers that were well above the number that current experiments can accommodate. Still, it has been shown theoretically that instabilities can occur for smaller samples subjected to an asymmetric lattice laser configuration [4].
In their experiment [2], Treutlein and co-workers achieve such an asymmetric configuration with a conceptually simple setup that utilizes a thin elastic membrane inside a high-Q (small bandwidth) optical resonator (see Fig. 1). The researchers direct laser light into the membrane cavity and use the back-reflected light to create a dynamic standing-wave optical lattice potential for a large, cold cloud of roughly rubidium atoms. The optical resonator enhances the membrane vibrations and converts them to phase modulations of the reflected light, which induces collective oscillations of the atomic lattice potential in position and depth. The center-of-mass motion of the membrane thus becomes directly coupled to the phononic atomic modes.
The atoms here experience a dynamic asymmetric lattice potential with the membrane mimicking a much larger extension of the lattice. In this way, the authors reach effective lattice sizes beyond the stability limit. They confirm collective hybrid atom-membrane coupling through the appearance of enhanced lattice excitations (or “antidamping”) despite the presence of extra cooling. In addition, they identify the emergence of the instability by recording high-amplitude vibrations in the membrane, and they find a good fit between their measurements and a model that treats the atoms like a combination of beam splitters [3, 4]. It is important to note that the modeling matches the data only when it includes collective lattice oscillations beyond the center-of-mass dynamics, which is evidence of phonons.
In their experiment, the authors have undoubtedly proven the existence and importance of intrinsic optomechanical couplings and even instabilities in large optical lattices. The risk of instabilities might limit the size of optical lattices for quantum information applications. But the ability to add long-range couplings and phononic degrees of freedom to cold-atom lattices could prove useful for fast, efficient energy transfer, which is needed for sympathetic cooling of macroscopic objects. If this could be done at several laser frequencies, researchers might be able to tailor the range and strength of the atom interactions, opening a new route to fully connected quantum simulators [6]. In the future, not just interactions, but the whole lattice itself could emerge (or “crystallize”) by driving a corresponding instability in a large Bose-Einstein condensate [7–9]. While this sounds a bit like science fiction, a recent experiment recorded the first indications of such spontaneous crystallization [10].
This research is published in Physical Review Letters.
References
- I. Bloch, J. Dalibard, and W. Zwerger, “Many-Body Physics with Ultracold Gases,” Rev. Mod. Phys. 80, 885 (2008).
- A. Vochezer, T. Kampschulte, K. Hammerer, and P. Treutlein, “Light-Mediated Collective Atomic Motion in an Optical Lattice Coupled to a Membrane,” Phys. Rev. Lett. 120, 073602 (201708).
- I. H. Deutsch, R. J. C. Spreeuw, S. L. Rolston, and W. D. Phillips, “Photonic Band Gaps in Optical Lattices,” Phys. Rev. A 52, 1394 (1995).
- J. K. Asbóth, H. Ritsch, and P. Domokos, “Collective Excitations and Instability of an Optical Lattice due to Unbalanced Pumping,” Phys. Rev. Lett. 98, 203008 (2007).
- J. K. Asbóth, H. Ritsch, and P. Domokos, “Optomechanical Coupling in a One-Dimensional Optical Lattice,” Phys. Rev. A 77, 063424 (2008).
- S. Ostermann, M. Sonnleitner, and H. Ritsch, “Scattering Approach to Two-Colour Light Forces and Self-Ordering of Polarizable Particles,” New J. Phys. 16, 043017 (2014).
- D. H. J. O’Dell, S. Giovanazzi, and G. Kurizki, “Rotons in Gaseous Bose-Einstein Condensates Irradiated by a Laser,” Phys. Rev. Lett. 90, 110402 (2003).
- T. Grießer and H. Ritsch, “Light-Induced Crystallization of Cold Atoms in a 1D Optical Trap,” Phys. Rev. Lett. 111, 055702 (2013).
- S. Ostermann, F. Piazza, and H. Ritsch, “Spontaneous Crystallization of Light and Ultracold Atoms,” Phys. Rev. X 6, 021026 (2016).
- I. Dimitrova, W. Lunden, J. Amato-Grill, N. Jepsen, Y. Yu, M. Messer, T. Rigaldo, G. Puentes, D. Weld, and W. Ketterle, “Observation of New Superradiant Regimes in a Bose-Einstein Condensate,” arXiv:1709.02028.