Single Microwave Photons Spotted on the Rebound
Single optical photon detectors typically absorb an incoming photon and use that energy to generate an electrical signal, or “click,” that indicates the arrival of a single quantum of light. Such a high-precision measurement—at the quantum limit of detection—is a remarkable achievement, but the price of that click is in some cases too high, as the measurement completely destroys the photon. If the photon could be saved, then it could be measured by other detectors or entangled with other photons. Fortunately, there is a way to detect single photons without destroying them. This quantum nondemolition photon detection was recently demonstrated in the optical domain [1], and now the feat has been repeated for microwaves. Two research groups—one based at the Swiss Federal Institute of Technology (ETH) in Zurich and the other at the University of Tokyo in Japan—have utilized a cavity-qubit combination to detect a single microwave photon through its reflection off the cavity [2, 3]. The ability to measure microwaves like this without destroying them could help in generating entanglement between distant qubits as well as provide a route toward all-photon-based quantum computation.
The reliable detection of a single microwave photon has been an outstanding goal in microwave quantum optics for the past decade. The challenge is greater than in the optical regime, since a single microwave photon carries 5 orders of magnitude less energy than an optical photon. While researchers have developed techniques to measure single photons stored in a highly confining cavity [4, 5], there is particular interest in the detection of propagating microwave photons. A few single microwave photon detectors have been demonstrated in the last few years [6–8], yet these detectors all resulted in the destruction of the detected photon.
To achieve a quantum nondemolition (QND) measurement of single microwave photons, the research groups in Zurich and Tokyo utilized an approach known as indirect measurement, which contrasts with more direct methods of absorbing the incoming photon. In the indirect approach, the photon interacts with another quantum system, which is often referred to as the pointer. This interaction leads to entanglement between the pointer and the photon, and then at some later time, the pointer can be measured, which collapses the entanglement between the photon and pointer. The advantage of this approach is that the only effect, or “backaction,” on the photon that results from the measurement of the pointer is due to the entanglement between the two quantum systems.
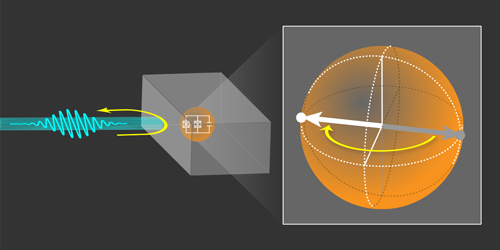
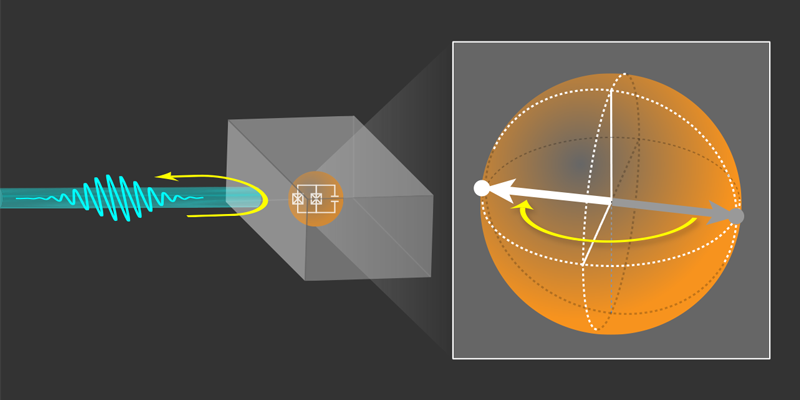
In their experiments, both groups chose as their pointer a transmon circuit—a type of superconducting qubit formed from a Josephson junction shunted by a capacitor. Both groups also placed their transmon in a cavity to mediate the entangling interaction between the incoming photon and the transmon (Fig. 1). The cavity reflects microwave photons, but the details of that reflection—specifically the phase of the reflected photon—depend on the state of the transmon. The transmon is initially placed in a superposition of two states, which can be represented by an arrow in a spherical phase space called the Bloch sphere. The reflection of a single photon off the cavity induces a 180° phase shift in the transmon, which flips the state arrow. Such a flip in the pointer state can be read out separately by sending a secondary probe pulse to the transmon and looking for a specific interference signature.
Despite the conceptual similarities, the two experiments have some important differences that make them complementary. Jean-Claude Besse and co-workers at ETH Zurich [2] characterized their system using a single-photon source. They used separate cavities for entangling the photon and pointer and for reading out the pointer state, which has the advantage of reducing crosstalk between the different fields. By contrast, Shingo Kono from the University of Tokyo and colleagues [3] employed one cavity for both the interaction and measurement. The team also reconstructed the state of the photon after measurement by illustrating how the detection projects the photon field onto a single-photon Fock state, which is a state of exactly one photon. This projection is precisely the minimal backaction that would be expected from a QND detector. For their part, Besse et al. verified the nondemolition aspect of their measurement by showing that the detector did not change the amount of reflected power but randomized the phase of the initial photon state as expected.
Both teams demonstrate detection efficiencies well above 50%, which is already an impressive achievement for these first-generation devices. But the nature of QND opens the possibility of repeatedly measuring the same photon with additional transmon-cavity detectors, thereby providing a route toward improving the detection efficiency even further. The devices do, however, leave substantial room for improvement: the demonstrated single-photon detection is limited to a fairly narrow frequency range near the cavity resonance, as was also the case for the optical QND detector [1]. Researchers would prefer detectors that offer more flexibility in their frequency acceptance.
Perhaps the most exciting application of single-photon detectors in the microwave domain is the way that they can be used to remotely entangle two distant qubits. Reliable and robust remote entanglement will be an essential part of scaling-up quantum computers. Previous work has managed to entangle distant qubits by communicating via continuous microwave signals that are measured with linear detectors [9, 10], but because the signals can be corrupted by unavoidable attenuation, the fidelity of the entangled qubit state was limited. Single-photon detection is less affected by attenuation, as photon loss only reduces the success rate of the entangling operation. The single photons that do arrive at the distant detector are able to entangle the qubits with high fidelity. This type of entangling scheme has recently been demonstrated with the absorbing type of single-photon detector [8], but one drawback is that these direct detectors are limited in efficiency because of the required temporal-mode matching with the photons. The QND detectors demonstrated by the Zurich and Tokyo groups are not limited in this way, so they should exhibit higher efficiency and a greater success rate for the remote entanglement.
Taking advantage of the QND nature of the detection, these single-photon detectors also open the door to quantum computing that only uses microwave photons. Compared to hybrid quantum computer designs that combine light with some other qubit platform, all-photon-based quantum computing has the advantage that photons can exhibit very weak decoherence and offer a natural link between quantum communication and quantum computation [11]. The QND single-photon detectors provide a method to mediate photon-photon interactions by reflecting two photons off the cavity. The resulting photon entanglement is a crucial ingredient in photon-based quantum computing, making microwave photonic quantum computing an exciting possibility in the future.
This research is published in Physical Review X and Nature Physics.
References
- A. Reiserer, S. Ritter, and G. Rempe, “Nondestructive Detection of an Optical Photon,” Science 342, 1349 (2013).
- J.-C. Besse, S. Gasparinetti, M. C. Collodo, T. Walter, P. Kurpiers, M. Pechal, C. Eichler, and A. Wallraff, “Single-Shot Quantum Nondemolition Detection of Individual Itinerant Microwave Photons,” Phys. Rev. X 8, 021003 (2018).
- S. Kono, K. Koshino, Y. Tabuchi, A. Noguchi, and Y. Nakamura, “Quantum Non-Demolition Detection of an Itinerant Microwave Photon,” Nat. Phys. 446, 297 (2018).
- S. Gleyzes, S. Kuhr, C. Guerlin, J. Bernu, S. Deléglise, U. Busk Hoff, M. Brune, J.-M. Raimond, and S. Haroche, “Quantum Jumps of Light Recording the Birth and Death of a Photon in a Cavity,” Nature 446, 297 (2007).
- B. R. Johnson et al., “Quantum Non-Demolition Detection of Single Microwave Photons in a Circuit,” Nat. Phys, 6, 663 (2010).
- Y.-F. Chen, D. Hover, S. Sendelbach, L. Maurer, S. T. Merkel, E. J. Pritchett, F. K. Wilhelm, and R. McDermott, “Microwave Photon Counter Based on Josephson Junctions,” Phys. Rev. Lett. 107, 217401 (2011).
- K. Inomata, Z. Lin, K. Koshino, W. D. Oliver, J.-S. Tsai, T. Yamamoto, and Y. Nakamura, “Single Microwave-Photon Detector Using an Artificial Λ-Type Three-Level System,” Nat. Commun. 7, 12303 (2016).
- A. Narla et al., “Robust Concurrent Remote Entanglement Between Two Superconducting Qubits,” Phys. Rev. X 6, 031036 (2016).
- D. Ristè, M. Dukalski, C. A. Watson, G. de Lange, M. J. Tiggelman, Ya. M. Blanter, K. W. Lehnert, R. N. Schouten, and L. DiCarlo, “Deterministic Entanglement of Superconducting Qubits by Parity Measurement and Feedback,” Nature 502, 350 (2013).
- N. Roch, M. E. Schwartz, F. Motzoi, C. Macklin, R. Vijay, A. W. Eddins, A. N. Korotkov, K. B. Whaley, M. Sarovar, and I. Siddiqi, “Observation of Measurement-Induced Entanglement and Quantum Trajectories of Remote Superconducting Qubits,” Phys. Rev. Lett. 112, 170501 (2014).
- P. Kok, W. J. Munro, K. Nemoto, T. C. Ralph, J. P. Dowling, and G. J. Milburn, “Linear Optical Quantum Computing with Photonic Qubits,” Rev. Mod. Phys. 79, 135 (2007).