Crystal Defects Mimic Elusive Fractons
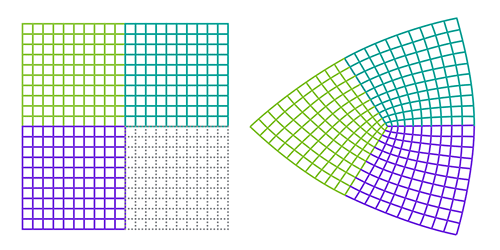
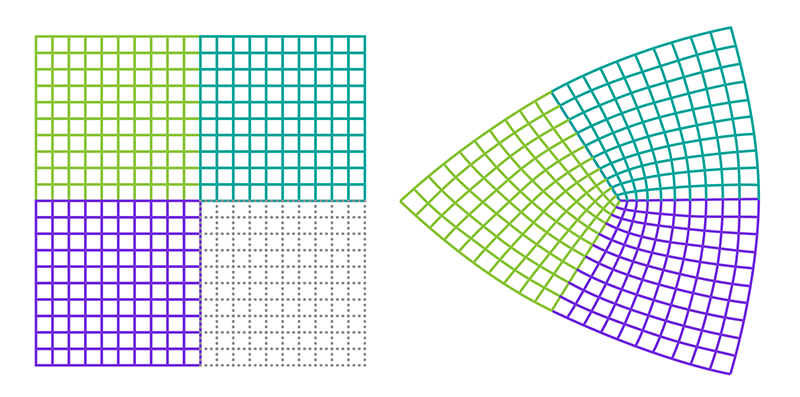
In physics, a model for one system can sometimes be mathematically mapped to a model for an entirely different system. The beauty of such a “duality” is that it allows a physical system to be pictured in an entirely different, often simpler, way. Michael Pretko and Leo Radzihovsky of the University of Colorado, Boulder, have now uncovered a visually striking duality in condensed matter physics [1]. The two researchers found a mapping between the theory for lattice defects in a 2D crystal (Fig. 1 and Fig. 2) and the theory for hypothetical particles known as fractons [2]. Fractons are expected to behave differently from the “regular” particles described by the standard model, and they might be useful for quantum computation. But they have remained an entirely theoretical construct. The existence of this duality means that some of the bizarre properties of fractons are potentially observable in crystal defects.
To provide some context for Pretko and Radzihovsky’s finding, let’s review some recent developments in condensed matter. Over the past few decades, physicists have gained a deep understanding of the particle-like excitations that can emerge from the collective behavior of particles like electrons, spins, or atoms. In some cases, these excitations behave like artificial photons or electrons [3], and there are numerous ongoing experiments to study these stunning effects [4]. However, theorists have also predicted exotic excitations that have no analog among regular particles. One such entity is the non-Abelian anyon, which doesn’t obey the quantum statistics of either a boson or a fermion. The anyons could be used to perform quantum computations by weaving them around each other [5].
A theoretical study in 2011 predicted a new kind of anyon-like excitation [6] that was soon shown to be particularly well suited for quantum-computer memory [7]. The signature of these new excitations is their constrained mobility—some of them can move, but only along certain directions, while others are completely immobile. The immobile excitations have been dubbed fractons because combining fractons tends to make them less constrained than a single fracton, as if a fracton by itself is only a fraction of a fully mobile particle [8].
Theorists have proposed various fracton models, but so far there have been no candidate materials with which to realize them in the lab. The new paper from Pretko and Radzihovsky shows that a fracton-like object—in the form of a crystal defect—may have been in front of us all along. To make the connection between defects and fractons, the duo focuses on fracton tensor gauge theory, which can be thought of as a generalization of the theory of electromagnetism [9]. Traditional electromagnetism assumes the property of gauge invariance, which enforces the conservation of electric charge. Pretko showed previously [9] that gauge invariance in certain fracton tensor gauge theories enforces the conservation of electric dipole moment—the product of the fracton’s electric charge and the fracton’s distance from an arbitrary reference point. This conservation law means that a lone fracton charge is immobile, since moving it would change its distance from the reference point and, in turn, its dipole moment. However, if there are two fractons of opposite charge, this “fracton dipole” can move while conserving the net electric dipole moment.
The crux of Pretko and Radzihovsky’s new work is showing that the theory for immobile fractons in tensor gauge theory is dual to the theory for so-called angular disclination defects in 2D crystals. To picture an isolated disclination, imagine removing an entire quadrant from a 2D square lattice and bending the remainder of the crystal to fill the space (Fig. 1). Similar to a fracton, a disclination is also immobile. But for a different reason: such a defect is stuck in place because of the immense amount of elastic energy it would take to move it through the crystal. By contrast, a pair of disclinations, or a “dislocation” (Fig. 2), can move along certain directions without a prohibitive energy cost, much like a dipole of fracton charges. The researchers also find that lattice vibrations, or phonons, of the crystal are dual to the photon-like electromagnetic excitations in the fracton theory.
Disclinations are known to form in metals and other materials as they grow or when they are deformed. But the defects tend to be in pairs (as in Fig. 2) because of the huge energy cost associated with forming a lone disclination. The new duality might inspire experimentalists to find ways of creating single disclinations, such as by rapidly solidifying a molten material or isolating one such defect from a pair.
Knowing that crystalline defects mimic fractons may not bring us closer to using fractons in quantum computers. But the duality is useful in many other ways. Most importantly, it allows us to think about fractons in terms of lattice defects and vice versa. And as we know from the particle-wave duality of quantum mechanics, some behaviors are easier to picture in one way than another. What I personally find spectacular about this new duality is its pictorial simplicity and the existence of mobility constraints on both “sides” of the duality. Looking ahead, the duality may allow older and more established results of crystal-defect theory [10] to be applied to studies of fracton physics or the other way around. Pretko and Radzihovsky have already adopted this strategy, predicting that fractons can form condensates in some fracton models. Pretko and his colleague Shriya Pai have also recently generalized the new duality to 3D and found a correspondence between disclination crystal defects in 3D and line-like (rather than point-like) fracton excitations [11].
This research is published in Physical Review Letters.
References
- M. Pretko and L. Radzihovsky, “Fracton-Elasticity Duality,” Phys. Rev. Lett. 120, 195301 (2018).
- R. M. Nandkishore and M. Hermele, “Fractons,” arXiv:1803.11196.
- M. Levin and X.-G. Wen, “Colloquium: Photons and Electrons as Emergent Phenomena,” Rev. Mod. Phys. 77, 871 (2005).
- L. Savary and L. Balents, “Quantum Spin Liquids: A Review,” Rep. Prog. Phys. 80, 016502 (2016).
- C. Nayak, S. H. Simon, A. Stern, M. Freedman, and S. Das Sarma, “Non-Abelian Anyons and Topological Quantum Computation,” Rev. Mod. Phys. 80, 1083 (2008).
- J. Haah, “Local stabilizer codes in three dimensions without string logical operators,” Phys. Rev. A 83, 042330 (2011).
- S. Bravyi and J. Haah, “Quantum Self-Correction in the 3D Cubic Code Model,” Phys. Rev. Lett. 111, 200501 (2013).
- S. Vijay, J. Haah, and L. Fu, “A New Kind of Topological Quantum Order: A Dimensional Hierarchy of Quasiparticles Built from Stationary Excitations,” Phys. Rev. B 92, 235136 (2015).
- M. Pretko, “Subdimensional Particle Structure of Higher Rank U(1) spin Liquids,” Phys. Rev. B 95, 115139 (2017).
- A. J. Beekman, J. Nissinen, K. Wu, K. Liu, R.-J. Slager, Z.Nussinov, V. Cvetkovic, and J. Zaanen, “Dual Gauge Field Theory of Quantum Liquid Crystals in Two Dimensions,” Phys. Rep. 683, 1 (2017).
- S. Pai and M. Pretko, “Fractonic Line Excitations: An Inroad from 3D Elasticity Theory,” arXiv:1804.01536.