Cloud Quantum Computing Tackles Simple Nucleus

Stefano Gandolfi

Viewpoint

Cloud Quantum Computing Tackles Simple Nucleus

Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA

May 23, 2018• Physics 11, 51

Researchers perform a quantum computation of the binding energy of the deuteron using a web connection to remote quantum devices.

Scientific computation has long been a matter of typing commands on a screen and then sending those instructions to a distant computer that might be down the hall or across the world. Remote access like this allows scientists to use supercomputers and other powerful machines that they couldn’t manage by themselves. Now this same idea has spread to the quantum realm. So-called cloud quantum computing is now being offered by several companies like IBM, Google, and Rigetti, who have quantum chips linked to the internet. A certified user simply sends his or her quantum programming code to one of these quantum providers, where the operations can be run and the results sent back. No need for the user to leave the office or even learn any of the complicated details about the quantum “hardware.” Taking advantage of this trend, Eugene Dumitrescu from Oak Ridge National Laboratory in Tennessee and collaborators have performed a computation of the deuteron binding energy using quantum processors accessed via cloud servers [1]. The solution to this problem was already known, but this is the first time this calculation has been done with quantum computers. The work highlights the opportunities for scientists as quantum machines become more and more ubiquitous.

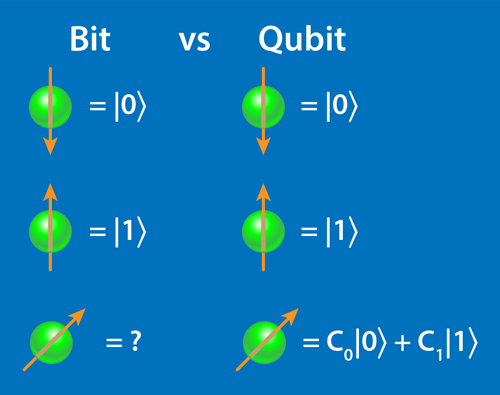
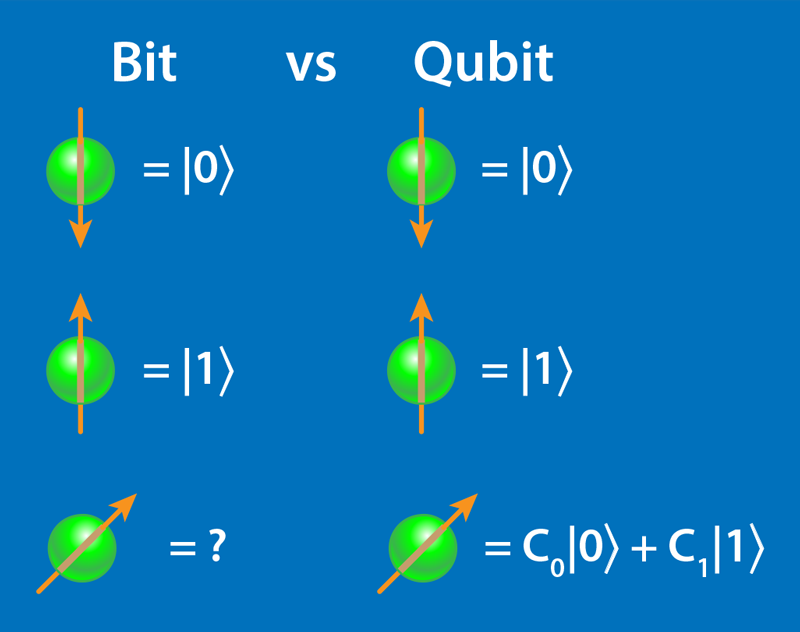
Figure caption — **Figure 1:** Both classical bits and quantum bits are characterized by two distinct states. The difference is that classical bits can only be in one state or the other, whereas a qubit can be in a combination, or superposition, of the two.

Although the idea of quantum computers has been around for decades [2], the technical realization of such machines became possible only in the last few years. Quantum computers rely on the manipulation of quantum bits, called qubits, which can be in an arbitrary superposition of the bit states, zero and one (Fig. 1). Being simultaneously in two states implies that qubits carry more information than classical bits. If you have N classical bits, then they will be in one state out of $2^{N}$ possible states, whereas N qubits could represent all those possible states at the same time. The power of quantum computers comes from their ability to create large superposition states, entanglement, and interference—all properties that do not exist in classical computation. This makes a dramatic difference in speed, as certain problems that scale exponentially in the number of operations on a classical computer are expected to scale polynomially on a quantum computer.

There now exist several realizations of quantum computers that combine classical bits with few dozens of qubits [3]. The qubits come in a variety of physical implementations, with some represented by the spin up or down of atoms and others by two excited states in a superconducting circuit, for exmple. Certain quantum machines are now available to outside users. For example, the IBM Q Experience is a cloud-based platform that allows researchers to run their own experiments on one of the superconductor-based quantum computers that are housed in different IBM research labs. In their work, Dumitrescu et al. obtained access to two cloud-based quantum computing systems: an IBM QX5 quantum chip and a Rigetti 19Q quantum chip.

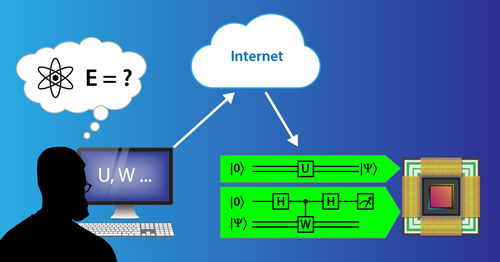
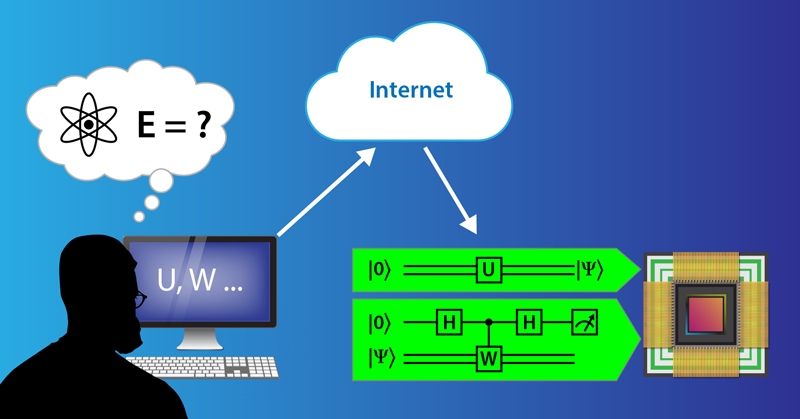
In order to utilize these machines, the researchers had to become fluent in the “language” of quantum computers, which is different from that of classical computers. In general, problem solving using quantum computers involves several steps [4–6], which can be split into three main blocks: (i) formulate the problem to be solved in terms of unitary matrices, (ii) rewrite those matrices in terms of gates that can be realized on a given quantum computer, and (iii) implement and try to improve the efficiency of (ii), reducing the number of gates as much as possible—given that a very small number of gates is enough to implement almost any unitary matrix [4].

The gate in a quantum computer refers to an operation (or manipulation) of qubits, and it is always represented by a unitary operator. If we think of the qubit state as a spin, then a unitary operator would be a rotation of that spin. To take a simple example, suppose that we want to find the energy of a particular state $|𝜓⟩$ . To construct this state, we would devise a unitary operator $U$ that would operate on one or more qubits in their ground state: $|𝜓⟩ = U |0⟩$ . Let’s assume that the Hamiltonian can be calculated from another unitary operator $W$ . An easy way to calculate the mean energy is to assemble the qubits representing $|𝜓⟩$ and manipulate them with $W$ while also manipulating an extra, or ancilla, qubit (Fig. 2). At the end of these operations, the ancilla qubit is measured, returning either zero or one. This measurement, however, is sampling just one possibility out of many, so it is necessary to repeat the measurement many times and take the average. In this case, the final output will be related to the expectation value $⟨ W ⟩$ , which could be converted to the mean energy.

Dumitrescu et al. chose as their computational target the binding energy of the deuteron [1]. The Hamiltonian in this case is very simple, and the solution can be found analytically. But formulating the problem for quantum computers is a useful exercise, which should help in developing procedures for tackling much harder problems. In terms of the three main blocks of quantum computing, the authors made a very clear and pedagogical description of points (i) and (ii), whereas point (iii) is more technical and beyond the scope of the calculation.

The team’s strategy was based on the so-called quantum eigensolver method [7]. They first represented an ansatz of the ground-state wave function in terms of a set of functions called the coupled-cluster basis [8]. This representation has one or two parameters, so they calculated the energy for different sets of parameters and chose the set that gave the lowest energy. The researchers initially performed a two-qubit computation, which involved just two coupled-cluster basis states. They found matching results from the IBM and Rigetti chips. They also performed a three-qubit computation with just the IBM chip. When the results were extrapolated to the infinite basis limit (a calculation that could be done analytically), the computed binding energy was in excellent agreement with exact calculations.

Nowadays, quantum computers are quite limited in terms of the number of qubits and available gates. In addition, it has to be said that manipulating qubits is not easy: the spin of an atom representing the state of a qubit, for example, is affected by the environment, and this means that the qubit manipulations suffer from a noise that increases with the number of gates applied to the qubits. However, even given such limitations, the interest in quantum computing has literally exploded. The amount of available quantum hardware has grown substantially as well, and this should multiply opportunities to explore new ways to solve quantum many-body problems in physics and chemistry. Researchers have already begun looking at how quantum computing could resolve problems in, for example, scattering dynamics [9] and ground-state determinations [10].

This research is published in Physical Review Letters.

References

E. F. Dumitrescu, A. J. McCaskey, G. Hagen, G. R. Jansen, T. D. Morris, T. Papenbrock, R. C. Pooser, D. J. Dean, and P. Lougovski, “Cloud Quantum Computing of an Atomic Nucleus,” Phys. Rev. Lett. 120, 210501 (2018).
R. P. Feynman, “Simulating Physics with Computers,” Int. J. Theor. Phys. 21, 467 (1982); “Quantum Mechanical Computers,” Found. Phys. 16, 507 (1986); S. Lloyd, “Universal Quantum Simulators,” Science 273, 1073 (1996).
J. S. Otterbach et al., “Unsupervised Machine Learning on a Hybrid Quantum Computer,” arXiv:1712.05771.
E. Ovrum and M. Hjorth-Jensen, “Quantum Computation Algorithm for Many-Body Studies,” arXiv:1804.03719.
P. J. Coles et al., “Quantum Algorithm Implementations for Beginners,” arXiv:1804.03719.
J. Preskill, “Quantum Computing in the NISQ Era and Beyond,” arxiv:1801.00862.
A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik, and J. L. O’Brien, “A Variational Eigenvalue Solver on a Photonic Quantum Processor,” Nat. Commun. 5, 4213 (2014).
Y. Shen, X. Zhang, S. Zhang, J.-N. Zhang, M.-H. Yung, and K. Kim, “Quantum Implementation of the Unitary Coupled Cluster for Simulating Molecular Electronic Structure,” Phys. Rev. A 95, 020501 (2017).
A. Roggero and J. Carlson, “Linear Response on a Quantum Computer,” arXiv:1804.01505.
D. B. Kaplan, N. Klco, and A. Roggero, “Ground States via Spectral Combing on a Quantum Computer,” arXiv:1709.08250.

About the Author

Stefano Gandolfi is a staff scientist working in the theoretical division of Los Alamos National Laboratory. In 2007, he obtained his Ph.D. in physics from the University of Trento, Italy, where he received an award for the best Ph.D thesis of the year. He then became a postdoctoral fellow at the International School for Advanced Studies (SISSA) in Trieste, Italy, before moving to Los Alamos in 2009. In 2013, he received the Young Scientist Prize from the International Union of Pure and Applied Physics (IUPAP). His research focuses on nuclear interactions, nuclear structure, electroweak interactions in nuclei and dense matter, physics of neutron stars, and strongly correlated ultracold Fermi gases.