PT Symmetry Goes Quantum
No physicist would tamper with the conservation of energy—the fundamental law that says energy cannot be created or destroyed. Researchers have, however, taken an interest in devices whose energy is conserved somewhat artificially. Known as PT-symmetric systems [1], these devices are engineered to have a balance of energy flowing in and out. And they feature many unusual properties, which have, for example, been harnessed to make optical components that only allow light to travel in one direction or that stop the flow of light altogether [2, 3]. Some of these properties might now be realized in the quantum domain. David Zueco of the University of Zaragoza in Spain and colleagues have proposed a realistic circuit in which microwaves interact with a quantum bit (qubit) and that would satisfy the requirements of PT symmetry [4].
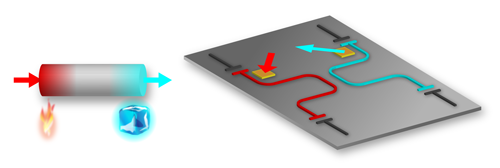
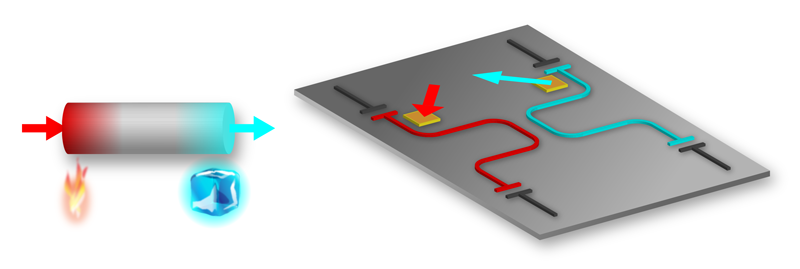
PT symmetry stands for parity-time symmetry. This terminology implies that a physical system looks exactly the same if one performs two operations on it. The first is a parity operation, which swaps left and right so as to exchange the components feeding energy in (the gain) with components allowing energy to escape (the loss). The second is time reversal, which is akin to running a “movie” of the device backwards. A simple example of a PT-symmetric system is a stick that’s being cooled on one end and heated on the other, both at exactly the same rate (Fig. 1, left). If you swap the sources performing the heating and cooling and then time reverse these processes, the system looks exactly the same.
Researchers were initially interested in whether PT symmetry could be a fundamental property of nature, a discovery that would have far-reaching consequences for quantum theory. The reason has to do with quantum theory’s underlying mathematics. Physicists have a strict requirement that the Hamiltonian—the function that is used to calculate a system’s energies—must predict real, not complex, energies. Hamiltonians having the mathematical property of being Hermitian are guaranteed to produce real energies, so quantum theory has been built on the assumption that all viable Hamiltonians are Hermitian. But it turns out that PT-symmetric Hamiltonians also predict real energies and may thus serve as a starting point for an alternative or potentially more fundamental formulation of quantum mechanics.
Textbook quantum mechanics has so far proven resilient to such attempts at a reformulation. But motivated by their potentially interesting properties, experimentalists have realized a variety of PT-symmetric devices by artificially engineering gain and loss in these systems. Most of these demonstrations have involved optical setups, since many methods exist to amplify and dampen light [2]. One experiment, for example, used two coupled ring-shaped resonators—one providing gain, the other providing loss [5]. Using such devices, researchers have explored many of the fascinating aspects of PT symmetry, such as the fact that it gives rise to “exceptional points”—conditions where a system’s allowed modes coalesce into a single mode. An optical PT-symmetric device operated near an exceptional point can behave in unconventional ways, examples of which include a laser that turns on as it incurs more loss or a “topological” waveguide that always transmits waves into a well-defined output mode irrespective of how the waves were injected [2].
Most of the devices explored so far have been comprised of macroscopic components, and any quantum effects in them were negligible. The paper from Zueco and colleagues indicates that the field is coming back to its roots, with researchers asking how a quantum device possessing PT symmetry would behave. Crucially, the appropriate device would have dynamics that could only be accurately described by the Schrödinger equation, and its gain and loss components would need to be precisely controllable in the lab. Bose-Einstein condensates [6], optomechanical systems [7], and several other setups have already been suggested for this task. Zueco and co-workers’ proposed addition to this list of possibilities may prove to be particularly attractive for studying PT symmetry and its ramifications in the quantum realm. That’s because they focus on using the tools of circuit quantum electrodynamics (QED), which is one of the fastest growing areas for studying quantum effects and making technological use of them [8]. In a circuit-QED device, single microwave photons are confined to resonant cavities. Light confined in this way can be made to interact strongly with qubit-like components that have quantized energy levels much like those of an atom.
Zueco and co-workers propose a relatively simple setup comprised of two coupled microwave cavities, each with a qubit placed nearby (Fig. 1, right) [4]. They then imagine achieving a balance of gain and loss in the resonators by driving the qubits with microwaves of the right amplitude and frequency. Using a simple model for this device, the researchers find the value of the coupling between the two resonators that will lead to a PT-symmetric phase transition and its associated exceptional point. They also predict how the transmission of a microwave signal through the circuit would be modified by the onset of this transition.
At first sight, the expected effects are not very different from those predicted by classical models of PT symmetry. But new features are expected to emerge in the quantum domain. Quantum fluctuations are intrinsically linked to both gain and loss through the fluctuation-dissipation theorem. As a result, correlations between the fluctuations of the modes that merge at an exceptional point could lead to a big enhancement in the fluctuation amplitude of the merged mode. The proposed device might also enable the study of the quantum versions of so-called chiral population transfer schemes [9, 10]. Here, one varies a device's parameters such that its allowed energies sweep out a loop around an exceptional point. The way in which the loop is cycled—say clockwise versus counterclockwise—determines the final state of the device, which could be used to build robust and broadband switching elements. By interconnecting two very active fields of research— PT symmetry and circuit QED—the new proposal puts these and other research directions within reach. If researchers succeed in making the proposed device in the lab, we would legitimately be at the starting point of the new field of PT-symmetric quantum mechanics.
This research is published in Physical Review A.
References
- C. M. Bender and S. Boettcher, “Real Spectra in Non-Hermitian Hamiltonians Having PT Symmetry,” Phys. Rev. Lett. 80, 5243 (1998).
- R. El-Ganainy, K. G. Makris, M. Khajavikhan, Z. H. Musslimani, S. Rotter, and D. N. Christodoulides, “Non-Hermitian Physics and PT Symmetry,” Nat. Phys. 14, 11 (2018).
- T. Goldzak, A. A. Mailybaev, and N. Moiseyev, “Light Stops at Exceptional Points,” Phys. Rev. Lett. 120, 013901 (2018).
- F. Quijandría, U. Naether, Ş. K. Özdemir, F. Nori, and D. Zueco, “PT-Symmetric Circuit QED,” Phys. Rev. A 97, 053846 (2018).
- B. Peng et al., “Parity–Time-Symmetric Whispering-Gallery Microcavities,” Nat. Phys. 10, 394 (2014).
- H. Cartarius and G. Wunner, “Model of a PT-Symmetric Bose-Einstein Condensate in a 𝛿-Function Double-Well Potential,” Phys. Rev. A 86, 013612 (2012).
- K. V. Kepesidis, T. J. Milburn, J. Huber, K. G. Makris, S. Rotter, and P. Rabl, “PT-Symmetry Breaking in the Steady State of Microscopic Gain–Loss Systems,” New J. Phys. 18, 095003 (2016).
- G. Wendin, “Quantum Information Processing with Superconducting Circuits: A Review,” Rep. Prog. Phys. 80, 106001 (2017).
- H. Xu, D. Mason, L. Jiang, and J. G. E. Harris, “Topological Energy Transfer in an Optomechanical System with Exceptional Points,” Nature 537, 80 (2016).
- J. Doppler, A. A. Mailybaev, J. Böhm, U. Kuhl, A. Girschik, F. Libisch, T. J. Milburn, P. Rabl, N. Moiseyev, and S. Rotter, “Dynamically Encircling an Exceptional Point for Asymmetric Mode Switching,” Nature 537, 76 (2016).