Zeroing in on the Muon’s Magnetism

B. Lee Roberts

Viewpoint

Zeroing in on the Muon’s Magnetism

Department of Physics, Boston University, Boston, MA 02215, USA

June 25, 2018• Physics 11, 65

A theoretical reevaluation of the muon’s magnetic moment gives the highest precision prediction so far, while doubling down on a discrepancy with experiments.

The muon anomalous magnetic moment $a_{𝜇}$ is an important and unique quantity in subatomic physics, since its value represents a sum over all known standard model physics. This wide sensitivity exists because the anomalous moment depends on all particles in nature that can couple to the muon, including as-yet-undiscovered ones. Theorists have precisely calculated the contribution from electrons and other particles that interact either electrically or weakly [1, 2], but they have had less success with the contribution from particles that interact through the strong force, which are called hadrons. To compute the hadronic contribution, researchers have had to resort to indirect methods that come with large uncertainties compared with those of other contributions. One of these indirect methods uses electron-positron collision data and the theory that connects these data to muon magnetic interactions. Alexander Keshavarzi from the University of Liverpool, UK, and his colleagues have performed a reevaluation of the hadronic part using the latest electron-positron collision data [3]. This work represents the most precise evaluation of the hadronic contribution, and it reaffirms a long-standing discrepancy with experiments [4]. This discrepancy may imply a contribution from new particles that would require physics beyond the standard model. The ball is now in the experimentalists’ court, as they ramp up new experiments that should measure the muon anomaly with greater precision.

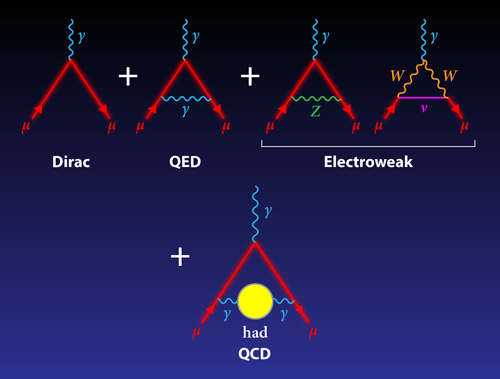
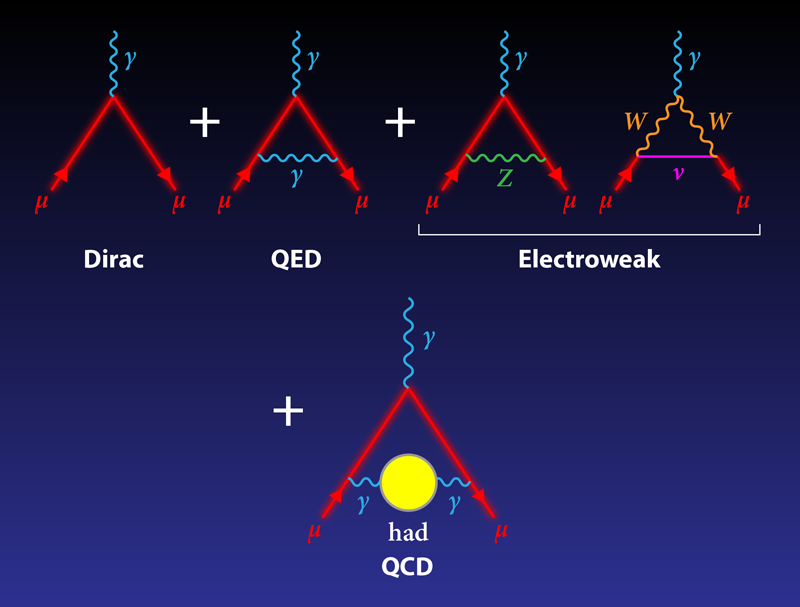
Figure caption — **Figure 1:** The magnetic moment of the muon is calculated by adding up the contributions from different sectors of the standard model. The lowest-order contribution, referred to as the Dirac part, takes into account the muon’s spin in its interaction with a magnetic field (depicted as a photon, $𝛾$ ). At higher order, virtual particles have to be considered. Depending on their interactions, these virtual particles are classified under quantum electrodynamics (QED), electroweak theory, or quantum chromodynamics (QCD). The Feynman diagrams shown here are meant to be representative of the different contributions.

The magnetic moment, at its most basic level, defines how a particle responds to a magnetic field. But at the quantum level, the moment is a probe of a wider range of physics. Early studies of the magnetic moment—specifically of the electron—provided important experimental information that led to the development of quantum electrodynamics (QED) and the standard model. The magnetic moment can be separated into two pieces, the Dirac part and the anomalous part. The Dirac part describes how a particle’s magnetic moment depends on its spin. In an elegant 1928 paper [5], Paul Dirac presented the relativistic wave equation for the electron and showed that the electron’s g value—a dimensionless constant based on the ratio of magnetic moment to spin—is exactly 2, matching the experimental data at that time. More precise measurements demonstrated that the electron’s $g$ value, $g_{e}$ , is slightly greater than 2; in other words, $g_{e} = 2 \cdot (1 + a_{e})$ , where $a_{e}$ is the electron’s magnetic anomaly. The anomalous part arises from virtual particles that couple to the electron during their fleeting existence. The value of $a_{e}$ was first derived in Julian Schwinger’s 1948 calculation [6] of the lowest-order (QED) correction, which gave the following result: $a_{e} = 𝛼 ∕ 2 𝜋 = 0.001161 \dots$ , where $𝛼$ is the fine structure constant.

The electron anomaly has been measured [7] to the subparts per billion (ppb) level, and the agreement with theory has been an important triumph of the standard model. The case with the muon is different. The muon is basically a “heavy electron,” and a crude QED calculation gives the same $g$ value for the two particles. However, the higher mass of the muon means that heavier virtual particles need to be considered when calculating $a_{𝜇}$ . Indeed, the importance of the higher-mass contributions scale as ${(m_{𝜇} ∕ m_{e})}^{2} ≃ 42, 700$ , so the measured muon anomaly is much more sensitive to a broader range of virtual particles than the electron anomaly. This is why predicting the muon anomaly requires additional calculations beyond QED [1]: there are significant contributions from particles in the electroweak [2] and strong [3] sectors, as well as potential contributions from physics beyond the standard model.

The first measurement of the muon magnetic moment—performed at the Columbia-Nevis cyclotron—showed that $g_{𝜇}$ was roughly equal to 2, but subsequent experiments at the same facility uncovered the muon’s anomalous moment [8]. The most recent measurements, performed from 1989 to 2001 at Brookhaven National Laboratory [4], gave $a_{𝜇} = 0.00116592089$ , which is slightly larger than $a_{e}$ because of the higher mass contributions. In response to the ever-increasing precision of experiments, the theoretical community has been pushed to go to ever-higher order (and precision) in their calculations. Each order can be thought of as added “loops” of virtual particles in the Feynman diagrams that provide a shorthand for particle physics computations. For virtual QED particles, the necessary precision requires going to five loops, which translates into computations of some 12,672 Feynman diagrams [1]. For virtual electroweak particles, theorists have worked out the two-loop diagrams [2], which, unlike the one-loop diagrams, are sensitive to the Higgs mass.

For hadrons, which interact through the strong force, the problem is more complicated. The reason has to do with the theory of the strong interaction, quantum chromodynamics (QCD), which can’t be solved at the low-energy scale set by the muon mass (100 MeV). Theorists have devised two ways to go around this limitation. The first of these indirect methods is so-called lattice QCD, which is a way of computing strong interactions by assuming that particles live on a discrete lattice. Some recent lattice QCD papers have calculated the hadronic contributions [9], but the error bars remain quite large. The other indirect method is the one employed by Keshavarzi et al. [3]. In this approach, researchers use data from electron-positron colliders, focusing on events that produce hadrons. Because these hadron-producing events can be related to the muon interaction with virtual hadrons, researchers can convert the electron-positron data into a prediction for the hadron contribution to the muon anomaly [3, 10].

Increasing the precision of the lowest-order hadronic correction has depended on new experiments that measure electron-positron production of hadrons. (The most important production channels involve two pions, but other channels contribute.) The last major published evaluations of the world data sets appeared in 2011 [11], and significantly more experimental data have become available since then [6]. Keshavarzi et al. [3], as well as others [10], have incorporated the most recent data into their analyses. The latest results give a predicted standard model value of $a_{𝜇} = 0.00116591820$ , which is 3.7 standard deviations smaller than the experimental value [4]. The central value of the standard model prediction has remained stable since 2003 (see Fig. 24 of Ref. [3]). However, the uncertainty has been steadily decreasing, which means that the statistical significance of the difference between the standard model and the experimental values [4] has continued to increase.

This new analysis of the lowest-order hadronic contribution represents another important step in the worldwide effort to improve theoretical predictions of the hadronic contribution and thereby predictions of the standard-model value of the muon anomaly. Several new electron-positron data sets are being prepared for publication, and significant work continues to improve the lattice QCD computations. An international collaboration, called the Muon g-2 Theory Initiative, is bringing together all of the parties actively working toward a more precise value of the hadronic contribution. The collaboration plans to release a combined result from all analyses in 2019. On the experimental side, an increase in precision on $a_{𝜇}$ is expected from the new Fermilab and J-PARC experiments, with the first result expected from Fermilab in 2019. It may turn out that the muon will open a window to the new physics that is desperately being sought in high-energy experiments like the Large Hadron Collider and in precision experiments across the world.

This research is published in Physical Review D.

References

T. Aoyama, M. Hayakawa, T. Kinoshita, and M. Nio, “Complete Tenth-Order QED Contribution to the Muon $g - 2$ ,” Phys. Rev. Lett. 109, 111807 (2012).
C. Gnendiger, D. Stöckinger, and H. Stöckinger-Kim, “The Electroweak Contributions to $(g - 2) 𝜇$ after the Higgs-Boson Mass Measurement,” Phys. Rev. D 88, 053005 (2013), and references therein..
A. Keshavarzi, D. Nomura, and T. Teubner, “The Muon $g - 2$ and $𝛼 (M_{Z}^{2})$ : A New Data-Based Analysis,” Phys. Rev. D. 97, 114025 (2018).
G. W. Bennett et al., “Final Report of the E821 Muon Anomalous Magnetic Moment Measurement at BNL,” Phys. Rev. D 73, 072003 (2006).
P. A. M. Dirac, “The Quantum Theory of the Electron,” Proc. R. Soc. London A 117, 610 (1928).
J. Schwinger, “On Quantum-Electrodynamics and the Magnetic Moment of the Electron,” Phys. Rev. 73, 416 (1948).
D. Hanneke, S. Fogwell, and G. Gabrielse, “New Measurement of the Electron Magnetic Moment and the Fine Structure Constant,” Phys. Rev. Lett. 100, 120801 (2008).
R. L. Garwin, L. M. Lederman, and M. Weinrich, “Observations of the Failure of Conservation of Parity and Charge Conjugation in Meson Decays: The Magnetic Moment of the Free Muon,” Phys. Rev. 105, 1415 (1957); R. L. Garwin, D. P. Hutchinson, S. Penman, and G. Shapiro, “Accurate Determination of the $𝜇^{+}$ Magnetic Moment,” 118, 271 (1960).
Sz. Borsanyi et al., “Hadronic Vacuum Polarization Contribution to the Anomalous Magnetic Moments of Leptons from First Principles,” arXiv:1711.04980 [Phys. Rev. Lett. (to be published)]; T. Blum et al., “Calculation of the Hadronic Vacuum Polarization Contribution to the Muon Anomalous Magnetic Moment,” arXiv:1801.07224 [Phys. Rev. Lett. (to be published)].
M. Davier, A. Hoecker, B. Malaescu, and Z. Zhang, “Reevaluation of the Hadronic Vacuum Polarisation Contributions to the Standard Model Predictions of the Muon $g - 2$ and $𝛼 (m_{Z}^{2})$ Using Newest Hadronic Cross-Section Data,” Eur. Phys. J. C 77, 827 (2017); F. Jegerlehner, “Muon $g - 2$ Theory: The Hadronic Part,” EPJ Web Conf. 166, 00022 (2018).
M. Davier, A. Hoecker, B. Malaescu, and Z. Zhang, “Reevaluation of the hadronic contributions to the muon $g - 2$ and to $𝛼 (M_{Z}^{2})$ ,” Eur. Phys. J. C 71, 1515 (2011); K. Hagiwara, R. Liao, A. D. Martin, D. Nomura, and T. Teubner, “ $(g - 2) 𝜇$ and $𝛼 (M_{Z}^{2})$ Re-Evaluated Using New Precise Data,” J. Phys. G 38, 085003 (2011).

About the Author

Lee Roberts is Professor of Physics at Boston University. His undergraduate degree is from the University of Virginia, and his Ph.D. is from the College of William and Mary. He held postdoctoral positions at the Rutherford High Energy Laboratory (now the Rutherford Appleton Laboratory) and the MIT Laboratory for Nuclear Science, before moving to Boston University. He played a leadership role in the Brookhaven Muon g-2 experiment E821 from 1989 until 2007 and, more recently, in the new Fermilab g-2 experiment E989.