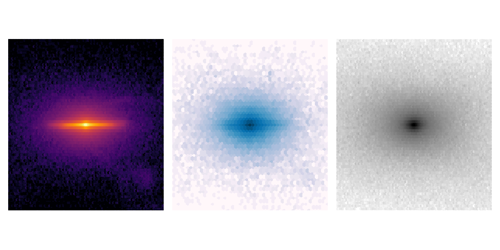
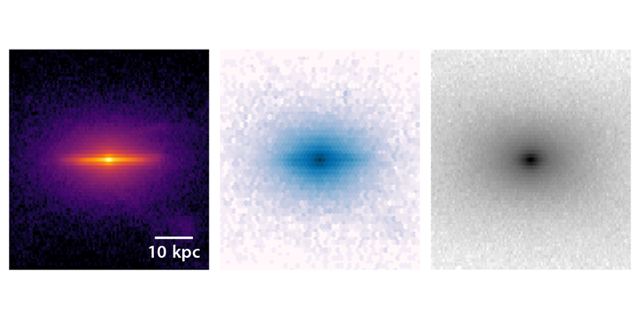
A Dark Matter Speedometer
Most matter in the Milky Way and other galaxies is invisible matter. For nearly a century, astronomers have deduced the existence of such dark matter by measuring its gravitational influence on the visible stars and gas within galaxies [1]. And high-powered telescopes now routinely make detailed maps of where this dark matter is located [2]. But how fast dark matter moves—a quantity that affects the interpretation of dark matter detection experiments—is less well understood. To this point, astrophysicists have estimated the characteristic speed of dark matter using simple theoretical ideas [3]. A new study by Jonah Herzog-Arbeitman from Princeton University, New Jersey, and colleagues [4] now comes at this question from a different perspective. Using numerical simulations, the researchers identify “old” stars in the Galaxy that share the same characteristic speed as the dark matter, thereby providing a new window into the dark side of our Galaxy.
Although there is overwhelming evidence for dark matter, the particles that make up this form of matter have yet to be directly detected. The so-called weakly interacting massive particle (WIMP) is a theoretically predicted elementary particle with mass anywhere from tens to hundreds of times that of a proton, and it is a longstanding dark matter candidate particle. Many direct-detection experiments around the world are collecting data, searching for the rare scattering of WIMP-like dark matter particles off atomic nuclei in earthbound detectors [5]. Although such searches have come up empty handed, modern experiments are setting impressive bounds on the strength of the WIMP-nucleus interaction.
The number of scattering events between a dark matter particle and a nucleus depends on the strength of their interaction, the scattering cross section, which is governed by the microphysical theory of dark matter. But it also depends on the large-scale properties of dark matter, such as its density and characteristic speed in the Solar System. Observations have revealed that the local dark matter density, as obtained from the motion of stars near the Sun, is approximately 0.01 solar masses per cubic parsec [6]. This is equivalent to about one dark matter particle in the volume of a coffee cup. However, it has been difficult to measure the speed distribution of the local dark matter. This distribution is ultimately a reflection of how the dark matter assembles to form the Galaxy. Direct-detection experiments typically assume that the dark matter speed distribution is a Maxwell-Boltzmann distribution [7], like that of air molecules moving in a room, but this is just an educated guess.
However, astrophysicists can estimate the local speed distribution of dark matter using numerical simulations of the formation of the Milky Way. These simulations start out with a volume of dark and visible matter that spans scales much larger than the size of the Milky Way. Within this larger volume, objects that have similar mass and structure to our Galaxy are identified. The simulations then zoom in on these Milky-Way-like objects and re-simulate them at much higher spatial resolution than the initial volume. By examining the behavior of dark matter particles near the Sun, zoom-in simulations that only include dark matter have shown that the local dark matter speed distribution differs from a Maxwell-Boltzmann distribution [8, 9] by having fewer fast-moving particles and more slow-moving particles. However, simulations that include the physics of stars and gas show that the dark matter speed distribution may be closer to the Maxwell-Boltzmann model. Settling this issue has important implications for direct-detection experiments because it is the highest speed particles that are the easiest to detect.
But what speed distribution does nature follow? This is where the work of Herzog-Arbeitman and colleagues comes in. The authors utilize a zoom-in simulation of the Milky Way (Fig. 1), which accounts for the gravitational physics of both the dark and visible matter as well as for some aspects of the electromagnetic interactions between the stars and gas. Just like in the real Milky Way, the stars that form in these simulations fall into two types: older stars with fewer heavy elements than the Sun and younger stars with more heavy elements than the Sun (note that astronomers refer to heavy elements as those that are more massive than helium [10]). From the simulations, the team computes the speed distribution of the different types of stars as well as that of the dark matter. They find an interesting trend: the speed distribution of the dark matter particles nearly matches that of the oldest stars in the Galaxy. Thus, by measuring the speeds of the oldest stars using data from astronomical surveys, one can effectively measure the speeds of the dark matter particles. The realization that old stars and dark matter share the same speed may be related to the fact that both have been around since the earliest epochs of the formation of the Galaxy and have relaxed to the same equilibrium distribution.
Herzog-Arbeitman and colleagues’ results represent a crucial first step toward connecting the speed of particles in the dark sector of our Galaxy to that of stars in the visible sector. They provide direct-detection experimentalists with a method to empirically estimate the dark matter speed distribution, which is important for interpreting the data. But there is more work to be done on this topic. On the simulations front, it will be important to implement more of the detailed physics of the electromagnetic interactions between the stars and gas, which affect the speed distributions of the stars and the gas and, in turn, that of the dark matter. Further, it will be important to analyze more simulated galaxies in the future in order to obtain statistically significant speed distributions. On the observational front, it will be interesting to see precise measurements of the speed distribution of the oldest stars using forthcoming data from the second data release of the GAIA survey [11]. With new data and improved simulations, studies such as that of Herzog-Arbeitman and co-workers, which connect the large-scale properties of dark matter to direct-detection experiments, will become increasingly crucial in our journey toward identifying the nature of dark matter.
This research is published in Physical Review Letters.
References
- F. Zwicky, “Die Rotverschiebung von Extragalaktischen Nebeln,” Helv. Phys. Acta 6, 110 (1933).
- D. Clowe, M. Bradač, A. H. Gonzalez, M. Markevitch, S. W. Randall, C. Jones, and D. Zaritsky, “A Direct Empirical Proof of the Existence of Dark Matter,” Astrophys. J. 648, 109 (2006).
- M. Lisanti, L. E. Strigari, J. G. Wacker, and R. H. Wechsler, “Dark Matter at the End of the Galaxy,” Phys. Rev. D 83, 023519 (2011).
- J. Herzog-Arbeitman, M. Lisanti, P. Madau, and L. Necib, “Empirical Determination of Dark Matter Velocities Using Metal-Poor Stars,” Phys. Rev. Lett. 120, 041102 (2018).
- L. Baudis, “Direct Dark Matter Detection: The Next Decade,” Phys. Dark Univ. 1, 94 (2012).
- J. I. Read, “The Local Dark Matter Density,” J. Phys. G 41, 063101 (2014).
- J. D. Lewin and P. F. Smith, “Review of Mathematics, Numerical Factors, and Corrections for Dark Matter Experiments Based on Elastic Nuclear Recoil,” Astropart. Phys. 6, 87 (1996).
- M. Vogelsberger, A. Helmi, V. Springel, S. D. M. White, J. Wang, C. S. Frenk, A, Jenkins, A. Ludlow, and J. F. Navarro, “Phase-Space Structure in the Local Dark Matter Distribution and its Signature in Direct Detection Experiments,” Mon. Not. R. Astron. Soc. 395, 797 (2009).
- Y.-Y. Mao, L. E. Strigari, and R. H. Wechsler, “Connecting Direct Dark Matter Detection Experiments to Cosmologically Motivated Halo Models,” Phys. Rev. D 89, 063513 (2014).
- A. Frebel and J. E. Norris, “Near-Field Cosmology with Extremely Metal-Poor Stars,” Annu. Rev. Astron. Astrophys. 53, 631 (2015).
- M. A. C. Perryman, K. S. de Boer, G. Gilmore, E. Høg, M. G. Lattanzi, L. Lindegren, X. Luri, F. Mignard, O. Pace, and P. T. de Zeeuw, “GAIA: Composition, Formation and Evolution of the Galaxy,” Astron. Astrophys. 369, 339 (2001).