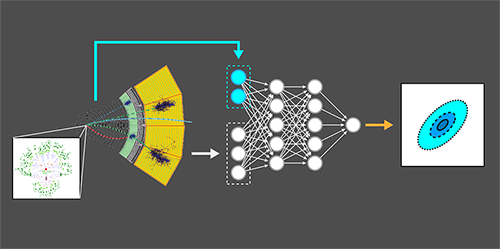
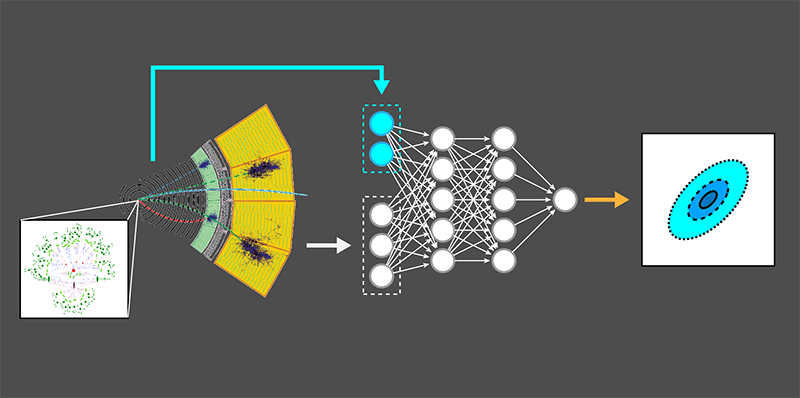
Fast-Forwarding the Search for New Particles
In the eyes of an old and famous statistics paper [1], searching for evidence of a new particle in the complex data of the Large Hadron Collider should be easy. You just need to calculate two numbers: the likelihood that the data came from the hypothetical particle and the likelihood that it did not. If the ratio between these numbers is high enough, you’ve made a discovery. Can it really be that easy? In principle, yes, but in practice, the two likelihood calculations are intractable. So instead, particle physicists approximate the likelihood ratio by making simplifying assumptions. Even then, the calculation requires a huge amount of computer time. In a pair of papers [2], Johann Brehmer of New York University and colleagues propose a new approach that avoids the typical simplifications and doesn’t demand long computation times. Their method, which relies on machine-learning tools, could significantly boost physicists’ power to discover new particles in their data.
Physicists almost never directly “see” the particle that they are searching for. That’s because new particles created in a collision exist for only a brief shining moment ( s) before decaying into other particles. These secondary particles may lead to hundreds of other particles, which are what’s actually picked up in the detectors. When making a likelihood calculation, researchers have to account for all of the different types of secondary particles with different momenta that could have led to the same detected outcome—a bit like sipping a glass of wine and trying to imagine all of the ways the Sun and weather could have influenced its flavor. Accounting for all of the possible secondary particles and their momenta involves a hairy integral that sums over all of the possibilities. Unfortunately, calculating the integral exactly is impossible, and numerical approaches fail because of the vast parameter space of the unobserved particles.
Obviously, particle physicists have not thrown their hands in the air and given up. They’ve managed to extract evidence from the collider data for all of the particles that make up the standard model, including the Higgs boson. The key to this success has been simplifying the relevant likelihood-ratio calculation into one that is still computationally expensive, but doable—albeit with less statistical power to make a detection. The most widespread approach has been to randomly select a few of the possibilities for the unobserved secondary particles and momenta and then to use these possibilities to simulate detector data with or without a new particle [3]. These simulations still take up a lot of computer time. And, most importantly, they cannot describe the expected data in terms of all of the relevant parameters, which is where the discovery power is lost. An alternative approach attempts to tackle the integration directly [4], making it tractable via a series of assumptions about the secondary states, such as whether the particles involved can be treated independently. This direct approach also requires significant computational resources, and the assumptions are viewed as unpalatable.
In their two papers, Brehmer and co-workers outline a new strategy for calculating the likelihood ratio within effective field theories, which are often used for making predictions beyond the standard model. They first point out that even though the likelihood ratio’s numerator and denominator are intractable, the difficult bits in both cancel out in an “extended” version of the final ratio. In this expression, some momenta of the unobserved particles are assumed to be constant. The extended ratio can be calculated using a small number of integrals, and the original likelihood ratio can then be recovered from the extended version using machine learning (Fig. 1). In a nutshell, a neural network is provided with many simulated examples of the few unobserved momenta so that it learns how to approximate the intractable likelihood ratio—much as though it had learned how to do the integral! The researchers have, in a sense, combined the best of the simulation and direct approaches. At the same time, they avoid the pitfalls of existing approaches: the trained neural network evaluates the likelihood ratio quickly (within microseconds), without using the simplifying assumptions of the direct calculation approach.
Can particle physicists now jump for joy, knowing future searches will be a lot easier? Not quite, as the proposed approach comes with some costs. It will require the generation of many simulated examples in order for the neural network to learn the relationship between the unobserved and observed data. In addition, the approach uses complex machine-learning algorithms, which can be difficult to train and understand. To what extent it will actually be faster is hard to predict at this point. But in my view, this is a landmark new idea, which brings the power of modern machine-learning to bear on a central, intractable statistical problem in particle physics. It suggests that we can extract more information out of our collisions and at a reduced computational cost. The possibility of more discoveries, in less time and for less money, is definitely good news.
This research is published in Physical Review Letters and Physical Review D.
References
- J. Neyman and E. S. Pearson, “On the problem of the most efficient tests of statistical hypotheses,” Phil. Trans. R. Soc. Lond. A. 231, 289 (1933).
- J. Brehmer, K. Cranmer, G. Louppe, and J. Pavez, “Constraining effective field theories with machine learning,” Phys. Rev. Lett. 121, 111801 (2018); J. Brehmer, K. Cranmer, G. Louppe, and Juan Pavez, “A guide to constraining effective field theories with machine learning,” Phys. Rev. D 98, 052004 (2018).
- S. Agostinelli et al., “Geant4: A simulation toolkit,” Nucl. Instrum. Methods A 506, 250 (2003).
- K. Kondo, “Dynamical likelihood method for reconstruction of events with missing momentum. I. Method and toy models,” J. Phys. Soc. Jpn. 57, 4126 (1988); “Dynamical likelihood method for reconstruction of events with missing momentum. II. Mass spectra for processes,” 60, 836 (1991); R. H. Dalitz and G. R. Goldstein, “Decay and polarization properties of the top quark,” Phys. Rev. D 45, 1531 (1992); V. M. Abazov et al. (DØ Collaboration), “A precision measurement of the mass of the top quark,” Nature 429, 638 (2004).