Surfing on a Wave of Quantum Chaos

Xiaoliang Qi

Viewpoint

Surfing on a Wave of Quantum Chaos

Stanford Institute for Theoretical Physics, Stanford University, Stanford, CA 94305, USA

September 16, 2019• Physics 12, 101

A model based on Brownian motion describes the tsunami-like propagation of chaotic behavior in a system of quantum particles.

Figure caption — **Figure 1:** Sketch of the “operator scrambling” concept. In a chaotic system, an operator that flips a single qubit at time 0 evolves in time into a more complex operator that flips more qubits.

In daily life, “chaos” describes anything messy. In physics, the term has a more specific meaning: It refers to systems that, while subject to deterministic laws, are totally unpredictable because of an exponential sensitivity to initial conditions—think of the butterfly flapping its wings and causing a distant tornado. But how does the chaos observed in the classical, macroscopic world emerge from the quantum-mechanical laws that govern the microscopic world? A recently proposed explanation invokes quantum “information scrambling” [1, 3], in which information gets rapidly dispersed into quantum correlations among the particles of a system. This scrambling is a memory-loss mechanism that can cause the unpredictability of chaos. Developing a theory that fully describes information scrambling remains, however, a daunting task. Now, Shenglong Xu and Brian Swingle of the University of Maryland, College Park, have taken a step toward this description by studying chaos with models based on a quantum version of Brownian motion [4]. Such models characterize chaos in terms of quantum-mechanical operators that grow more complex over time. Xu and Swingle show that this formalism enables a quantitative description of how chaos spreads in a many-body system.

In classical physics, a familiar example of chaos is the three-body problem: When two planets orbit a star, the motion of the system is extremely sensitive to the bodies’ initial positions and momenta. The future positions and momenta are deterministically related to the initial conditions, but this connection grows more mathematically complex with time.

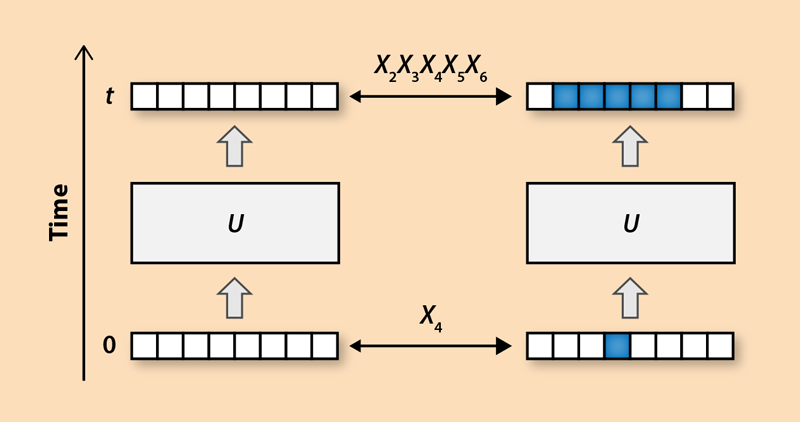
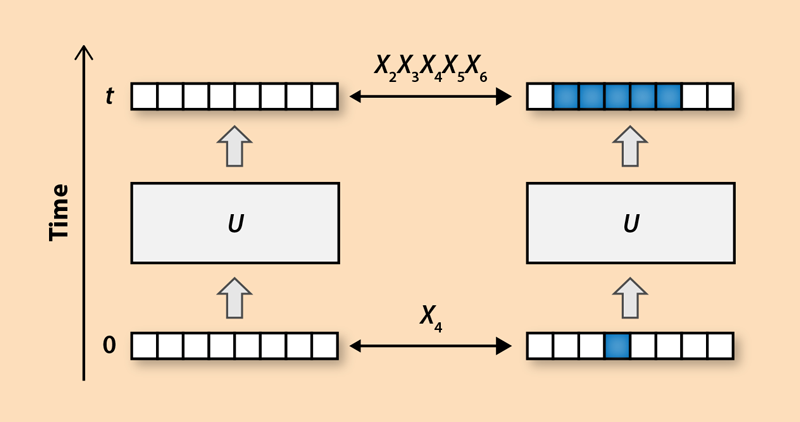
It is natural to ask whether a counterpart of chaos exists in the quantum world. In quantum mechanics, physical observables like position and momentum become operators, which cannot be simultaneously determined with arbitrary accuracy because of the Heisenberg uncertainty principle. However, the dynamics remain deterministic, since operators at a later time are determined by the initial operators. Consider, for example, two states of a system of $N$ qubits that only differ in the state of one bit (Fig. 1). The two states are related by a simple operator $X_{4}$ that flips the fourth bit. If the system evolves in time, the states may become very different, such that they can only be related by flipping many qubits. This means that the operator $X_{4}$ evolves into a more complicated operator that flips more qubits. Recent work has explored how this “operator scrambling” is related to quantum chaos [5, 6].

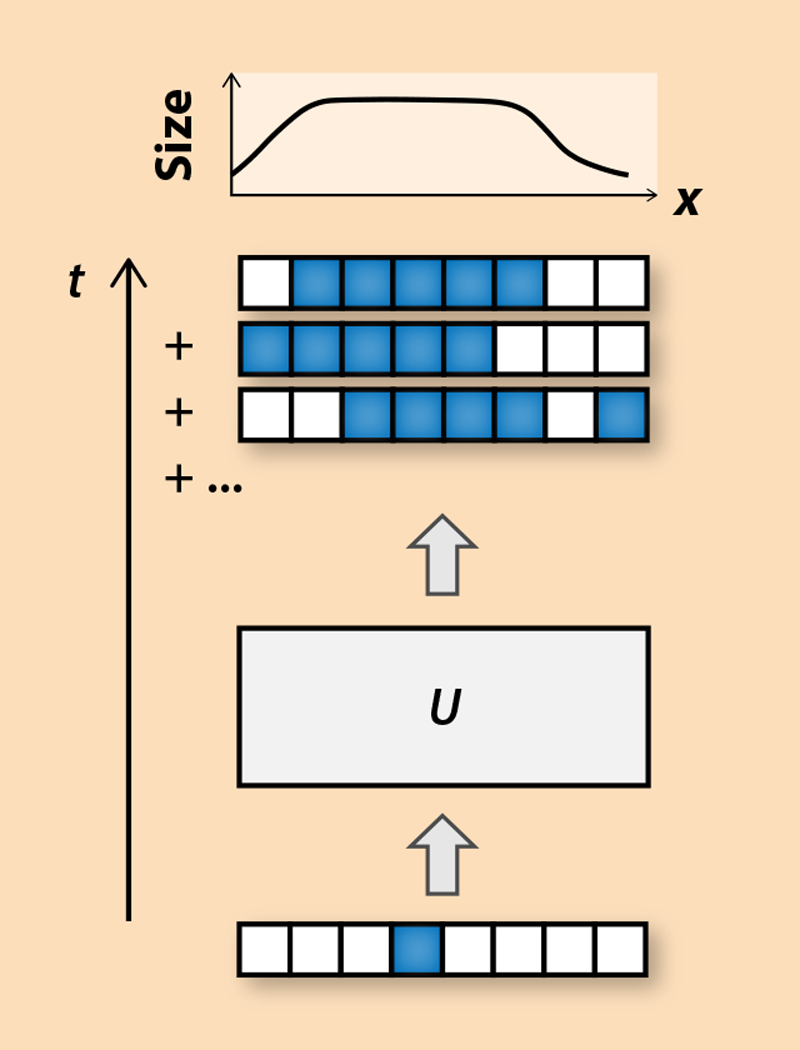
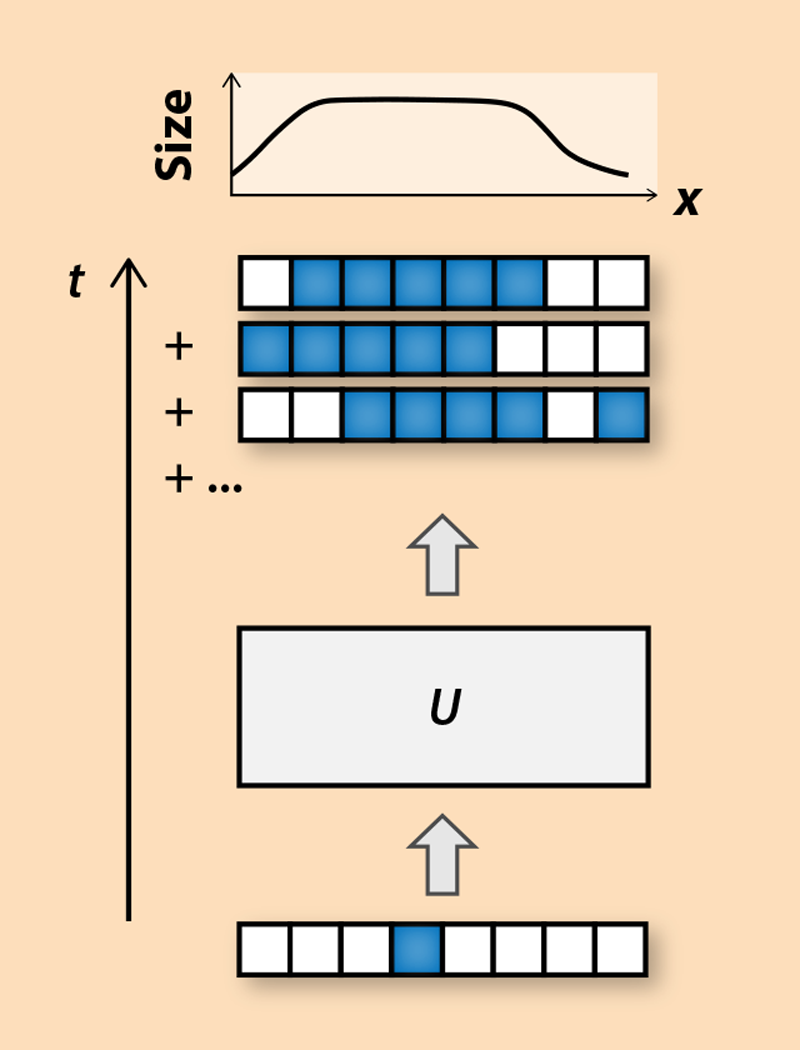
Such studies have hinted at some characteristic features of quantum chaos. In a system of qubits, such as an ensemble of electron spins in a crystal, flipping a single qubit (or a few qubits) in a chaotic system is like triggering a localized earthquake in the middle of the ocean. Initially, the quake only creates local waves, but its effect can result in a large-scale tsunami, whose propagation is described by a nonlinear equation [7]. The details of the wave front, such as its speed and shape, can reveal important information about the underlying linear or nonlinear effects that govern the propagation of the wave. Similar behavior is expected in the dynamics of quantum operators (Fig. 2). Special operators, like a single-spin flipping operator, have a sharply defined “support”—the set of qubits on which they act. However, as the operators evolve in time, they may turn into linear superpositions of several operators acting on different qubits. Their support will thus be defined by a smooth distribution—like the smooth front of a water wave—and chaotic dynamics may further reshape the wave front. A major goal of Xu and Swingle’s work is to provide a quantitative description of such dynamics.

Studying operator scrambling is a difficult task, because chaotic systems are hard to tackle analytically and numerically. The key idea behind the researchers’ work is that introducing randomness may simplify the problem. The advantages of such an approach are known from thermodynamics: While it is impossible to describe the exact state of gas molecules in a room, one can predict the relation between the gas pressure and temperature with high accuracy by assuming a random distribution of the particles’ states. Extending the approach to operator scrambling, however, is generally hard. Even determining how much the size of an operator changes after a short time can be difficult, because information from the past can have a complex effect on the future.

To overcome these difficulties, Xu and Swingle turn to so-called Brownian coupled cluster (BCC) models. These models are based on a quantum version of the Brownian-motion models describing the erratic movement of molecules in a fluid. In BCC models, the Hamiltonian governing the system’s dynamics is not constant but is drawn randomly from an ensemble of suitable Hamiltonians at each time instant [8]. Loosely speaking, this is like shuffling cards after each round in a card game. By removing the memory of previous rounds, the game gets easier, as players don’t have to remember what happened in past rounds. . The researchers adapt BCC models to provide a description of chaotic information scrambling. In their mathematical derivation, this memory erasure simplifies the dynamics of the system, such that the spreading of chaos can then be characterized by a single differential equation.

Xu and Swingle focus on a family of Hamiltonians that describe spins with random, local coupling between them. Using this family, they analyze systems of quantum particles with $N$ degrees of freedom and compare the results for large $N$ ( $N ≫ 1$ ) and small $N$ ( $N = 2$ corresponds to a conventional qubit). Starting with infinitely large $N$ —to simplify the analysis—they determine that the wave front moves as a solitary wave without changing shape. This infinite- $N$ limit is unstable, however, and for any finite $N$ , they find a wave front that becomes smoother and smoother as time goes on. With further approximations, they tackle the case of small $N$ , which is analytically harder, finding similar wave propagation and dissipation features.

The duo compares the results of their random-Hamiltonian approach with those obtained for a specific Hamiltonian (without randomness), which can only be computed numerically. The comparison shows qualitative agreement between the two cases, supporting the validity of the BCC approach. It is important to note, however, that there is a fundamental difference between Brownian models and Hamiltonian models without randomness: in the latter, the energy of the system is not conserved. As the authors suggest, future work may look into developing frameworks that could quantitatively describe quantum chaos while respecting energy conservation.

There are many reasons why a more quantitative and systematic understanding of quantum chaos will be important. One of them is related to an important line of fundamental research. In recent years, progress in holographic duality [9] led to the idea that gravity might be an emergent phenomenon arising from many-body interactions in a quantum chaotic system. Theorists showed, for instance, that an object falling into a black hole causes a perturbation to the event horizon that’s similar to the propagation of a chaotic wave front [3, 10]. By helping us model quantum chaos, the new operator scrambling approach may contribute to unlocking the mystery of quantum gravity.

This research is published in Physical Review X.

References

P. Hayden and J. Preskill, “Black holes as mirrors: quantum information in random subsystems,” J. High Energ. Phys. 2007, 120 (2007).
Y. Sekino and L Susskind, “Fast scramblers,” J. High Energ. Phys. 2008, 065 (2008).
S. H. Shenker and D. Stanford, “Black holes and the butterfly effect,” J. High Energ. Phys. 2014, 67 (2014).
S. Xu and B. Swingle, “Locality, quantum fluctuations, and scrambling,” Phys. Rev. X 9, 031048 (2019).
D. A. Roberts, D. Stanford, and A. Streicher, “Operator growth in the SYK model,” J. High Energ. Phys. 2018, 122 (2018).
A. Nahum, S. Vijay, and J. Haah, “Operator spreading in random unitary circuits,” Phys. Rev. X 8, 021014 (2018).
H. Liu and S. J. Suh, “Entanglement tsunami: Universal scaling in holographic thermalization,” Phys. Rev. Lett. 112, 011601 (2014).
An analogous family of model with discrete time steps, named as random circuits, have been studied in literature (see Ref. [6]).
J. Maldacena, “The large $N$ limit of superconformal field theories and supergravity,” Int. J. Theor. Phys. 38, 1113 (1999).
D. A. Roberts, D. Stanford, and L. Susskind, “Localized shocks,” J. High. Energ. Phys. 2015, 51 (2015).

About the Author

Xiaoliang Qi is a professor of physics at Stanford University. He received his Ph. D. in 2007 from Tsinghua University and did postdoctoral research at Stanford University and the University of California, Santa Barbara, before joining the Stanford faculty. His current research focuses on the relations between quantum entanglement, quantum chaos, and quantum gravity. https://profiles.stanford.edu/xiaoliang-qi