Cosmic Predictions from the String Swampland

The puzzles that keep particle physicists busy come in different forms. For example, the standard model contains 12 gauge bosons, or force carriers, that comprise the photon, the weak vector bosons, and the gluons. But why is the size of this gauge group so “small”? If all gauge groups are mathematically possible and none more probable than any other, then a more likely size would be very large, if not infinite! Even if one accepts the gauge group as given, one still has to explain where the observed masses and couplings of the standard model particles come from. The mass of the Higgs boson in particular is hard to understand. If one calculates the Higgs mass—taking into account various quantum corrections, such as quantum loops—the expected value should be close to the Planck mass: $M_P=\sqrt{\frac{\hslash c}{G}}\approx 10^{18}$ $\text{GeV}∕c^2$, which is 16 orders of magnitude greater than the observed value. This large discrepancy is often called the hierarchy problem. To make the quantum corrections disappear, one has to fine-tune the parameters in the theory. Similar fine-tunings are deemed necessary to explain cosmological parameters, like dark energy and the age of the Universe.

Avoiding these fine-tunings has motivated particle physicists to look for QFTs that include the standard model but go beyond it in some way. For example, one of the ideas proposed to explain the smallness of the observed Higgs mass is to assume the existence of so-called supersymmetric particles, which would help cancel the quantum corrections that lead to the large expected mass. However, the prospects for discovering supersymmetric particles seem bleak at best, as searches for them in collider experiments have come back empty-handed.

It is fair to say that, despite many decades of efforts by brilliant physicists, a beyond-standard-model QFT that solves the fine-tuning problems has not been found. Perhaps this lack of success is due to gravity being left out of the alternative-model building. The argument for ignoring gravity has been that gravitational interactions between particles only become relevant at extremely high energies. However, a QFT that is consistent with known physics at low energy should presumably be consistent with gravity once the energy is ramped up. Performing such a consistency check with gravity can guide beyond-standard-model searches—and lead to surprises—as evidenced by recent results from string theory.

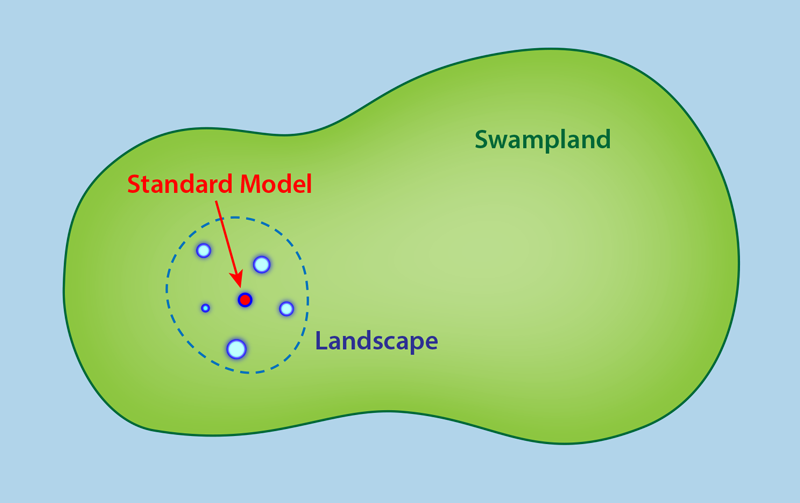
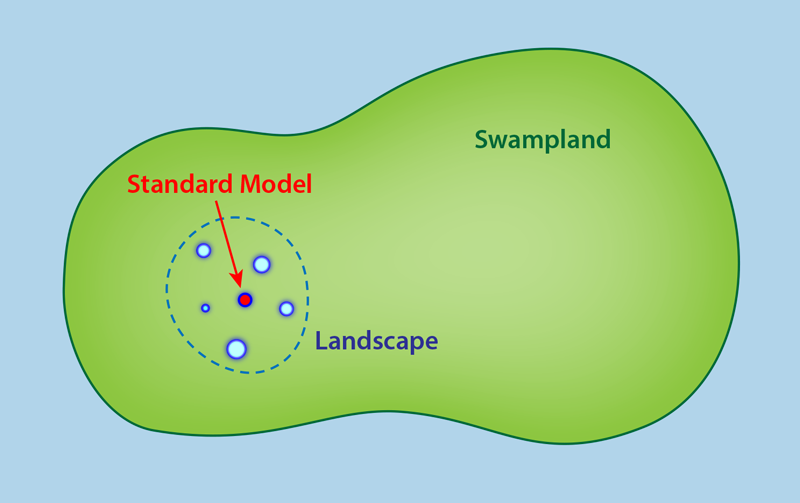
String theory is the most promising candidate for a consistent quantum theory of gravitationally interacting matter fields. The theory is defined in 10 or 11 space-time dimensions, which means we need to compactify the extra dimensions (for example, by curling them up into tiny circles) so as to be consistent with our four-dimensional Universe. Different compactification scenarios produce different low-energy four-dimensional quantum field theories, which together form the so-called “string landscape” (Fig. 1). Somewhere within this string-consistent region is the standard model QFT. But how big is the landscape? Does it contain all possible QFTs? If the answer were yes, then string theory would not offer much insight into how to go beyond the standard model. However, as it turns out there is growing evidence that we cannot get all QFTs as low-energy limits of string compactifications [1, 2], and in fact the overwhelming majority of QFTs belong to the swampland that is outside of the landscape (Fig. 2).

APS/Alan Stonebraker

APS/Alan Stonebraker

×

Determining the criteria that distinguish landscape QFTs from swampland QFTs is one of the active areas of research in string theory today. Since we do not know the full list of consistent compactifications of string theory, we cannot be sure about the exact conditions delimiting the boundaries between these two regions. But we can take an empirical approach by examining the large class of reliable compactifications that decades of string theory research have provided and see if there are common features among the resulting low-energy QFTs. From this, we can come up with universal criteria for deciding which QFTs reside in the swampland or the landscape. An example of such criteria is the weak gravity conjecture, which says that gravity is always the weakest force in any string-consistent QFT [3]. Some evidence for this conjecture comes from studies of black hole physics and their thermodynamical properties. And, recently, additional support for the weak gravity conjecture has emerged from numerical simulations that show how gravity’s relative weakness to other forces can prevent naked singularities from occurring [4].

Besides the weak gravity conjecture, the swampland approach has led to conjectures about the maximum number of low-mass particles allowed [5], which agrees well with the fact that the standard model has just a handful of fundamental particles. Another conjecture—called the swampland distance conjecture—concerns what happens when one of the compactified dimensions begins to change in extreme ways, such as grow in size. For example, the diameter of a curled-up dimension could become larger, allowing several low-mass particles in this dimension to populate our Universe [6]. This set of new particles, referred to as a “tower of light states,” could have implications in several situations. For example, if such a tower of light states existed in the very early Universe, it would impact inflation—a predicted epoch of exponential expansion at the very beginning of cosmic time. The swampland distance conjecture, therefore, could place interesting constraints on inflation models [7].

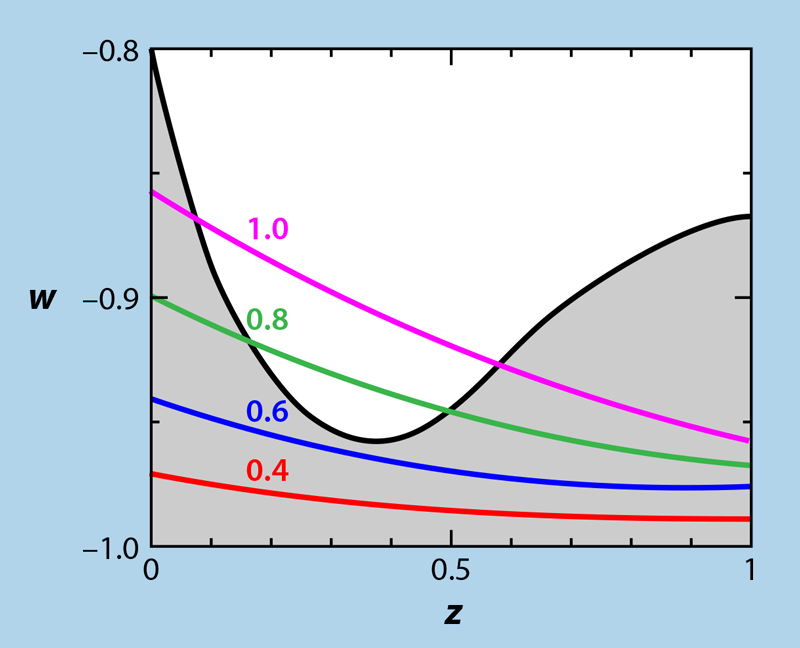
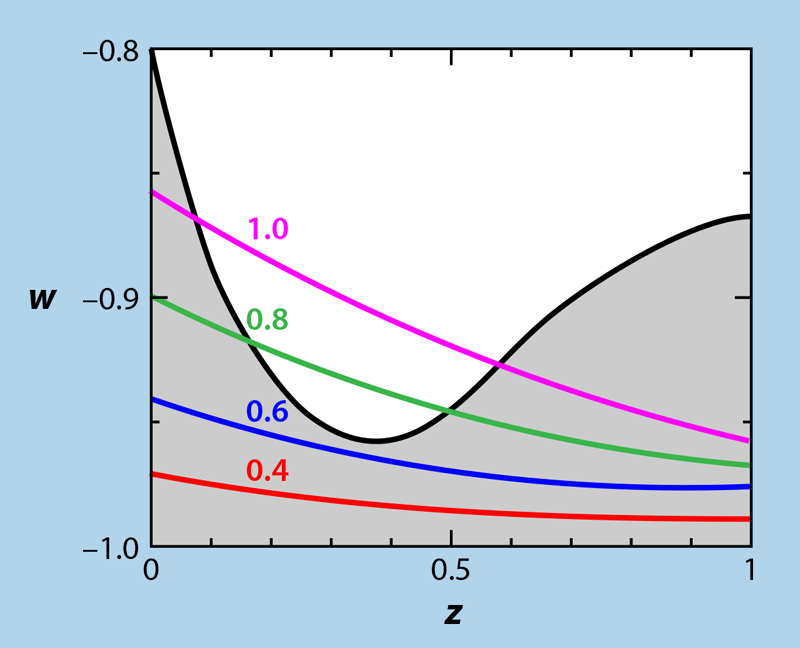
More recently, researchers have proposed additional swampland criteria in response to difficulties in explaining dark energy within string theory [8, 9]. These conjectures are still being debated among string theorists, but if they are true, they lead to predictions about the cosmic expansion history that may be tested in the near future [7, 10]. The conjectures relate to models of dark energy that involve a scalar field $𝜑$, which can be thought of as something like the Higgs field. The field $𝜑$ can be the source of dark energy, in the sense that the field’s potential $V\left(𝜑\right)$ is equal to the density of dark energy $\Lambda$. String theory calculations have suggested that the slope of this potential, $V^{\prime }$, must be nonzero. Specifically, the slope should satisfy the inequality $\left|V^{\prime }\right|>\frac{cV}{M_P}>0$, where c is a number of order unity, at least for large values of the field.

If the above inequality is correct, it implies that dark energy is not a cosmological constant as many cosmologists assume. The alternative to a cosmological constant is a dark energy that is changing over time. Current observational constraints are consistent with this model of dark energy as long as c < 0.5, and future observations of the variation of dark energy can potentially detect or put further bounds on c (Fig. 3).

APS/Alan Stonebraker adapted from [7]

APS/Alan Stonebraker adapted from [7]

×

The swampland conjectures for dark energy may help with fine-tuning problems in cosmology. First, there is the smallness of dark energy, which is miniscule compared to the Planck scale: $\Lambda \sim 10^{-122}{M}_P^4$. The reason for this smallness may be the exponential nature of dark energy swampland conjecture, $V\prime =𝜆V\to V=\Lambda \sim e^{𝜆𝜑}$, which could presumably have driven dark energy density to low values.

A related puzzle is the so-called coincidence problem, which in one version is the observation that the age of the Universe (roughly 14 billion years) is very close to the natural timescale associated with dark energy: ${𝜏}_{\Lambda }=\frac{M_P}{\sqrt{\Lambda }}\approx$ 10 billion years. The swampland conjectures offer an explanation, in that they predict that the Universe will end as we know it, either because the field $𝜑$ tunnels into a new state or because all the matter converts into a tower of light states. In either case, the predicted lifetime for the Universe is less than a few trillion years, which means an observer would have to measure the age of the Universe to be less than $100\times {𝜏}_{\Lambda }$. If this argument holds, it would no longer seem to be such a coincidence that we measure an age of around ${𝜏}_{\Lambda }$.

The swampland distance conjecture combined with the above arguments about dark energy could help us understand the Higgs mass. As the scalar field $𝜑$ evolves, or “rolls” down its potential, a tower of light states should emerge. The masses of these light states—according to various arguments—would be roughly equal to the mass scale corresponding to that of dark energy, which is given by ${\Lambda }^{1∕4}\sim 10^{-3}$ $\text{eV}∕c^2$. This mass value happens to be close to the estimated mass of the neutrinos, $m_{𝜈}$. This may not be a coincidence, as the tower of light states may have a connection to the neutrinos, as well as the Higgs boson. The masses of these particles could be related through a well-known particle physics mechanism called “the seesaw mechanism,” which would result in the Higgs mass not taking the expected value $M_P$ of but instead assuming an intermediate value: $M_H=\sqrt{m_{𝜈}{M}_P}$. Even though these are by no means robust predictions, they point to a potential way that fine-tuning issues of the standard model may be addressed in the context of the string swampland program.

If the swampland conjecture for dark energy is correct, it would lead to the prediction that the standard model of cosmology, the Lambda cold dark matter ( $\Lambda \text{CDM}$), where dark energy is constant, cannot be correct. Quite independently of swampland considerations there have been cosmic controversies brewing over recent experimental observations: Local measurements of the Hubble constant $H_0$ disagree with predictions from $\Lambda \text{CDM}$ based on data from the cosmic microwave background [11]. Either there are systematic errors in the local measurements or $\Lambda \text{CDM}$ is not the correct model. The latter option fits with the swampland ideas. Indeed, the tower of light states that emerge from the rolling of $𝜑$ would constitute a portion of the dark matter, and the way in which these particles evolve over time could help to reduce (though not fully eliminate) the $H_0$ tension [10].

Several upcoming observational probes, such as the Dark Energy Spectroscopic Instrument (DESI) and the Euclid satellite, will give us a better picture of dark energy and dark matter, as well as the value of the Hubble constant. In the next 5–10 years, we may know, for example, whether dark energy is constant or not. If it is, that could pose a serious blow to string theory. But if dark energy is found to be changing, could that observation be the first experimental evidence for ideas emanating from string theory? Only time will tell, but at any rate we seem to be living in interesting times!