Bilayer Graphene’s Wicked, Twisted Road

Overlay two mesh screens, and a panoply of beautiful interference patterns will appear as you rotate one screen with respect to the other (Fig. 1). These “moiré patterns” have long entertained artists, who use the visual effect to create shape and texture. They have also been valuable to scientists, who, for example, exploited the patterns in the 1950s to image defects in crystalline metals [1]. More recently, researchers have discovered fascinating new physics when they create moiré patterns from two or more atomically-thin sheets of atoms. The trick is to delicately peel these sheets from a crystal with loosely bonded atomic layers (a van der Waals crystal) and restack them with a specified relative angle. The resulting “moiré material” often has new electronic and optical properties

APS/Alan Stonebraker

APS/Alan Stonebraker

×

In 2018, this research thread delivered a breakthrough. Working with a double layer of graphene, a team at the Massachusetts Institute of Technology (MIT), Cambridge, discovered that a small relative twist between the layers induced insulating and superconducting states that were completely absent in a single graphene sheet [2, 3]. These phases are tantalizingly similar to those seen in copper-oxide-based (cuprate) high-temperature (high- $T_c$) superconductors. If this similarity indicates that the two materials are fundamentally related, twisted bilayer graphene (TBG), which is a clean and highly tunable system, might serve as a proxy for understanding the enigmatic cuprates. Independent of the possible cuprate connection, TBG is an interesting quantum material in its own right since it provides experimental access to a rich variety of strongly correlated electron phenomena. Written roughly one year after the MIT team’s discovery, this article explores the recent developments of “graphene twistronics” and the big questions driving this fast-growing field forward.

The most interesting quantum materials are often those in which the motion of a given electron depends on that of all the electrons in its surroundings. This “strong correlation” can, for instance, yield unconventional forms of superconductivity and exotic magnetic properties. Strong correlations are favored when electrons move slowly and occupy densely packed energy levels, or “flat bands,” with energies that vary weakly with electron momentum. The energy bands of a crystal are a kind of quantum fingerprint describing how the crystal’s electrons will behave.

The bands of a single graphene sheet are anything but flat. Instead, the band energies depend linearly on momentum—the same dispersion that describes massless relativistic fermions (Dirac fermions.) These so-called Dirac bands are responsible for many of graphene’s interesting properties. But roughly a decade ago, theorists realized that stacking two graphene sheets on top of each other and creating a small relative twist between them would lead to the emergence of a set of “moiré bands.” These bands arise because the twist modulates the electron tunneling between the two layers in a spatially periodic way. For a small twist of a degree or so, the modulation wavelength is extremely long, encompassing thousands of atoms. In these early studies, theorists found that, for small twist angle, the moiré bands become increasingly flat with twist angle [4–6], though the mechanism for band flattening wasn't completely clear. Later studies determined that the twist angle dependence is not monotonic [7–10]: the band width goes up and down with twist angle, vanishing completely at a series of discrete “magic” angles [8], the largest of which is slightly over 1°. These predictions promised that, with a small twist, one could generate flat bands—and therefore strong correlations—on demand. Moreover, they indicated that the strongly correlated electrons would be easy to control. That’s because each magic-angle flat band would contain only about $10^{12}$ electrons per square centimeter. At this level of dilution, experimentalists could, for the first time, use electronic gates to meaningfully tune the electron density in a correlated flat-band material, avoiding disruptive effects of chemical doping like structural distortion. But, as for all good things, one had to wait—in this case for experimentalists to learn to fabricate gated bilayer devices with accurately controlled twist angles.

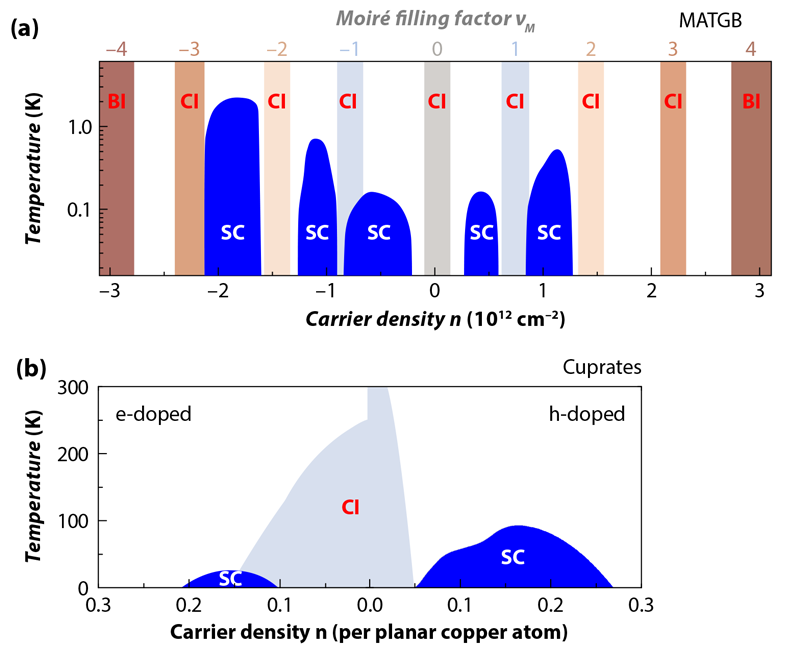
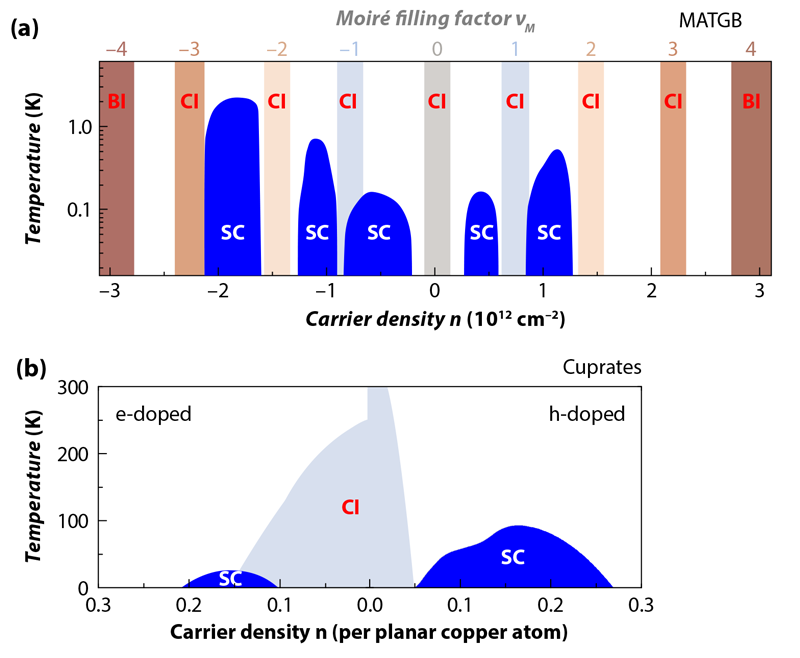
The first graphene moiré superlattices to be carefully studied were “found art,” discovered in graphene flakes grown by chemical vapor deposition [11]. Weakly coupled layers showed some signatures of band flattening within otherwise broad electron bands, and those signatures became amplified at small twist angles [11–14]. In 2013, the MIT team and groups at Columbia University, New York, and the University of Manchester in the UK independently reported that an external magnetic field induced fractal-like distortions in the moiré bands formed by overlaying a single graphene layer on a hexagonal boron nitride substrate [15–17]. The presence of this so-called Hofstadter butterfly showed that moiré patterns could be perfect, or at least nearly so. Eventually experimenters managed to zero in on a magic-angle target in graphene bilayers [18–21]. Quelle surprise! In a striking display of the power of science to astonish and delight, electrons in magic-angle TBG (MATBG) replicated many fascinating properties of the cuprate superconductors, but with their own wicked twists. Examining MATBG at various temperatures and electron densities, the MIT team observed a zoo of phases associated with strongly correlated electrons. Some are Mott insulators [2], in which the electrons, by virtue of strong repulsive interactions, form a gridlock that stops their motion. The insulating states are in close proximity to superconducting phases [3], a situation also seen in the cuprates (Fig. 2). This connection, however, appears to be only the tip of the iceberg of what makes MATBG interesting. This material’s insulating states also exhibit a new form of magnetism, and MATBG’s phase diagram contains many distinct regions of superconductivity.

APS/Alan Stonebraker

APS/Alan Stonebraker

×

In the last year, other experimental groups have not only confirmed the MIT team’s findings but have also made progress toward mapping out the full phase diagram of TBG as a function of twist angle, carrier-density, magnetic-field, pressure, and gate electric field [22–25]. Theorists continue to fuel this exploration with new ideas and predictions. The activity has kicked up some exciting findings, as well as some puzzles.

Do superconductivity and insulating behavior in MATBG have the same physical origin? That’s a key question for researchers to address. At the microscopic level, superconductivity occurs when electrons pair, and the pairs form a single, coherent quantum state. In most simple metals, the pairing is between weakly interacting band electrons. In this picture, any tendency of the electrons to form an insulating phase would suppress superconductivity because fewer electrons would be available to pair. But there is a more exotic possibility, where superconductivity and insulating behavior are “friends.” Here, the pairing occurs between heavily interacting quasiparticles, which move in a correlated-electron environment that locally favors an insulating state. This scenario might, in some systems, like the cuprates, allow superconductivity at much higher temperatures. The idea, however, is not well understood, and there is much hope that we will learn something new and meaningful about it from MATBG.

Whether this hope will be realized in MATBG depends on the relationship between superconductivity and insulating behavior. So far, researchers have determined at least one connection, which is that the two phenomena depend mainly on the same parameter, the moiré filling factor, ${𝜈}_M$. This parameter defines the fraction of filled states in a given band, and it can be tuned with an electronic gate. Such tuning experiments have observed that insulating states occur at most integer values of ${𝜈}_M$, whereas superconductivity frequently occurs when ${𝜈}_M$ is close to, but not equal to, an integer. As a function of experimentally controllable parameters, like twist angle, gate voltage, and pressure, the two phenomena seem to come and go together like pencil and paper (Fig. 2). Establishing that the two phases live and die together would provide a powerful clue that they are related, whereas showing that the two states' existence is only loosely tied together may be a sign that they compete. In this “competing” world, the insulating phase would almost certainly be driven by Coulomb interactions between electrons, while superconductivity could arise mainly from conventional phonon-mediated pairing. Conventional pairing is a realistic possibility; after all, superconductivity is common in graphene-based systems with a high density of states at the Fermi level, such as intercalated graphite. What makes MATBG special in this scenario is simply that it has flat bands, which yield very high densities of states at a very low carrier density.

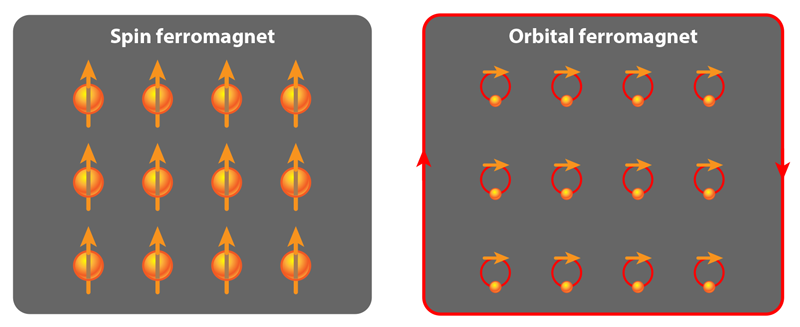
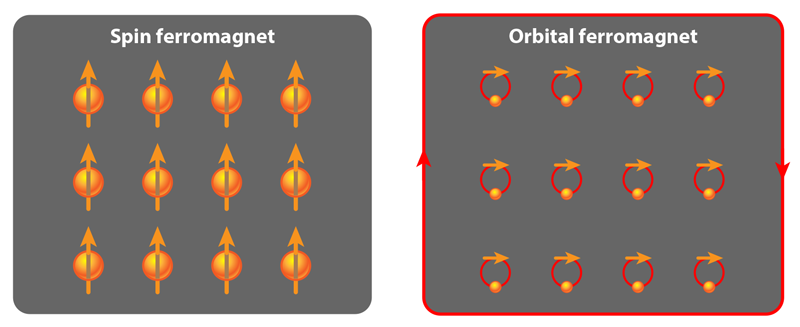
While superconductivity in MATBG was a major surprise, the insulating states may prove to harbor even more exotic physics. Groups at Stanford and the Barcelona Institute of Science and Technology have now shown that some insulating states exhibit ferromagnetism [23, 25]. The main experimental signature that this phase exists is a Hall effect that occurs in the absence of an external magnetic field (anomalous Hall effect) [23]. Another piece of evidence is that the Hall effect is hysteretic, meaning it persists when a magnetic field is turned off [23]. Ferromagnetic behavior is unprecedented in a pure carbon-based system like graphene. Typically, bulk magnetism has a spin part that arises from the alignment of magnetic atoms and an orbital part that is induced by spin-orbit coupling. Since graphene contains no magnetic atoms and has extremely weak spin-orbit coupling, we wouldn’t expect it to display any form of magnetism. Yet MATBG seems to be the first example of bulk magnetism that is purely orbital, as illustrated in Fig. 3.

The fact that insulating MATBG has any Hall signal is already a surprise because the Hall effect requires mobile electrons. The observed Hall signal thus suggests the presence of conducting states that are not in the bulk of MATBG but, instead, on its edge—a hint that TBG has the properties of yet another intriguing system: a topological material called a Chern insulator [26]. In Chern insulators, insulating behavior is peaked at electron densities that depend on magnetic field, a property that is now clearly established [25]. According to the theory of topological materials [26], the anomalous Hall conductivity of an insulator must be quantized, having values corresponding to an integer multiple of $e^2∕h$. This quantization has not yet been observed in MATBG but it’s reasonable to expect that it could soon be. Since MATBG is so clean, it could emerge as the ideal system for experimental studies of this fundamental effect.

APS/Alan Stonebraker

APS/Alan Stonebraker

×

Why does graphene have magic-angle flat bands in the first place? Answering this question is not so simple. The flat bands were first discovered numerically—in one case by performing atomistic model calculations [7], in another by deriving and exploring a low-energy continuum model [8]. The continuum-model approach made one thing clear: the shape of the moiré energy bands depends mainly on a single parameter, the ratio of the interlayer coupling strength to the twist angle [22]. Theoretical work by a team at Harvard University recently found that perfectly flat bands occur at a discrete set of twist angles in a modified continuum model that neglects tunneling between like honeycomb sublattices [27]. This insight suggests that the Dirac bands of single-layer graphene play an essential role in establishing magic-angle behavior, which would therefore be limited to multilayer Dirac systems. Fortunately, even this limited class of system would provide much to explore.

Studies so far have confirmed one prediction over and over again: the electronic properties of TBG are extraordinarily sensitive to twist angle. Reproducibility demands exceptional twist angle control. This is a challenge because the bilayer typically settles into a twist angle that is slightly different from the experimental target. The twist angle can also be different in different parts of a bilayer flake, which induces spatial variations of physical properties. This inhomogeneity makes it hard to interpret transport measurements because the electrons sense a range of twist angles as they propagate in a flake. According to theory, electronic properties change qualitatively when the twist angle is altered by as little as 0.1°. Accurate phase diagrams will therefore require still finer control of twist angle and homogeneity across samples than has been achieved to date. Researchers are, however, making headway in overcoming this obstacle [25], which will allow the twisted multilayer graphene family of strongly correlated electron systems to be fully explored.

The same experimental techniques that enable twisted bilayers provide a way to construct more complex multilayer systems. One interesting possibility is the twisted double-bilayer. This four-layer system [28–30] has a relative twist between two untwisted bilayers, and it is expected to have flat bands whose properties depend on an even wider range of tunable variables compared with simple TBG. Another option is to place a graphene multilayer system on a hexagonal boron nitride substrate, which modifies the multilayer’s properties [31, 32]. In the presence of a gate electric field, these multilayer systems are often gapped semiconductors and mimic the twisted bilayers of another 2D material, transition metal dichalcogenides. Experiments have already shown that the two systems—while qualitatively different—host similar interaction-induced insulating states and, perhaps, similar superconducting states [33]. The multilayer option opens up opportunities to change the twist angles at which flat bands occur, and to make systems in which flat and wide bands appear simultaneously. Such devices might be used to increase the superconducting $T_c$, or to help sort out the relationship between band structure and strong correlation in this class of materials.

The great hope of MATBG research, either boldly declared or modestly unspoken, is that it will teach us something important and general about superconductivity in strongly correlated electron systems. Better yet, this new understanding might help guide the search for new superconductors with record high $T_c$’s. On this front, theory is full of interesting ideas and TBG provides a clean and highly tunable platform for testing them. As for the insulating states, these appear to provide the first experimental example of orbital ferromagnetism, and once better twist angle control is achieved, MATBG could become a factory for Chern insulators and even for fractional Chern insulators. In terms of experiments, probes that microscopically image the electronic bands and track their evolution across the phase diagram of MATBG will be key. Scanning tunneling microscopy and other scanning probes are already providing valuable insights, revealing, for instance, the local effect of the correlations on each flat band [34–36]. New facilities for angle-resolved photoemission spectroscopy (ARPES) on the nanoscale will soon allow researchers to examine the electronic structure of MATBG with greater precision. We are now just beginning. The twisted graphene highway is likely to be full of wicked surprises for correlated-electron physicists. So let's hit the road.