Homing in on the Neutrino Mass
The neutrino remains a truly mysterious particle, despite intense scientific efforts that have lasted for many decades. Even its most basic property—its mass—is still unknown. Understanding what gives the neutrino a mass could help scientists pinpoint new physics beyond the standard model. And since neutrinos are the most abundant massive particles in the Universe, the value of their mass would be important for cosmological models, influencing the formation of large-scale cosmic structures. After almost two decades of planning and preparation, the Karlsruhe Tritium Neutrino (KATRIN) Collaboration in Germany announces its first results [1]. Based on just one month’s worth of data, the Collaboration puts an upper limit of 1.1 eV on the neutrino mass, improving by a factor of 2 the mass limits derived by previous measurements that directly characterized the particle mass.
Since 1998, we have known that the neutrino is massive, in contradiction with the assumptions of the standard model of particle physics. The smoking gun for neutrino mass is evidence of neutrino oscillations, in which one of the three flavors of neutrino transforms into another as it propagates [2–4]. These oscillations are only possible if neutrinos are massive, and the oscillation rate depends on the squared mass difference between the different neutrino mass states: Δm2ij=m2i−m2j, where i,j=1,2,3. The best tools for characterizing these mass differences have been experiments in which flavor oscillations are detected as neutrinos travel over large distances. Such measurements have determined that at least two of the three neutrino masses are larger than about 8×10−3eV. However, completely different strategies must be deployed to gather information on the absolute values, mi, of the neutrino mass states.
Three methods are presently used to constrain the neutrino mass. The first relies on cosmic microwave background (CMB) data [5] to place a constraint on the sum of the three neutrino masses. The second method is based on searching for neutrinoless double-beta decay [6]—a radioactive decay process in which two neutrons decay into two protons and two electrons without emitting neutrinos. This decay is extremely rare and has never been seen in experiments. This nondetection, however, places limits on the decay rate, which, in turn, constrains the effective Majorana mass m𝛽𝛽—a linear combination of the neutrino masses weighted by factors, U2ei, related to neutrino mixing: m𝛽𝛽=|ΣU2eimi|. Experiments of this type have obtained very good sensitivity on the sum and effective Majorana masses and hold promise for significant improvements in the future. However, the constraints derived from these methods depend on the cosmological and double-beta-decay models used to fit the data.
The third method, on which KATRIN relies, provides a direct measurement of the neutrino mass that doesn’t depend on an underlying model. This method, known as beta-decay end point, is based on observing the beta decay of tritium into helium-3, an electron, and an electron antineutrino. The end point is the maximum energy of the emitted electron. Compared to the massless neutrino case, the end point value is shifted by the neutrino mass ( m𝛽=√U2eim2i) and the shape of the energy distribution of the emitted electron is distorted. The challenge for experiments is that the relevant information is contained at the high-energy end of the emitted-electron spectrum, where the electron count rate is dropping rapidly. To reach the sensitivity needed to resolve these tiny effects, experiments need a source that produces a large rate of beta decays, a detector with high-energy resolution and high efficiency, and an environment producing a low rate of background events.
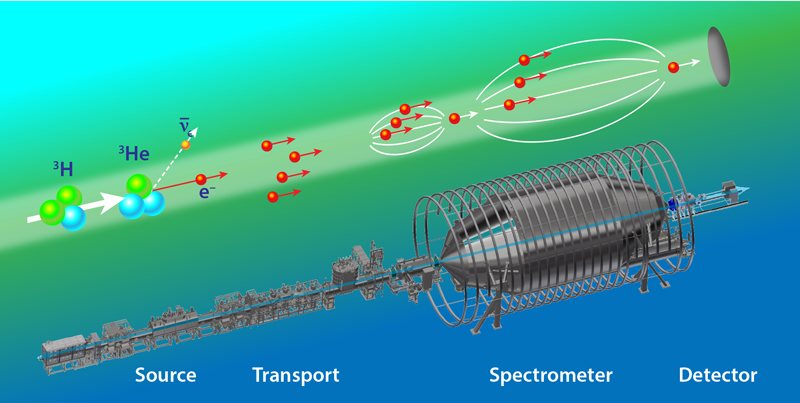
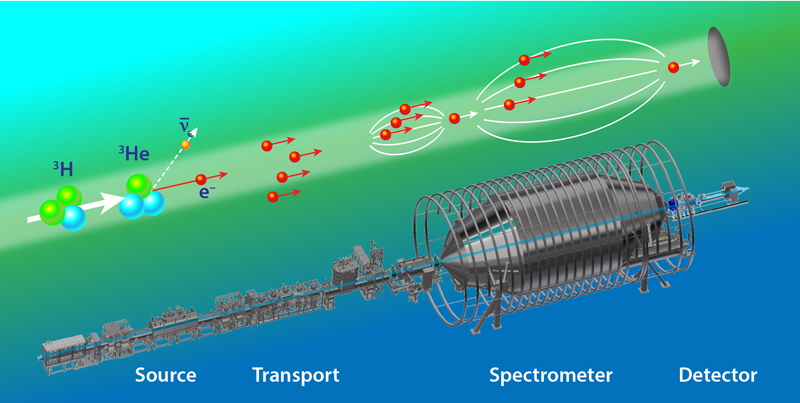
After a long R&D program, KATRIN managed to fulfil all these requirements by adopting and optimizing all the best technologies developed in past years. In particular, a gaseous source provided a strong flow of molecular tritium with high isotopic purity. And a giant spectrometer (Fig. 1) based on magnetic collimation in combination with electrostatic filtering allowed the researchers to select only electrons near the end point energy of 18.57 keV and measure their energy with an energy resolution of 2.8 eV. Thanks to these features, the scheme (Fig. 2) allowed the collaboration to characterize the end point region with large signal-to-noise ratio and small systematic errors. Remarkably, with just four weeks of data taking, the total statistical uncertainties were a factor of 2 better than any previous experiment. KATRIN obtained an upper limit on the neutrino mass of 1.1 eV (at 90% confidence level)—about 2 times smaller than that derived by previous model-independent characterizations based on isotope decay.
What will happen in the future? KATRIN will take data for five more years in order to reach its final sensitivity of 0.2 eV. Beyond that point, no improvements can be easily envisaged, as KATRIN has reached the maximum size and complexity practically achievable. If the neutrino’s mass doesn’t appear at 0.2-eV sensitivity, KATRIN won’t be likely to help scientists further.
Alternative ways have to be explored to go beyond KATRIN. Project 8 proposes a new experimental approach based on the detection of the cyclotron radiation emitted by electrons [7]. Like KATRIN, Project 8 is based on the tritium beta-decay end point, but the idea is to measure the energy of the emitted electrons by placing them in a circular orbit and detecting the radiation they produce. The experiment is expected to reach a sensitivity of 40 meV in its final stage. Another possibility for a direct neutrino-mass measurement is provided by the study of electron capture in the artificial isotope holmium-163. Two projects, ECHo [8] and HOLMES [9], aim to measure the energy released in the decay of holmium-163 following electron capture. A careful accounting should reveal some missing energy that will depend on the mass of the neutrino. Both experiments are designed to reach sub-eV sensitivity on the mass of electron neutrinos. Finally, the PTOLEMY project follows a different approach [10], aimed at detecting the cosmic neutrino background (CNB)—relic neutrinos released during the big bang. While the CNB has not yet been observed, there is indirect evidence that it exists. PTOLEMY involves capturing CNB neutrinos in tritium nuclei and characterizing their mass with a technique that combines KATRIN’s spectrometry approach with Project 8’s cyclotron radiation approach.
With so many new interesting measurements around the corner, one of the most pressing questions in physics may find an answer sooner than we think.
This research is published in Physical Review Letters.
References
- M. Aker et al. (KATRIN Collaboration), “Improved upper limit on the neutrino mass from a direct kinematic method by KATRIN,” Phys. Rev. Lett. 123, 221802 (2019).
- Y. Fukuda et al. (Super-Kamiokande Collaboration), “Evidence for Oscillation of Atmospheric Neutrinos,” Phys. Rev. Lett. 81, 1562 (1998).
- Q. R. Ahmad et al. (SNO Collaboration), “Direct evidence for neutrino flavor transformation from neutral-current interactions in the Sudbury Neutrino Observatory,” Phys. Rev. Lett. 89, 011301 (2002).
- K. Eguchi et al. (KamLAND Collaboration), “First Results from KamLAND: Evidence for reactor antineutrino disappearance,” Phys. Rev. Lett. 90, 021802 (2003).
- N. Aghanim et al. (Planck Collaboration), “Planck 2018 results. VI. Cosmological parameters,” arXiv:1807.06209 .
- M. Agostini et al. (GERDA Collaboration), “Probing Majorana neutrinos with double-𝛽 decay,” Science 365, 1445 (2019).
- A. Ashtari Esfahani et al. (Project 8 Collaboration), “Determining the neutrino mass with cyclotron radiation emission spectroscopy—Project 8,” J. Phys. G 44, 054004 (2017).
- L. Gastaldo et al., “The electron capture in 163Ho experiment – ECHo,” Eur. Phys. J. Spec. Top. 226, 1623 (2017).
- A. Nucciotti et al., “The use of low temperature detectors for direct measurements of the mass of the electron neutrino,” Adv. High Energy Phys. 2016, 9153024 (2016).
- M. G. Betti et al., “Neutrino physics with the PTOLEMY project: active neutrino properties and the light sterile case,” J. Cosmol. Astropart. Phys. 7, 047 (2019).