A Unifying Framework for Describing Rogue Waves
In oceanography, rogue or freak waves (Fig. 1) are defined as waves that are abnormally large compared with the average waves for a given sea state [1]. With heights exceeding 30 meters, these statistically rare waves pose severe threats even to the largest ships. Unlike tsunamis caused by earthquakes, rogue waves are, so far, unpredictable and localized in space and time—they are often said “to appear from nowhere and disappear without a trace” [2]. Understanding the mechanisms of their formation would be essential to develop tools for predicting their occurrence. However, such mechanisms remain disputed, with two competing schools of thought: one arguing that their origin is due to linear interference [3], the other saying that nonlinear phenomena are the key [4]. Now, Giovanni Dematteis from the Polytechnical University of Turin in Italy and co-workers have shown that a theory for rogue waves based on mathematical entities known as instantons successfully describes controlled experiments performed in a large-scale water tank [5]. The instanton theory, which can tackle regimes of propagation ranging from nearly linear to fully nonlinear, could pave the way for a universal description of rogue waves that is applicable to many real-world situations.
The reliable recording of rogue waves, starting from the well-known Draupner wave observed in 1995 around a North Sea oil platform [6], brought these waves out of a mythical status, turning them into a fascinating area of rigorous experimental and theoretical research. Work performed in the last two decades suggested that rogue waves are ubiquitous phenomena with clear manifestations in optics, plasmas, economics, and climatology [7]. Water waves and optics, in particular, have offered the possibility to investigate rogue waves in the lab by performing experiments that are controllable but also able to simulate the random nature of wave superposition that is at the basis of rogue wave formation.
In spite of significant theoretical, numerical, and experimental progress, there is no consensus on how rogue waves form. Researchers in the linear camp attribute rogue wave events to constructive interference between waves, which can accidentally pile up at some location. Conversely, supporters of a nonlinear origin argue that rogue waves could be produced by mechanisms that amplify and focus long-wavelength fluctuations [8, 9]. These nonlinear effects can lead to so-called Peregrine solitons, or breathers, which are waves characterized by an isolated high peak that first grows and then dies out [9]. Some features of Peregrine solitons are consistent with the properties of rogue waves, making them an attractive hypothesis for explaining their formation. However, observations and experiments under a variety of conditions have given conflicting results about whether a linear or a nonlinear description is more accurate.
With the goal of reconciling these two descriptions, Dematteis and his co-workers tackle the dynamics of rogue waves with instanton theory. This theory was originally developed within the framework of quantum chromodynamics (QCD), which describes the strong interactions between quarks and gluons [10]. Instantons are waveforms that can be calculated following an approach based on large-deviation theory, which deals with a quantitative description of how rare events occur. The calculations involve minimizing a certain “action functional” (see note in Ref. [11]). In simple words, instantons are obtained as the most likely trajectories that lead to the realization of an event with little likelihood.
While developed in the very different context of QCD, instanton theory appears to be a powerful and quite natural tool to describe stochastic wave fields in the presence of nonlinearities. In fluids, the theory has been applied to describe particular regimes of turbulence. The researchers previously derived an instanton-based description of waves within the universal nonlinear Schrödinger model, which is often used to characterize wave propagation in deep water. They used this instanton description to estimate the likelihood of the appearance of rogue waves as well as the shape of the waves [12].
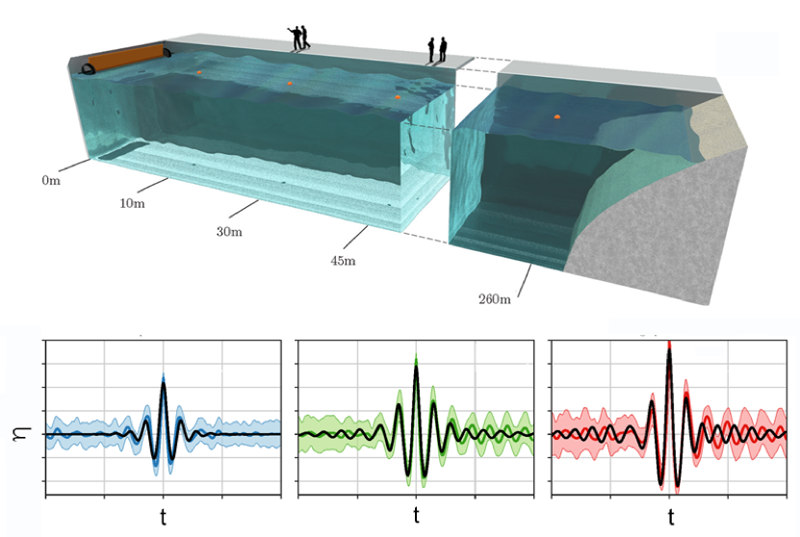
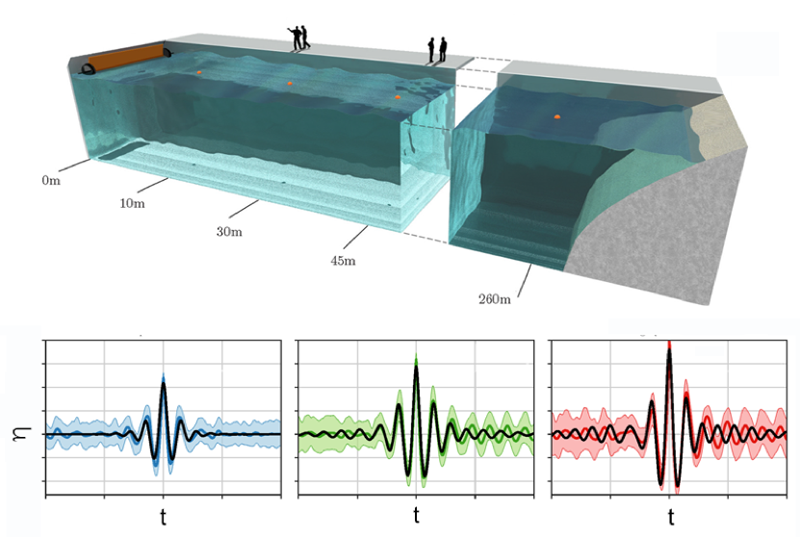
In the new work, the team put their instanton theory to the test in a set of laboratory experiments. In a 270-m-long water tank in Marintek, Norway (Fig. 2, top), they use a wave maker to generate sinusoidal waves with different wavelengths and random phases, mimicking a rough, unidirectional sea. The waves propagate along the tank, where vertical probes measure the water surface elevation as a function of time. A key feature of the setup is that it allows the researchers to tailor the relative impact of linear and nonlinear effects by manipulating the spectra of the input random waves. Occasionally, the setup produces extreme events—waves with amplitudes that exceed the average amplitude by at least five times the standard deviation. This behavior allows the team to identify and characterize a large set of extreme events and their precursors. The main outcome is that the instanton theory bridges the gap between the two descriptions: predictions based on the instanton theory can accurately reproduce the experimental waveforms of rogue waves for regimes where linear or nonlinear effects dominate, as well as for those regimes where both are relevant (Fig. 2, bottom).
Importantly, in the limit of strong nonlinearity, the shape of the rogue wave peak calculated with instanton theory resembles the peak of the famed Peregrine breather [9]. This result shows that their instanton theory encompasses the particular and well-studied cases that are properly described by Peregrine breathers. However, the instanton theory provides a better fit to the tails of the waveforms away from the peak, for which the Peregrine breather picture is known to be inaccurate.
The results suggest that the instanton theory could provide a universal description of rogue wave formation in different regimes and media. Compared to previous approaches, an important advantage of the theory is that it could be applied to more complicated and more realistic ocean configurations, such as sea states in which waves have a spectrum of directions. Obviously, the instanton model would have to be validated by experiments able to probe these configurations. It would also be interesting to explore whether instanton theory can describe higher-order nonlinear waves resulting from the nonlinear superposition of several unstable wave packets. The results by Dematteis et al. will certainly boost research activities aimed at finding ways to predict rogue wave formation, as well as at exploring the universal character of rogue wave dynamics in a wide range of physical systems.
This research is published in Physical Review X.
References
- C. Kharif, E. Pelinovsky, and A. Slunyaev, Rogue waves in the ocean (Springer Science & Business Media, New York, 2008)[Amazon][WorldCat].
- N. Akhmediev, A. Ankiewicz, and M. Taki, “Waves that appear from nowhere and disappear without a trace,” Phys. Lett. A 373, 675 (2009).
- J. Gemmrich and J. Thomson, “Observations of the shape and group dynamics of rogue waves,” Geophys. Res. Lett. 44, 1823 (2017).
- W. Fujimoto, T. Waseda, and A. Webb, “Impact of the four-wave quasi-resonance on freak wave shapes in the ocean,” Ocean Dynam. 69, 101 (2018).
- G. Dematteis, T. Grafke, M. Onorato, and E. Vanden-Eijnden, “Experimental evidence of hydrodynamic instantons: The universal route to rogue waves,” Phys. Rev. X 9, 041057 (2019).
- S. Haver, “A possible freak wave event measured at the draupner jacket January 1 1995,” in Proceedings of Rogue Waves 2004, edited by M. Olagnon and M. Prevosto (Ifremer, Brest, 2005), p. 1–8[Amazon][WorldCat].
- M. Onorato, S. Residori, U. Bortolozzo, A. Montina, and F. T. Arecchi, “Rogue waves and their generating mechanisms in different physical contexts,” Phys. Rep. 528, 47 (2013); J. M. Dudley, G. Genty, A. Mussot, A. Chabchoub, and F. Dias, “Rogue waves and analogies in optics and oceanography,” Nat. Rev. Phys. 1, 675 (2019).
- T. B. Benjamin and J. E. Feir, “The disintegration of wave trains on deep water Part 1. Theory,” J. Fluid Mech. 27, 417 (1967).
- D. H. Peregrine, “Water waves, nonlinear Schrödinger equations and their solutions,” J. Aust. Math. Soc. Series B. App. Math. 25, 16 (1983).
- A. A. Belavin, A. M. Polyakov, A. S. Schwartz, and Yu. S. Tyupkin, “Pseudoparticle solutions of the Yang-Mills equations,” Phys. Lett. B 59, 85 (1975); T. Schäfer and E. V. Shuryak, “Instantons in QCD,” Rev. Mod. Phys. 70, 323 (1998).
- Technically speaking, the instanton realizes the maximum likelihood pathways—the minimizer of the action functional that gives the constrained probability of the rare event in the space of all possible realizations.
- G. Dematteis, T. Grafke, and E. Vanden-Eijnden, “Rogue waves and large deviations in deep sea,” Proc. Natl. Acad. Sci. 115, 855 (2018); T. Grafke and E. Vanden-Eijnden, “Numerical computation of rare events via large deviation theory,” Chaos 29, 063118 (2019).