A Polka-Dot Pattern Emerges in Superfluid Helium

Jochen Wosnitza

Viewpoint

A Polka-Dot Pattern Emerges in Superfluid Helium

Dresden High Magnetic Field Laboratory (HLD-EMFL), Helmholtz-Zentrum Dresden-Rossendorf, Dresden, Germany
Institute of Solid State and Materials Physics, Technical University Dresden, Dresden, Germany

February 27, 2019• Physics 12, 20

A surprising two-dimensional pattern appears in superfluid helium-3 when the liquid is confined to a micrometer-thick cell and exposed to a magnetic field.

Figure caption — **Figure 1:** (Left) A sketch of the one-dimensional order-parameter modulation in the FFLO state of organic superconductors, where the stripes correspond to different superconducting phases separated by magnetically ordered regions (blue). (Right) The two-dimensional polka-dot pattern proposed by Saunders, Parpia, and colleagues to explain nuclear magnetic resonance observations of superfluid helium-3 [1]. The domains here correspond to different superfluid phases ( $B_{+}$ and $B_{-}$ ), which are separated by nonsuperfluid domain walls (blue).

The occurrence of superconductivity is a common phenomenon in metals. In this zero-resistance state, electrons form a condensate of Cooper pairs that can transport electrical current without dissipation. Such pairing of spin-1/2 particles (fermions) also happens in ultracold gases, neutron stars, quark matter, and neutral helium-3 atoms. In all these cases, the Cooper-pair condensate is very robust against perturbations, and its ground-state density is spatially uniform on macroscopic length scales. However, the Cooper-pair density can become spatially modulated under external constraints. A well-known example of spatial modulation is the formation of vortices in type-II superconductors exposed to a magnetic field. Now, researchers led by John Saunders from Royal Holloway, University of London and Jeevak Parpia from Cornell University, New York, have found evidence for a new type of spatially modulated order in superfluid helium-3 in a confined geometry [1]. Using sophisticated nuclear magnetic resonance (NMR) techniques, the team shows that two phases of the superfluid form separate domains in a polka-dot pattern. Further study of this system may help in locating other spatial patterns in superconductors or superfluids.

In the late 1950s, shortly after the establishment of the groundbreaking microscopic theory of superconductivity by John Bardeen, Leon Cooper, and Robert Schrieffer (BCS), questions arose over the stability of the superconducting state under a strong magnetic field. If the field is above the so-called Pauli limit—where the magnetic potential energy (or Zeeman energy) of the electrons is stronger than the superconducting condensation energy—then the superconducting state may be destroyed by spin-flipping of one of the electrons in a Cooper pair.

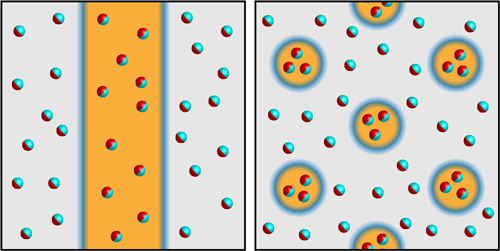
However, even in fields beyond the Pauli limit, it may be possible to conserve superconductivity in certain regions of the material. In 1964, Peter Fulde and Richard Ferrell as well as Anatoly Larkin and Yuri Ovchinnikov independently predicted that such a spatially modulated superconducting state may emerge at high fields and low temperatures [2, 3]. This “compromise” state, now called the FFLO state, arises from the energy imbalance between spin-up and spin-down electrons in the strong magnetic field. At fields beyond the Pauli limit, the usual BCS pairing of electrons with equal and opposite momentum is no longer possible and, instead, Cooper pairing may occur with a net momentum that is nonzero. This results in an oscillation of both the superconducting order parameter (Cooper-pair density) and the spin density, which manifests itself as stripes of superconducting phase separated by magnetically ordered domain walls (Fig. 1).

For FFLO states to occur, special conditions have to be fulfilled. The superconductor must, for example, contain very few impurities, so that the Cooper pairs have a mean-free path that is much longer than their coherence length. This restricts the number of candidate materials that may show FFLO states. In 2007, researchers found the first firm experimental evidence for FFLO states in layered organic superconductors [4]. The experiments, which came more than four decades after the initial prediction, used specific-heat and later NMR measurements to identify a 1D modulation of the spin density in the superconductors [5, 6].

Besides simple 1D spatial oscillations, theories predict that FFLO states with 2D or 3D periodic patterns can occur [7, 8]. But until now, no such higher dimensional patterns have been observed. In a joint effort, the Royal Holloway and Cornell groups have uncovered 2D spatial modulations of the superfluid order parameter in a helium-3 system [1]. They studied helium-3 at low pressures and at temperatures below 1 mK, where the helium-3 atoms pair up in a $p$ -wave, spin-triplet state—the so-called $B$ phase. For confined geometry in a magnetic field, this phase can further split into two new phases, called $B_{+}$ and $B_{-}$ , which are identifiable through positive or negative shifts in the resonance frequency of NMR measurements. The stability of these two superfluid phases is strongly influenced by mesoscopic confinement. In previous work, the Royal Holloway and Cornell groups, together with a group in Berlin determined the conditions—related to geometry, magnetic field, and pressure—that lead to the appearance of the different $B$ phases [9].

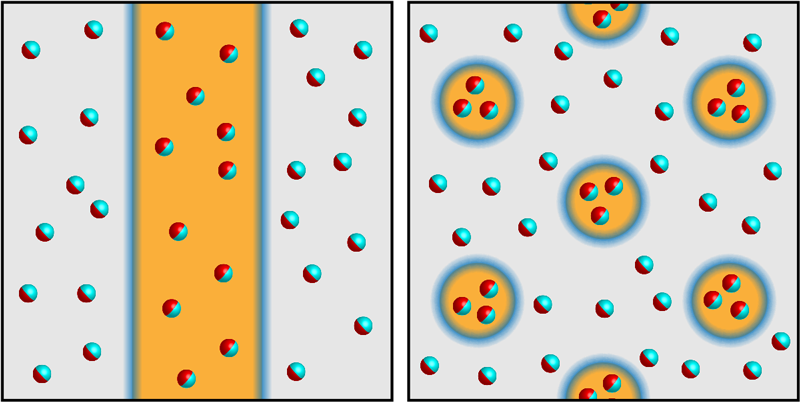
In the present experiment, the authors optimized their mesoscopic confinement in order to observe spatial modulations [1]. They placed helium-3 in a silicon-glass cell with a cavity height of 1.1 $𝜇 m$ . Under a pressure of 30 mbar, they performed pulsed NMR measurements in a magnetic field of 31 mT, applied perpendicularly to the slab. Below about 0.7 mK, the researchers identified the two $B$ phases. The expectation was that the superfluid would exhibit a 1D modulation in which domains of $B_{+}$ and $B_{-}$ would form stripes with nonsuperfluid domain walls in between. Careful analysis of the NMR data, however, showed that under certain conditions the area covered by $B_{+}$ domains was 4 times greater than the area of $B_{-}$ domains, which ruled out the stripe pattern hypothesis. The simplest alternative—given the observed partition of domain areas—is a 2D modulation in the superfluid order, in which the $B_{-}$ domains are like polka dots within an extended $B_{+}$ domain (Fig. 1).

Several questions remain unanswered about this polka-dot pattern. What are the sizes of the polka dots and how far apart are they? Are the boundaries between the phases sharp or gradual? Do other types of order-parameter modulations exist? A real-space imaging of the modulated structures would be desirable, not only for the superfluid phase in confined helium-3 but also for modulated FFLO-like states in general. Future studies on condensed-matter model systems are expected to shed more light on some of the unsolved questions.

As the polka-dot pattern was not expected, new theoretical work will be needed to uncover its origin. A better understanding of constricted helium-3’s behavior may give insight into ways of initiating similar 2D modulations in other systems, such as ultracold gases or superconductors. In general, spatially modulated FFLO-like states, which break translational invariance, are expected to occur whenever there is a population imbalance (between spin-up and spin-down states, for example). The advantage of investigating these modulations in helium-3 is that it is a very clean model system. So we await further revelation.

This research is published in Physical Review Letters.

References

L. V. Levitin, B. Yager, L. Sumner, B. Cowan, A. J. Casey, J. Saunders, N. Zhelev, R. G. Bennett, and J. M. Parpia, “Evidence for a spatially modulated superfluid phase of $^{3} He$ under confinement,” Phys. Rev. Lett. 122, 085301 (2019).
P. Fulde and R. A. Ferrell, “Superconductivity in a strong spin-exchange field,” Phys. Rev. 135, 550 (1964).
A. I. Larkin and Yu. N. Ovchinnikov, “Inhomogeneous state of superconductors,” Sov. Phys. JETP 20, 762 (1965).
R. Lortz, Y. Wang, A. Demuer, P. H. M. Böttger, B. Bergk, G. Zwicknagl, Y. Nakazawa, and J. Wosnitza, “Calorimetric evidence for a Fulde-Ferrell-Larkin-Ovchinnikov superconducting state in the layered organic superconductor $𝜅 − {(BEDT − TTF)}_{2} Cu {(NCS)}_{2}$ ,” Phys. Rev. Lett. 99, 187002 (2007).
G. Koutroulakis, H. Kühne, J. A. Schlueter, J. Wosnitza, and S. E. Brown, “Microscopic study of the Fulde-Ferrell-Larkin-Ovchinnikov state in an all-organic superconductor,” Phys. Rev. Lett. 116, 067003 (2016).
J. Wosnitza, “FFLO states in layered organic superconductors,” Ann. Phys. 530, 1700282 (2018).
Y. Matsuda and H. Shimahara, “Fulde-Ferrell-Larkin-Ovchinnikov state in heavy fermion superconductors,” J. Phys. Soc. Jpn. 76, 051005 (2007).
G. Zwicknagl and J. Wosnitza, “Breaking translational invariance by population imbalance: The Fulde-Ferrell-Larkin-Ovchinnikov states,” in BCS: 50 years, edited by L. N. Cooper and D. Feldman (World Scientific, Singapore, 2011), p. 337[Amazon][WorldCat].
L. V. Levitin, R. G. Bennett, A. Casey, B. Cowan, J. Saunders, D. Drung, Th. Schurig, and J. M. Parpia, “Phase diagram of the topological superfluid 3He confined in a nanoscale slab geometry,” Science 340, 841 (2013).

About the Author

Jochen Wosnitza studied physics at RWTH Aachen University and received his Ph.D. in 1988 from the University of Karlsruhe (now KIT). After a postdoctoral stay at Argonne National Laboratory, he returned to Karlsruhe in 1995. He became a professor at the Technical University Dresden in 2001. Since 2004, he has also been director of the Dresden High Magnetic Field Laboratory (HLD) at the Helmholtz-Zentrum Dresden-Rossendorf. His research interest focuses on strongly correlated electron systems, especially unconventional superconductivity and frustrated magnetism. In 2011 he was recognized as an Outstanding Referee by the American Physical Society.