Dipolar Quantum Gases go Supersolid
Solids are rigid and liquids flow—a distinction that’s clear in our classical world. But this dichotomy breaks down at low temperatures where quantum effects prevail, allowing for a bizarre form of matter called a supersolid. This material’s atoms have the spatial periodicity of a crystal, yet they flow without friction. Fascinated with this idea, researchers have sought supersolidity for decades, first in helium, where experiments are ongoing, and then in quantum gases, where evidence of supersolidity was found in Bose-Einstein condensates (BECs) of atoms manipulated with light. Now three research teams have identified properties of a supersolid in what has long been considered one of the best places to look for it—BECs of atoms with large magnetic dipole moments [1–3].
The notion of a supersolid began about 50 years ago, when theorists proposed that a collection of cold bosonic particles could both condense into a frictionless “superfluid” and spontaneously acquire a density modulation [4, 5]. Such a modulation would only form if it was favored by the interaction between the atoms. And it would show up as a dip in the energy-momentum spectrum of the superfluid’s excitations. The momentum of this “roton minimum” would correspond to the period of the modulation.
Efforts to create supersolids in the lab have largely started with a superfluid and then tailored the atom interactions to induce crystallization—all while preserving the fragile coherence of the superfluid phase. Early experiments in the 1970s concentrated on superfluid helium-4, the only bosonic quantum liquid available at the time. Helium has a roton minimum. But while a 2004 paper reported signatures of superfluidity in solidified helium, a 2012 follow-up determined the effects had come from other sources [6]. (See 8 October 2012 Focus story.) So far, it seems, helium-4 can only be either a superfluid liquid or a normal crystal.
Around the time of the first helium-4 claims, theorists turned their sights to supersolidity in a new system: a BEC of an atomic gas. At first glance, a density modulation shouldn’t be possible in such a BEC because its atoms are so dilute and have only weak short-range (contact) interactions. But a pair of papers from 2003 proposed a way to engineer the necessary atom interaction in the form of a long-range dipolar coupling [7, 8]. This interaction would induce a roton minimum, similar to that of helium, opening a path to supersolidity. Various methods exist to create dipolar interactions. They can come from induced or permanent electric dipole moments of the particles. Or they can arise from atoms with strong magnetic dipole moments. In 2017, experimentalists followed the spirit of the first course and observed the first evidence for supersolidity in BECs. These groups achieved the necessary atom interactions by coupling the BECs to light fields, either exploiting spin-orbit coupling [9] or cavity-mediated long-range interactions [10] between the atoms.
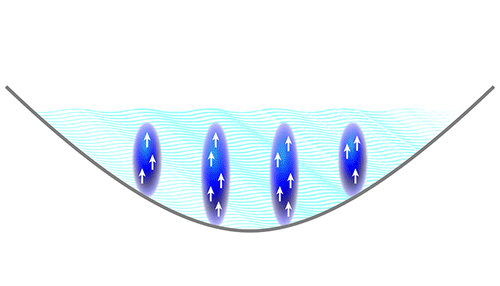
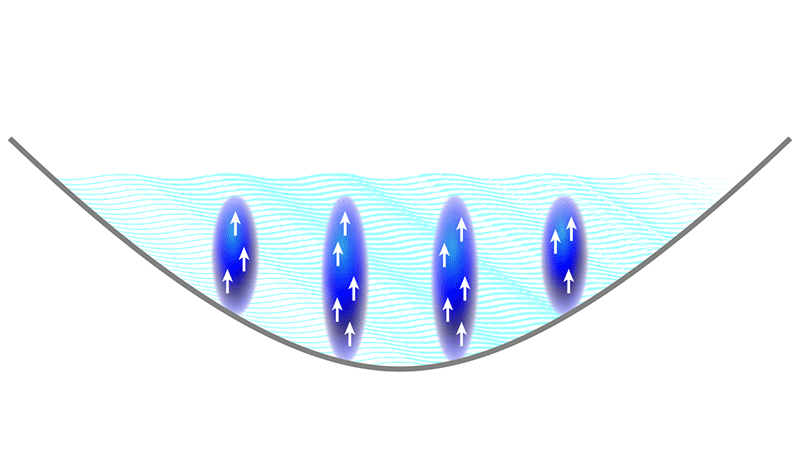
The three new experiments more closely realize one of the original 2003 proposals [8] by making use of the naturally strong magnetic dipole moments in BECs of dysprosium and erbium. For several years, researchers have known these BECs have the ingredients for supersolidity. First, they are superfluids. And second, under certain conditions, the atoms will segregate into several dense droplets, providing the necessary density modulation. To drive this droplet transition, experimentalists must ensure a sufficiently large dipolar interaction between the atoms and subject the gas to an appropriately anisotropic trap. But so far, the droplets created in this way have been too far apart to maintain the phase coherence required for a superfluid. Ideally, droplets achieve mutual coherence through the tunneling of atoms from one droplet to the other. Last year, theorists showed that a regime should exist where the droplets are immersed in a background of Bose-condensed atoms, thereby establishing the required tunneling (Fig. 1). The trick is to choose the correct trapping potential, the right ratio of dipolar-to-contact interaction, and a high enough atom number [11, 12].
All three teams have zeroed in on the narrow window in parameter space that realizes this scenario, and they have demonstrated the mutual phase coherence between the droplets—an indirect indication of superfluidity. The researchers did this by letting the matter waves of the atoms interfere when the entire cloud was released from the trap and allowed to expand. This test is similar to looking for the interference of waves emerging from a regular array of individually coherent point sources: an interference pattern will always appear somewhere, regardless of whether the sources are coherent with one another. But by showing that the interference pattern always occurred at the same point in space for repeat experiments, the three groups could prove mutual coherence of the drops.
The main difference in the three experiments lies in the stability of this supersolid signature. Two of the teams—one led by Giovanni Modugno of the University of Florence, Italy [1], the other by Tilman Pfau of the University of Stuttgart, Germany [2]—used the isotope dysprosium-162 ( ). With this atomic species, the repulsive contact interaction between atoms usually dominates the dipolar interaction. Therefore, in order to reach the regime of droplet formation, the researchers tuned the contact interaction downwards by exploiting a so-called Feshbach resonance between the atoms. But tuning towards this resonance also results in atom loss, limiting the lifetime of the supersolid signatures to tens of milliseconds.
The third team, led by Francesca Ferlaino of the University of Innsbruck, Austria, explored two other isotopes, erbium-166 ( ) and dysprosium-164 ( ) [3]. Erbium suffers from the same loss problems as . But features naturally dominant dipolar interactions. As a result, the team could tune away from a Feshbach resonance and minimize atom losses, allowing for supersolid behavior that lasted for more than 150 ms. They obtained this value by first preparing the BEC and then “dialing in” the necessary experimental parameters. But reversing these steps resulted in an even longer lifetime for the supersolid because excitations generated while preparing the droplet phase could be cooled away.
The trio of experiments demonstrates that dipolar gases can exhibit the properties of a supersolid. The next step would be to study this peculiar phase’s excitations, including its so-called phononic and rotonic modes. Acquiring more direct evidence than droplet coherence that superfluidity is intact would be interesting albeit demanding. It would entail, for example, measuring the transport of the gas through a narrow constriction or exciting vortices when stirring the gas. Also, the teams each achieved only a handful of droplets. But I am curious to see whether dozens or more droplets are possible, which would show that the system size isn’t limited by the specific properties of dipolar gases. With additional experimental and theoretical work, we are certain to learn more about this exciting new arena for supersolid behavior.
This research is published in Physical Review X and Physical Review Letters.
References
- L. Tanzi, E. Lucioni, F. Famà, J. Catani, A. Fioretti, C. Gabbanini, R. N. Bisset, L. Santos, and G. Modugno, “Observation of a dipolar quantum gas with metastable supersolid properties,” Phys. Rev. Lett. 122, 130405 (2019).
- F. Böttcher, J.-N. Schmidt, M. Wenzel, J. Hertkorn, M. Guo, T. Langen, and T. Pfau, “Transient Supersolid Properties in an Array of Dipolar Quantum Droplets,” Phys. Rev. X 9, 011051 (2019).
- L. Chomaz et al., “Long-Lived and transient supersolid behaviors in dipolar quantum gases,” Phys. Rev. X 9, 021012 (2019).
- A. F. Andreev and I. M. Lifshitz, “Quantum theory of defects in crystals,” Sov. Phys. JETP 29, 1107 (1969).
- G. V. Chester, “Speculations on Bose-Einstein condensation and quantum crystals,” Phys. Rev. A 2, 256 (1970).
- D. Y. Kim and M. H. W. Chan, “Absence of supersolidity in solid helium in porous Vycor glass,” Phys. Rev. Lett. 109, 155301 (2012).
- D. H. J. O’Dell, S. Giovanazzi, and G. Kurizki, “Rotons in Gaseous Bose-Einstein condensates irradiated by a laser,” Phys. Rev. Lett. 90, 110402 (2003).
- L. Santos, G. V. Shlyapnikov, and M. Lewenstein, “Roton-maxon spectrum and stability of trapped dipolar Bose-Einstein condensates,” Phys. Rev. Lett. 90, 250403 (2003).
- J.-R. Li, J. Lee, W. Huang, S. Burchesky, B. Shteynas, F. Ç. Top, A. O. Jamison, and W. Ketterle, “A stripe phase with supersolid properties in spin–orbit-coupled Bose–Einstein condensates,” Nature 543, 91 (2017).
- J. Léonard, A. Morales, P. Zupancic, T. Esslinger, and T. Donner, “Supersolid formation in a quantum gas breaking a continuous translational symmetry,” Nature 543, 87 (2017).
- D. Baillie and P. B. Blakie, “Droplet crystal ground states of a dipolar Bose gas,” Phys. Rev. Lett. 121, 195301 (2018).
- S. M. Roccuzzo and F. Ancilotto, “Supersolid behaviour of a dipolar Bose-Einstein condensate confined in a tube,” arXiv:1810.12229.