Revealing the Coherence of Magnons
In 1956, the astrophysicists Robert Hanbury Brown and Richard Twiss discovered a new effect with light. They found that when photons from a coherent light source are split into two beams and directed to different photodetectors, the signals from the detectors are correlated [1]. Later experiments showed that coherent, partially coherent, and incoherent photons display different correlation statistics, with the difference being a direct consequence of the quantum statistics of light (it is bosonic) [2]. Jump forward to 2019, and Scott Bender from Utrecht University in the Netherlands and colleagues predict that similar correlation experiments in solid-state systems could reveal the coherence of magnons—magnetic excitations associated with electron spin [3]. The work by Bender et al. opens new experimental opportunities for the developing field of quantum magnonics, which seeks to duplicate the success of the more mature field of quantum optics but with magnons rather than photons.
Magnons can be thought of as waves that propagate through a lattice of spins, where wiggling one spin excites the motion of neighboring spins as a result of magnetic exchange interaction. Methods to generate and detect magnons have significantly improved in recent years, increasing the possibility that these collective excitations could soon find practical applications, such as the storage or transmission of information in computing [4]. Recent experiments have also hinted at the existence of a magnon Bose-Einstein condensate (BEC). In this system, magnons would propagate coherently in a single quantum state, offering a route to achieving dissipationless, spin-based information transfer via superfluid spin currents [5]. Currently, however, researchers lack a reliable and easily performed method for measuring the quantum coherence of a magnon BEC moving within a solid. This information would also be important in magnonics for understanding and utilizing magnon spin currents in applications beyond BECs.
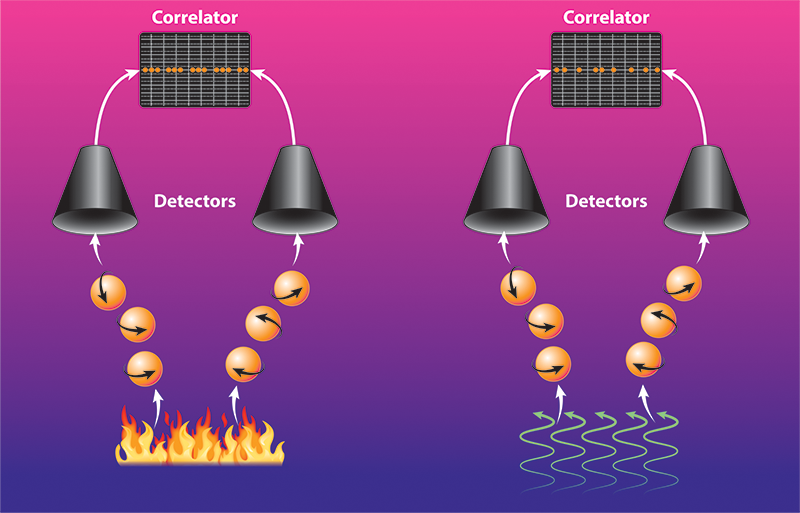
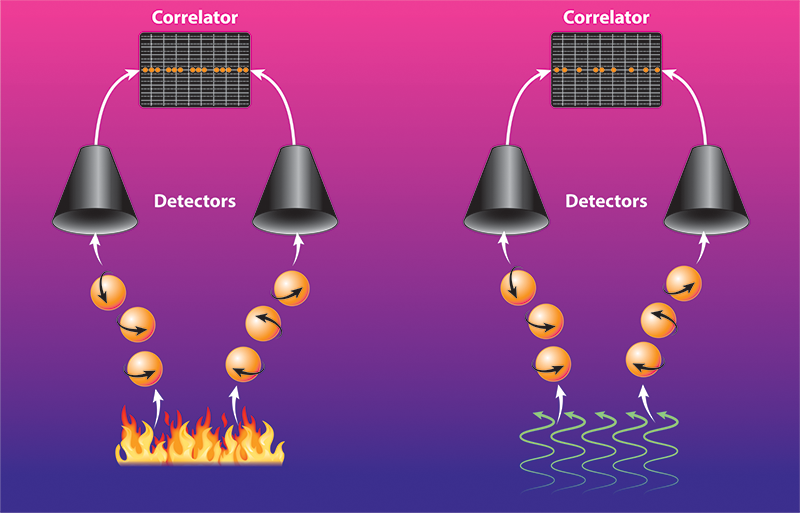
Bender and colleagues figured out how to get this information by adapting the approach invented by Hanbury Brown and Twiss, known as a cross-correlation experiment. As noted, an incoming light source is split into two beams, whose photons are measured at two separate photodetectors. The signals from these detectors are then used to determine the second-order correlation function g(2)(𝜏) of the two beams. This function describes the likelihood that a photon from one beam is counted on one detector a time 𝜏 after a photon from the other beam impacts the other detector. For a perfectly coherent light source, such as a laser, the photons in the two beams arrive at the detectors at random time intervals and g(2)(𝜏)=1, for all 𝜏. Photons from incoherent thermal light sources, such as blackbody radiation, however, typically arrive at the detectors in “bunches,” giving g(2)(0)>1. For single-photon sources, the photons “antibunch” and g(2)(0)<1—if a photon is directed down one beam to one detector, it is impossible to measure a photon at the second detector. (This behavior was observed in the 1970s by others utilizing the Hanbury Brown and Twiss technique.) Thus the coherence and nature of a light source can be judged by measuring g(2)(𝜏) using cross-correlation experiments. Bender and colleagues now predict that photon cross-correlation measurements can be adapted to magnons and used to detect the coherence of these excitations in ferromagnetic solids [3].
In their theoretical setup, the team replaces the light source with a magnon source and the photon detectors with two metal leads. The leads sit on top of a ferromagnetic material through which the magnons move, and these leads detect the magnon current by converting it into a charge current via the inverse spin Hall effect (Fig. 1). The detectors measure both the magnon current’s direction and intensity, which are then used to determine a metric similar to g(2)(𝜏) called c(2)(𝜏).
The team considers two well-known methods for generating magnons: coherent ferromagnetic resonance (FMR) and the spin Seebeck effect (SSE). In FMR, a resonant, time-varying magnetic field exerts a torque on the spins in the ferromagnet, which causes the spins to precess with a well-defined frequency and excites coherent magnons. In the SSE, a thermal gradient across the material leads to an excess of spin excitations on one side of the material. The resulting thermal magnons are incoherent, and they travel through the material via diffusion. The team’s calculations predict a bunching effect ( c(2)(0)>1) for magnons from thermal (SSE) sources and no bunching ( c(2)(0)=1) for magnons from coherent (FMR) sources. These predictions align with those for photons (blackbody vs laser).
Typically, methods to detect magnons generated by FMR or SSE involve measuring the dc voltage produced by the spin current that impinges on the metal leads. But such measurements average out any fluctuations in the signal, removing statistical effects that arise from the bosonic nature of the magnons. The detection technique proposed by Bender and colleagues solves this problem and could allow researchers to determine whether magnon coherence plays a role in determining a material’s spin transport properties, such as its behavior with respect to temperature or magnetic field [6].
An experimental realization of the team’s technique may be challenging because of the low sensitivity of present magnon detectors. There are also unsolved issues in spin current detection methods that relate to interfacial effects between the ferromagnetic material hosting the magnons and the metal leads. For photons, it took more than a decade from the experiments of Hanbury Brown and Twiss for scientists to create technology sensitive enough to detect antibunching [7]. A similar time frame may be needed to improve the sensitivity of current magnon detectors for future magnon cross-correlation measurements.
One exciting possible outcome of the proposed method is that it could be used to make cross-correlation measurements of any collective magnetic excitation that—like magnons—can be detected by the inverse spin Hall effect, including more exotic quantum collective excitations. For example, the technique could be used to probe the unconventional excitations of quantum magnets or quantum spin liquids. The quantum statistics of these excitations can be fermionic, bosonic, and even something in between (anyonic) [8, 9]. The concepts set forth by Bender and colleagues may therefore start a flurry of theoretical and experimental developments that could significantly push forward the still-evolving field of quantum magnonics.
This research is published in Physical Review Letters.
References
- R. Hanbury Brown and R. Q. Twiss, “Correlation between photons in two coherent beams of light,” Nature 177, 27 (1956).
- R. J. Glauber, “Coherent and incoherent states of the radiation field,” Phys. Rev. 131, 2766 (1963).
- S. A. Bender, A. Kamra, W. Belzi, and R. A. Duine, “Spin current cross-correlations as a probe of magnon coherence,” Phys. Rev. Lett. 122, 187701 (2019).
- V. V. Kruglyak, S. O. Demokritov, and D. Grundler, “Magnonics,” J. Phys. D. Appl. Phys. 43, 264001 (2010).
- D. A. Bozhko et al., “Supercurrent in a room-temperature Bose–Einstein magnon condensate,” Nat. Phys. 12, 1057 (2016).
- T. Kikkawa et al., “Critical suppression of spin Seebeck effect by magnetic fields,” Phys. Rev. B 92, 064413 (2015).
- H. J. Kimble, M. Dagenais, and L. Mandel, “Photon antibunching in resonance fluorescence,” Phys. Rev. Lett. 39, 691 (1977).
- D. Hirobe et al., “One-dimensional spinon spin currents,” Nat. Phys. 13, 30 (2016).
- H. Yao and D.-H. Lee, “Fermionic magnons, non-Abelian spinons, and the spin quantum Hall effect from an exactly solvable spin-1/2 Kitaev model with SU(2) symmetry,” Phys. Rev. Lett. 107, 087205 (2011).