The “Sound” of Weyl Fermions
Heat in a solid is mainly carried by lattice vibrations (phonons) and conducting electrons. These mechanisms of heat conduction are so dominant over other forms that in an ordinary material they are often assumed to be the only ones that matter. But as reported in a pair of papers, an exotic “vibration” of electrons might provide a third, significant way to conduct heat at low temperatures [1, 2]. This effect occurs in a family of materials called Weyl semimetals [3, 4], and it might be harnessed to guide heat through a material.
A Weyl semimetal is a material that hosts particles known as Weyl fermions. Originally conceived by German theoretician Herman Weyl in 1929 as a new type of fundamental particle with charge but no mass [5], a “true” Weyl fermion has never been observed in nature. But fermions that can be described by Weyl’s theory do appear as particle-like excitations (quasiparticles) in certain solids—namely, those with electron energy bands that are linear and cross at points (Weyl points) in momentum space near the Fermi energy [6–8]. Weyl points come in pairs that have opposite (+ or –) chirality. Electrons with momentum near to one of these points form quasiparticles with a similar chirality, where the + or – denotes whether the quasiparticle propagates parallel or antiparallel to its spin.
Because of this intrinsic chirality, Weyl quasiparticles behave differently than electrons in ordinary metals or semiconductors. Notably, they exhibit an unusual phenomenon called the chiral magnetic effect (CME), which occurs when a Weyl material is placed in a magnetic field [9]. Here, the field generates a current of + and – Weyl quasiparticles that move parallel and antiparallel to the field, respectively. In thermodynamic equilibrium, the net current is zero because + and – quasiparticles exist in equal numbers. But the balance is broken and a net quasiparticle current flows if one applies an electric field parallel to the magnetic field. This effect is dubbed the chiral anomaly because the number of particles with a given chirality isn’t conserved [10].
A signature of the chiral anomaly is negative magnetoresistance—a lowering of resistance with increasing magnetic field, which has been observed in Weyl materials by several groups. In one of the new papers, theorists Zhida Song and Xi Dai of the Hong Kong University of Science and Technology predict that the CME should also lead to a collective effect called chiral zero (CZ) sound [1]. Zero sound is a purely quantum-mechanical effect that was first proposed by Lev Landau in the context of Fermi-liquid theory [5] and later observed in helium-3. Like regular sound, zero sound comes from vibrations, but instead of air molecules, the vibrating “medium” is the momentum distribution of electrons near the Fermi level. Song and Dai have shown that zero sound vibrations exist in Weyl semimetals when the material is in a magnetic field.
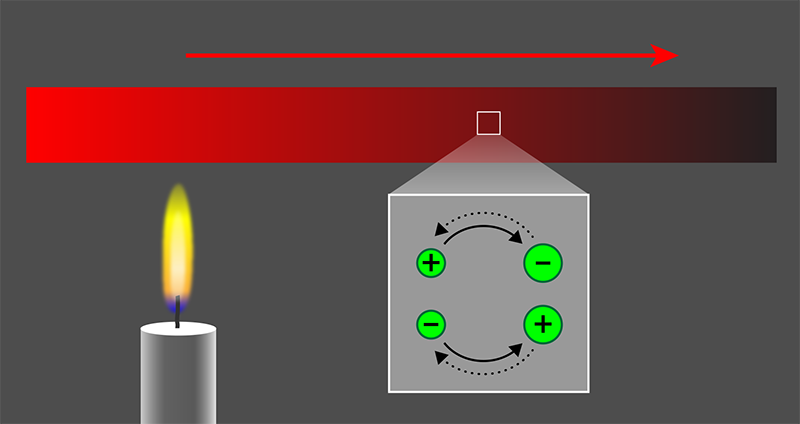
These vibrations are associated with some unusual effects in a Weyl semimetal with two or more pairs of Weyl points. If a temperature imbalance existed in a normal metal, electrons would move from the hot region to the cold one, carrying both heat and charge. A similar temperature gradient in a Weyl semimetal would cause CZ sound waves to flow from hot to cold. But these waves would only carry heat and no charge as they propagate through the material because of a sort of charge cancellation effect between Weyl-point pairs (Fig. 1). These heat-carrying waves can be excited with very little energy (their energy spectrum is gapless.) Therefore CZ sound waves can make a significant contribution to a material’s thermal conductivity. A CZ sound wave is also distinct from the zero sound wave conceived by Landau: it propagates only along the magnetic field direction, and its velocity is strongly modulated by this field. As Song and Dai explain in their paper, an experimental signature of a material that transmits CZ sound is that its specific heat and thermal conductivity can be controlled by a magnetic field.
In fact, Song and Dai’s work was inspired by a set of experiments from Peijie Sun of the Chinese Academy of Sciences in Beijing and colleagues [2]. The researchers, who reported their results in a 2018 preprint, had focused on TaAs, a Weyl semimetal with multiple pairs of Weyl points. The group had measured the material’s thermal conductivity and its electrical conductivity while ramping up the strength of an applied magnetic field. In metals, where conducting electrons dominate the thermal transport, the thermal and electrical conductivities are expected to oscillate up and down in a magnetic field; these oscillations occur because the field induces quantized energy levels (Landau levels) that move in and out of alignment with the Fermi level. Moreover, metals are expected to obey the Wiedemann-Franz law, which says that the thermal conductivity is proportional to the electrical conductivity multiplied by a fundamental constant and divided by the temperature.
Sun’s team, however, observed strikingly different behavior in TaAs. Analyzing the thermal conductivity along the direction of the magnetic field, they found that the thermal conductivity oscillated with an amplitude that was about 100 times greater than that predicted by the Wiedemann-Franz law. By contrast, the oscillation in thermal conductivity perpendicular to the field was much weaker. In addition, the team observed that the oscillations of the thermal conductivity and electrical conductivity were completely out of phase.
Through careful experiment, Sun and colleagues excluded several possible sources of the “giant” thermal conductivity oscillations, such as phonons and bipolar electron-hole excitations. They have now concluded that the most likely explanation is the CZ sound proposed by Song and Dai. In materials where this effect exists, a strong violation of the Wiedemann-Franz law is possible because heat and charge are no longer carried by the same particles.
Finding a new effect in solids is always intriguing to physicists. But the discovery of CZ sound might also have some practical value. In principle, one could use a magnetic field to guide (or block) the conduction of heat in a certain direction. That capability might, for example, allow heat to be routed around or away from some object—though the Weyl semimetal’s temperature has to be low enough for long-lived CZ sound waves, which for TaAs is below 10 K. In the immediate future, however, researchers are likely to look for CZ sound in the growing family of materials that contain Weyl points.
This research is published in Physical Review X and posted on the arXiv.
References
- Z. Song and X. Dai, “Hear the sound of Weyl fermions,” Phys. Rev. X. 9, 021053 (2019).
- J. Xiang et al., “Giant magnetic quantum oscillations and chiral anomaly in the thermal conductivity of a Weyl semimetal,” arXiv:1801.08457.
- N. P. Armitage, E. J. Mele, and Ashvin Vishwanath, “Weyl and Dirac semimetals in three-dimensional solids,” Rev. Mod. Phys. 90, 015001 (2018).
- B. Yan and C. Felser, “Topological materials: Weyl semimetals,” Annu. Rev. Cond. Mat. Phys. 8, 337 (2017).
- H. Weyl, “Elektron und gravitation. I,” Z. Phys. 56, 330 (1929).
- S. Murakami, “Phase transition between the quantum spin Hall and insulator phases in 3D: Emergence of a topological gapless phase,” New J. Phys. 9, 356 (2007).
- X. Wan, A. M. Turner, A. Vishwanath, and S. Y. Savrasov, “Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates,” Phys. Rev. B 83, 205101 (2011).
- A. A. Burkov and L. Balents, “Weyl semimetal in a topological insulator multilayer,” Phys. Rev. Lett. 107, 127205 (2011).
- K. Fukushima, D. E. Kharzeev, and H. J. Warringa, “Chiral magnetic effect,” Phys. Rev. D 78, 074033 (2008).
- H. B. Nielsen and M. Ninomiya, “The Adler-Bell-Jackiw anomaly and Weyl fermions in a crystal,” Phys. Lett. B 130, 389 (1983).