Coming Soon: Cold Atoms Impersonate Superconductors
Since their 1986 discovery, cuprate superconductors have puzzled physicists. These copper-containing materials can conduct electricity with zero resistance at temperatures of up to 135 K, well above the maximum temperature of 30 to 40 K predicted by theory. For the last 33 years, researchers have sought to explain this enigmatic behavior but still lack a complete description. However, physicists working with ultracold atoms arranged in ordered lattices of laser light think that their experiments could soon provide needed clues. These experiments may be close to generating a model of a high-temperature superconductor in which atoms play the role of electrons. Such a system would allow researchers unprecedented control over the factors that produce superconductivity and would provide a set of tools that could lead to a solution to the high-temperature mystery.
High-temperature superconductivity has been celebrated as a technology that could lead to cheaper high-speed trains and improved electricity generation in power plants. Those ideas have yet to pan out, although high-temperature superconductors have appeared in some devices that measure magnetic fields and in others that detect radar signals. Explaining high-temperature superconductivity in fundamental terms should help scientists optimize these materials. But the phenomenon is also arguably one of the biggest unsolved problems of condensed-matter physics. A complete theory of high-temperature superconductivity would provide new insights into the behaviors of electrons in solids.
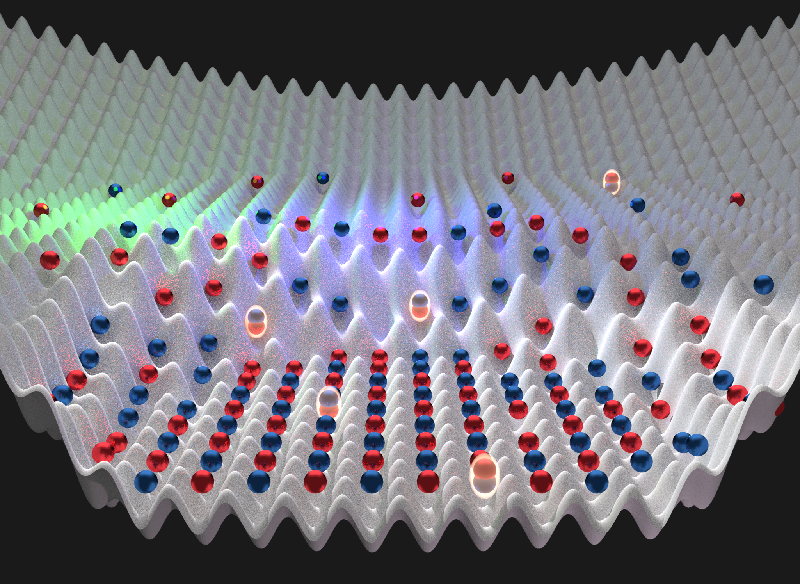
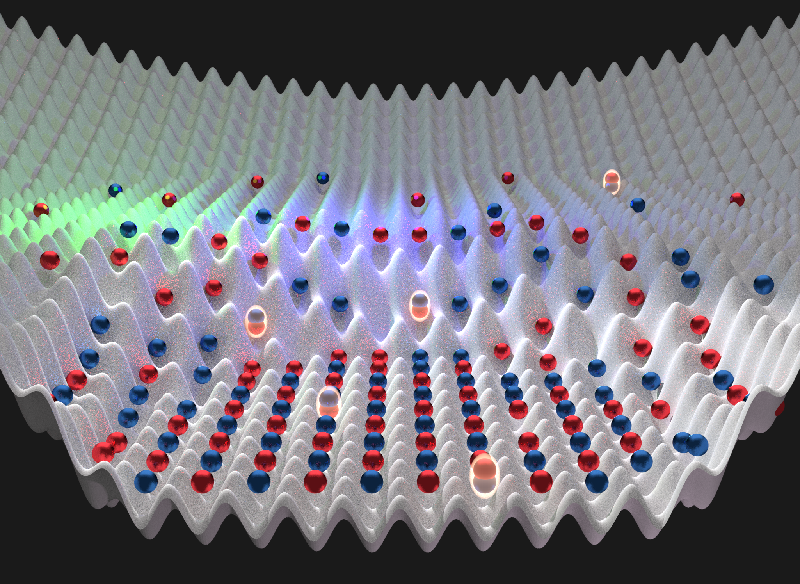
The problem in explaining the high-temperature superconductivity of cuprates comes from the complexity of the materials, which makes them hard to study via experiment, computer simulation, or pure theory. A simpler and more controllable model system could help, according to some researchers. Atoms with an odd number of neutrons are fermions and thus obey the same statistical rules as electrons (which are also fermions). And it turns out that such fermionic atoms, when cooled and placed in a crystal-like arrangement with lasers, can mimic the behaviors of electrons in a complex solid material. Atoms in such a lattice, for example, can hop from one site to the next like electrons moving through a crystal.
Superconductivity is just one example of the quantum states, or phases, that electrons can inhabit in materials. Experimentalists have very recently reproduced some of these other phases using lattices of fermionic atoms (fermion lattices). In the phase diagram for electronic states in cuprates, the observed fermion lattice phases border that of superconductivity, leading some experts to predict the imminent observation of a high-temperature superconducting state. This progress has come about in the last few years thanks to a surge in the development of tools for observing, cooling, and theoretically describing fermion lattices. “It has been a promise for a while that we could create the phases that condensed-matter [physicists] are excited about,” says Markus Greiner of Harvard University, a pioneer in the field of cold atom lattices. “But now, for the first time, we are actually realizing these phases experimentally.”
Quantum Gas Microscope
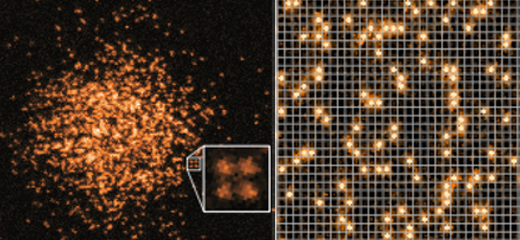
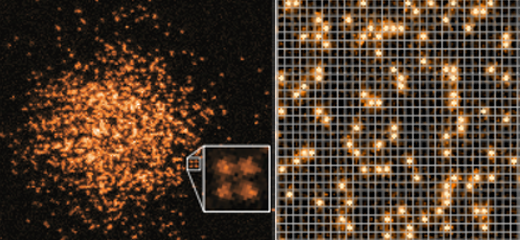
An initial stumbling block in studying lattices of cold fermions was an inability to image the atoms individually—a key requirement for investigating how the atoms arrange and interact at the single-atom level. The arrival of the quantum gas microscope (QGM) in 2009 changed that, although it was not until 2015 that researchers first imaged fermions using this technique [1–5]. (Before that they had only captured bosons, a different class of quantum particle.)
In QGM experiments, a magnetic or optical trap first confines a cloud of atoms in a small space, where the gas is cooled to nanokelvin temperatures using standard techniques. An optical lattice projected onto the cloud then traps and arranges the atoms in a periodic pattern. To probe this quantum state, the QGM uses a high-power objective lens to collect the fluorescent light emitted by the atoms.
“You can look at the individual sites in the lattice and image the number of atoms each site contains, as well as detecting the spins of the atoms,” says Waseem Bakr of Princeton University, New Jersey, who helped to build the first QGM. Bakr likens the technique to the scanning tunneling microscope (STM), which images solid materials at the atomic level, although he argues that the QGM has superior abilities. “With an STM you have to scan the material atom by atom, but with the quantum gas microscope you take a snapshot of the system, recording the entire [lattice] at a particular instant.”
The Fermi-Hubbard Model
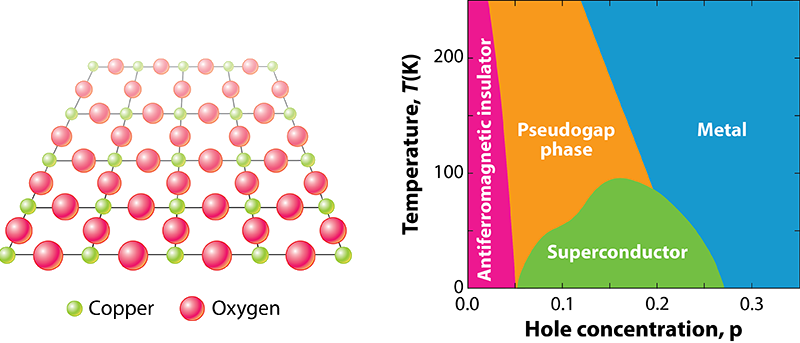
To interpret their QGM images, physicists use the so-called Fermi-Hubbard model, the simplest model of interacting fermions in a lattice. Despite its simplicity, researchers expect that the idealized material described by the model will exhibit several electronic phases, including superconductivity, so they have worked hard to understand this model and its predictions. Many believe that the Fermi-Hubbard model accurately describes interacting electrons in cuprates, although that remains unconfirmed, says Martin Zwierlein, who carries out cold-atom experiments at the Massachusetts Institute of Technology, Cambridge. In the model, fermions can jump between sites arranged in a 2D square lattice. In cuprates, the copper and oxygen atoms form a similar 2D lattice, and the 3D structure is made from stacks of these layers alternating with layers containing other elements. Electrons move between copper ions via the oxygen bonds.
For 2D lattices, theorists can solve the Fermi-Hubbard model numerically (through computer simulation) when exactly one atom sits in each lattice site or when the temperature is “high”—well above that expected for the superconducting phase. Otherwise the model is largely intractable, despite theorists making some recent progress, says Andrew Daley of the University of Strathclyde in the UK, a theorist who studies ultracold quantum gases. On the other hand, experiments don’t have the same limitations as computers, so a lattice of ultracold fermions is an ideal means to “simulate” and explore the Fermi-Hubbard model’s predicted phases, once experimental challenges are overcome, Daley says. This sentiment is echoed by Christie Chiu of Harvard University, who works with Greiner. “If you want to [experimentally] simulate cuprate materials with cold atoms, then the Fermi-Hubbard model is your foundation,” she says.
Until recently, experiments were limited to studying phases such as the Mott insulator, which exists at temperatures well above that of the elusive superconductor. Then, two years ago, Greiner, Chiu, and colleagues, used a QGM to create and image an antiferromagnet, a phase in which one atom occupies each lattice site, and the spins of neighboring atoms point in opposite directions [6]. “Crudely speaking, if you take a snapshot of the atoms, you see checkerboard ordering of the spins,” Bakr says. Around the same time, others performed similar demonstrations of the antiferromagnetic phase, albeit over a smaller number of atoms [7–10].
A few months ago, Bakr and his team observed another phase: the strange metal, a mysterious metallic phase with poor electrical conductance [11]. Researchers are also beginning “doping” experiments, where empty lattice sites—“holes”—are created in the antiferromagnet. Creating holes could allow them to explore the so-called pseudogap phase, which involves analogous holes among the electrons in a material [12].
If you plot temperature versus the density of fermions (or holes) to make a phase diagram for cuprates, then the antiferromagnet, strange metal, and pseudogap phases all neighbor the superconducting phase. Observations of some of these phases in fermion lattices has led to anticipation that a superconductor will be spotted next. “These phases are believed to be precursors to high-temperature superconductivity in cuprates,” says Lindsay LeBlanc, from the University of Alberta in Canada, who carries out ultracold-atom experiments.
Experiments have made “huge progress” in the last year, says Ana Maria Rey, a cold-atom theorist at JILA in Colorado. She says the experiments are “very close”—a year or two away at most—to realizing a high-temperature superconductor. Greiner agrees. “If there is such a phase, it’s only a matter of time before we get to it.”
No Ice Bucket for Fermions
The recent progress stems in large part from tricks researchers are developing to cool their fermion lattices to ever lower temperatures. The temperature in these experiments routinely drops to tens of nanokelvin, but even under such frosty conditions, the atoms still have significant thermal energy. Electrons having similar energies would be at temperatures around 1000 K, well above that needed for superconductivity to develop. “These ultracold experiments are not that cold in a relative sense,” LeBlanc says. “Making things cold is always difficult. You have to put that energy and entropy somewhere, and that becomes harder and harder to do in these isolated cold-atom systems that we work with in the laboratory.”
Traditionally, objects are cooled by putting them in contact with a colder body, which acts as a heat sink, sucking out the object’s energy. For Joseph Thywissen of the University of Toronto, who studies fermion lattices, the go-to example for this cooling method is a champagne bottle in an ice bucket, where the ice acts as the heat sink. “But there is no ice bucket we can use to cool a 10-nanokelvin cloud [of atoms] down to 2 nanokelvin,” he says. Instead, researchers are trying out other methods.
For Greiner’s team, the trick to cooling the atoms enough to make the antiferromagnetic phase involved redistributing energy within the lattice, with atoms on the outer edges acting as the heat sink. By doing this, the team reduced the energy of the atoms at the lattice’s center by more than a factor of 2 over the previous best. Other groups are trying out related methods to shuffle energy around, but no further temperature reductions have yet been seen.
“Experiments have been making enormous progress in the temperatures that they can reach” over the past 10 years, says Emanuel Gull, a condensed-matter theorist at the University of Michigan in Ann Arbor, although he remains skeptical that fermion lattices will prove useful for simulating and understanding a high-temperature superconductor. “None of the experiments so far reaches a regime where you can answer questions about cuprates, because the temperature is still way too high,” he says.
Most experts agree that an additional fivefold drop in temperature is needed for experiments to reach the superconducting phase. Although Harvard experimentalist Chiu admits, “we don’t really know how low we need to go.” But even without realizing this mysterious phase, the experimental advances that achieved the phases observed so far are allowing researchers to enter regimes that are inaccessible to computer simulations, which could potentially allow them to uncover new behaviors. “For the first time we have this quantum Lego [set] that we can really tinker with and build new things,” Greiner says.
Observing a Superconductor Is Just the Start
The possibility of a quantum Lego set has many excited, including Daley and others who are beginning to use fermion lattices to study properties of materials. “When we started out, the experiments were all about trying to reproduce the phases that condensed-matter theorists had already thought about,” he says. “Now there are serious endeavors to use fermions in optical lattices, and other cold atom systems, as simulators for materials science and to go beyond already conceived condensed-matter problems.” Gull thinks that the potential benefits of fermion lattices lie in studying dynamical problems, where one observes the state of the lattice evolving over time. “[Dynamics] is something that none of the numerical methods can probe. We don’t have the tools,” he says. “That is where we can really go and play.”
For many, however, realizing a cold-atom superconductor remains the ultimate goal—at least for now. But even when they achieve that goal, researchers will still have many steps to take before they might uncover the long-standing mystery of the cuprates’ high-temperature superconducting abilities. “Simulation is not the same thing as understanding,” Thywissen says. “If we realize a superconductor with cold atoms, then we will need to design specific experiments and pose carefully chosen questions to unravel the physical mechanisms behind the phenomenon observed.” Simulating a high-temperature superconductor, he says, “is not the end of the story, it’s just the beginning.”
–Katherine Wright
Katherine Wright is a Senior Editor for Physics.
References
- W. S. Bakr, J. I. Gillen, A. Peng, S. Fölling, and M. Greiner, “A quantum gas microscope for detecting single atoms in a Hubbard-regime optical lattice,” Nature 462, 74 (2009).
- M. F. Parsons, F. Huber, A. Mazurenko, C. S. Chiu, W. Setiawan, K. Wooley-Brown, S. Blatt, and M. Greiner, “Site-resolved imaging of fermionic 6Li in an optical lattice,” Phys. Rev. Lett. 114, 213002 (2015).
- L. W. Cheuk, M. A. Nichols, M. Okan, T. Gersdorf, V. V. Ramasesh, W. S. Bakr, T. Lompe, and M. W. Zwierlein, “Quantum-gas microscope for fermionic atoms,” Phys. Rev. Lett. 114, 193001 (2015).
- E. Haller, J. Hudson, A. Kelly, D. A. Cotta, B. Peaudecerf, G. D. Bruce, and S. Kuhr, “Single-atom imaging of fermions in a quantum-gas microscope,” Nat. Phys. 11, 738 (2015).
- G. J. A. Edge, R. Anderson, D. Jervis, D. C. McKay, R. Day, S. Trotzky, and J. H. Thywissen, “Imaging and addressing of individual fermionic atoms in an optical lattice,” Phys. Rev. A 92, 063406 (2015).
- A. Mazurenko, C. S. Chiu, G. Ji, M. F. Parsons, M. Kanász-Nagy, R. Schmidt, F. Grusdt, E. Demler, D. Greif, and M. Greiner, “A cold-atom Fermi–Hubbard antiferromagnet,” Nature 545, 462 (2017).
- M. Boll, T. A. Hilker, G. Salomon, A. Omran, J. Nespolo, L. Pollet, I. Bloch, and C. Gross, “Spin- and density-resolved microscopy of antiferromagnetic correlations in Fermi-Hubbard chains,” Science 353, 1257 (2016).
- M. F. Parsons, A. Mazurenko, C. S. Chiu, G. Ji, D. Greif, and M. Greiner, “Site-resolved measurement of the spin-correlation function in the Fermi-Hubbard model,” Science 353, 1253 (2016).
- L. W. Cheuk, M. A. Nichols, K. R. Lawrence, M. Okan, H. Zhang, E. Khatami, N. Trivedi, T. Paiva, M. Rigol, and M. W. Zwierlein, “Observation of spatial charge and spin correlations in the 2D Fermi-Hubbard model,” Science 353, 1260 (2016).
- P. T. Brown, D. Mitra, E. Guardado-Sanchez, P. Schauss, S. S. Kondov, E. Khatami, T. Paiva, N. Trivedi, D. A. Huse, and W. S. Bakr, “Spin-imbalance in a 2D Fermi-Hubbard system,” Science 357, 1385 (2017).
- P. T. Brown et al., “Bad metallic transport in a cold atom Fermi-Hubbard system,” Science 363, 379 (2018).
- C. S. Chiu, G. Ji, A. Bohrdt, M. Xu, M. Knap, E. Demler, F. Grusdt, M. Greiner, and D. Greif, “String patterns in the doped Hubbard model,” arXiv:1810.03584.